

隐马尔可夫模型描述一个含有隐含未知参数的马尔可夫过程
电子说
描述
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来作进一步的数据分析,例如模式识别。
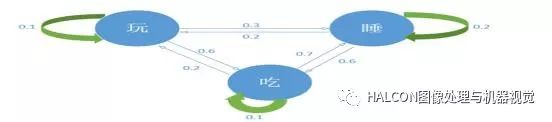
HMM在建模的系统被认为是一个马尔可夫过程与未观测(隐藏的)到状态的统计马尔可夫模型。一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态之间存在转换概率。
可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个做输出概率。如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。

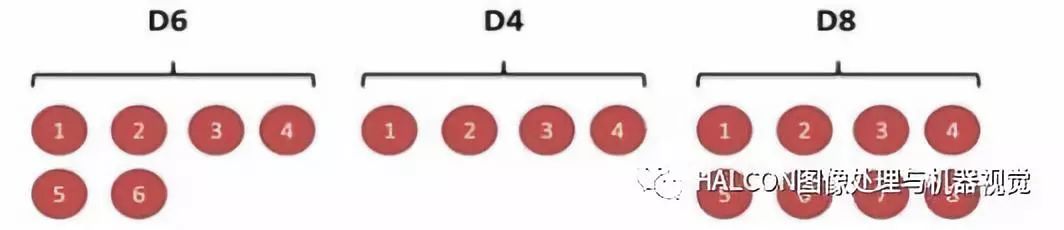
通过下图骰子例子说明:第一个骰子是我们平常见的骰子(称骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。第二个骰子是个四面体(称骰子为D4),每个面(1,2,3,4)出现的概率是1/4。第三个骰子有八个面(称骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
HMM模型相关的算法主要分为三类:
1、知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。这个问题有两种解法,给出两个不同的答案。

第一种解法求最大似然状态路径,说通俗点呢,就是求一串骰子序列,这串骰子序列产生观测结果的概率最大。第二种解法,就不是求一组骰子序列了,而是求每次掷出的骰子分别是某种骰子的概率。
2、知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。看似这个问题意义不大,因为掷出来的结果很多时候都对应了一个比较大的概率。

问这个问题的目的呢,其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率,那么就说明我们已知的模型很有可能是错的,有人偷偷把我们的骰子給换了。
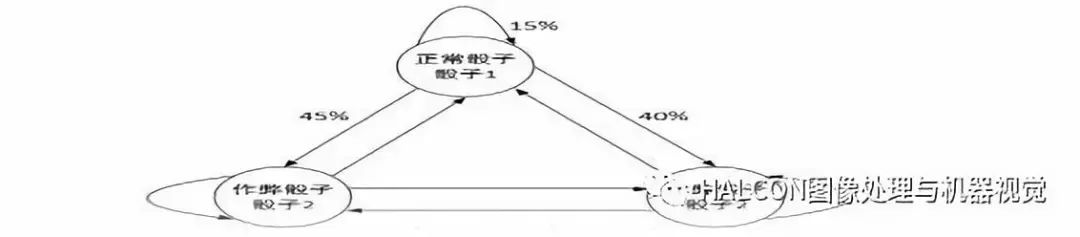
3、知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。

这是最常见的情况,很多时候我们只有可见结果,不知道HMM模型里的参数,我们需要从可见结果估计出这些参数,这是建模的一个必要步骤。

比如说怀疑自己的六面骰被赌场动过手脚了,有可能被换成另一种六面骰,这种六面骰掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。怎么办么?答案很简单,算一算正常的三个骰子掷出一段序列的概率,再算一算不正常的六面骰和另外两个正常骰子掷出这段序列的概率。如果前者比后者小,就要小心了。比如说掷骰子的结果是:

要算用正常的三个骰子掷出这个结果的概率,其实就是将所有可能情况的概率进行加和计算。同样,简单而暴力的方法就是把穷举所有的骰子序列,还是计算每个骰子序列对应的概率,把所有算出来的概率相加,得到的总概率就是我们要求的结果。解决这个问题的算法叫做前向算法,如果我们只掷一次骰子:

看到结果为1,产生这个结果的总概率可以按照如下计算,总概率为0.18:

把这个情况拓展,我们掷两次骰子:

看到结果为1,6.产生这个结果的总概率可以按照如下计算,总概率为0.05:

继续拓展,我们掷三次骰子:

看到结果为1,6,3,产生这个结果的总概率可以按照如下计算,总概率为0.03:

同样的,我们一步一步的算,有多长算多长,再长的马尔可夫链总能算出来的。用同样的方法,也可以算出不正常的六面骰和另外两个正常骰子掷出这段序列的概率,然后我们比较一下这两个概率大小,就能知道你的骰子是不是被人换了。

-
基于隐马尔可夫模型的音频自动分类2011-03-06 1858
-
基于概率的统计分析隐马尔可夫模型2019-08-20 905
-
隐马尔可夫模型的组成2019-10-14 1691
-
基于隐马尔可夫模型的火焰检测2009-04-14 1031
-
用隐马尔可夫模型设计人脸表情识别系统2009-05-14 906
-
基于隐马尔可夫的系统入侵检测方法2009-08-05 638
-
隐马尔可夫模型(HMM)攻略(有具体例子-方便理解)2016-12-07 1163
-
基于改进的隐马尔可夫模型的态势评估方法2017-12-03 863
-
基于隐马尔可夫模型的短波认知频率选择方法2017-12-18 1050
-
基于隐马尔可夫模型的软件状态评估预测方法2018-01-05 964
-
基于隐马尔可夫预测的功率博弈机制2018-02-02 1090
-
基于耦合多隐马尔可夫模型人体动作识别2018-03-29 1121
-
关于时间连续的马尔可夫过程的详细解说2018-04-20 762
-
人工智能之马尔可夫模型(MM)概述2018-05-29 11272
-
基于隐马尔科夫模型的公交乘客出行链识别2021-07-02 747
全部0条评论

快来发表一下你的评论吧 !

