

大学里好不容易听懂的统计学,会变成一件没“意义”的事情吗?
电子说
描述
三位统计学家在Nature上发布公开信,号召科学家放弃追求“统计学意义”,这封公开信一周之内吸引了超过800名研究人员共同签署。大学里好不容易听懂的统计学,会变成一件没“意义”的事情吗?
统计学白学了?
最新一期Nature杂志发表了三位统计学家的一封公开信,他们号召科学家放弃追求“统计学意义”,并且停止用统计学中常见的P值作为判断标准。
一般认为P≤0.05或者P≤0.01就有显著性差异,研究就有统计意义。
统计学上无显著的结果并不能“证明”零假设;统计上显著的结果也没有“证明”某些其他假设。事实真的是这样吗?
他们的这篇文章名为《科学家们起来反对统计学意义》(Scientists rise up against statistical significance)。

标题犹如战斗檄文一样令人振奋。在文章发出不到24小时,就有250多人签名支持,一周之内吸引了超过800名研究人员共同反对。
大学里好不容易听懂的统计学,会变成一件没“意义”的事情吗?
为什么要放弃统计学意义的概念?
几代人以来,研究人员一直被警告说:统计上不显著的结果并不能“证明”零假设(即假设各组之间没有差异,或者某个处理方法对某些测量结果没有影响)。统计上显著的结果也不能“证明”其他一些假设。这种误解用夸大的观点扭曲了文献,而且导致了一些研究之间的冲突。
因此,三位统计学家提出一些建议,让科学家们不至于成为这些误解的牺牲品。
首先明确必须停止的事:永远不应该仅仅因为P值大于阈值(如0.05)就得出“没有差异”或“没有关联”的结论;或者,仅仅因为置信区间包含0就得出这样的结论。
同时,我们也不应该断定两项研究之间存在冲突,只因为其中一项研究的结果具有统计学意义,而另一项则没有。这些错误浪费了研究工作,误导了政策决策。
例如,考虑一系列对消炎药意外效果的分析。由于他们的研究结果在统计学上不显著,一组研究人员得出结论说:暴露在这些药物中与新发房颤(最常见的心律紊乱)“无关”,并且这些结果与之前的一项研究结果相反,而之前的研究结果具有统计学意义。
现在,让我们看看实际的数据。研究人员描述了他们的统计不显著的结果,发现风险比为1.2。他们还发现95%的置信区间跨越了从微不足道的风险降低3%到非常显著的风险增加48%(P = 0.091)。研究人员从较早的具有统计学意义的研究中发现,风险比同样为1.2。这项研究更加精确,其风险区间在9%到33%之间(P = 0.0003)。
当区间估计包含严重的风险增加时,得出结论认为统计上不显著的结果显示“无关联”是荒谬的;同样荒谬的是,声称这些结果与先前研究中显示相同观察效果的结果相反。然而,这些常见的实践表明,依赖统计意义上的阈值会误导我们。
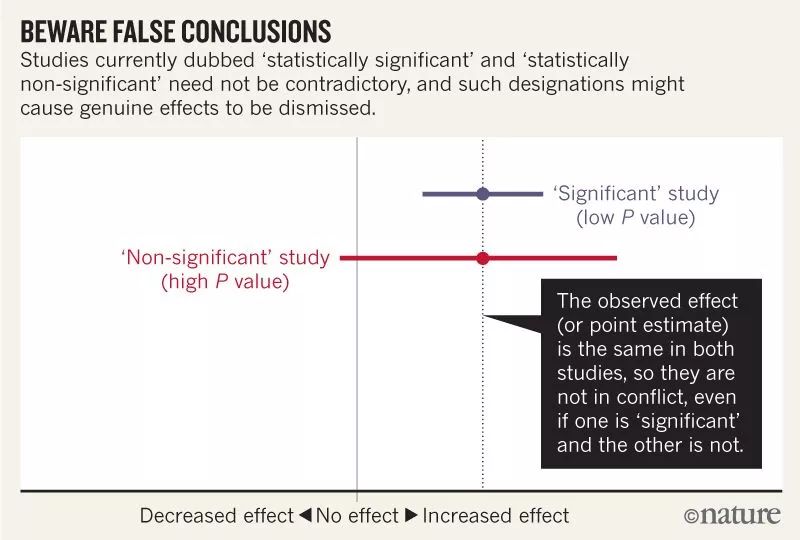
谨防错误结论
这些错误以及类似的错误普遍存在。对数百篇文章的调查发现,统计上不显著的结果被解释为“没有差异”或“没有影响”的约有一半。
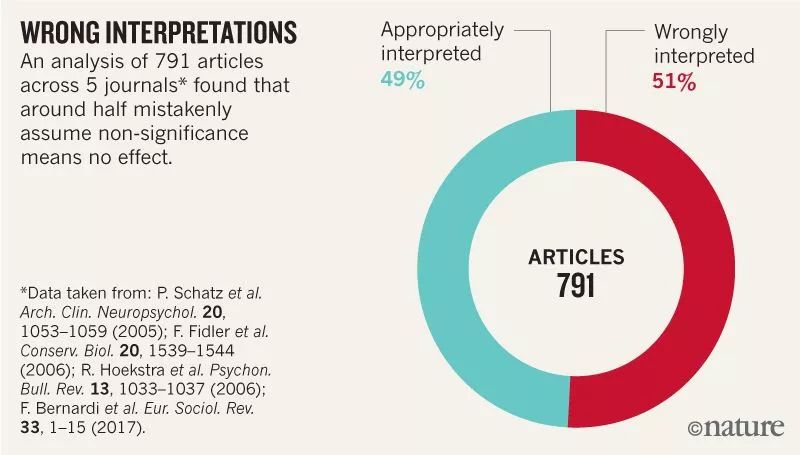
2016年,美国统计协会在《美国统计学家》上发表声明,警告误用统计意义和P值。本月,《美国统计学家》杂志又发表了40多篇关于“21世纪的统计推断:一个没有P<0.05的世界”的论文。编辑们在介绍这期特刊的时候谨慎地说,“不要说’统计意义重大’”。

《美国统计学家》杂志最新报道
三位统计学家也同意这一点,并呼吁放弃整个统计意义的概念。
停止使用非黑即白的P值,800多研究者同意
这三位统计学家写完《科学家们起来反对统计学意义》(Scientists rise up against statistical significance)一文草稿之后,邀请了其他人阅读,并表示如果人们同意三人的观点,就签上自己的名字。
没想到这篇文章得到了诸多人的赞同,在最初的24小时内,就有250人签了名。一星期后,共收到800多份签名,签名者包括来自50多个国家的统计学家、临床和医学研究人员、生物学家和心理学家,除南极洲没人以外,所有大洲都有人签名。
一名倡导者称,这是“对统计意义轻率测试的外科手术式打击”,也是“一个为更好的科学实践发声的机会”。
同时,三位统计学家也强调,他们不是在呼吁禁止P值。不是说P值不能在某些特定的应用程序中用作决策标准,而是他们与过去几十年的许多其他研究结果一样,呼吁停止以传统的二分法使用P值——来决定结果是反驳还是支持一项科学假设。
避免这种“二分法”的一个原因是,所有的统计数据,包括P值和置信区间,都会随着研究的不同而自然地发生变化,并且往往变化非常大。事实上,单凭随机变化就能很容易导致P值的巨大差异,远远不止落在0.05阈值的任何一侧。例如,即使研究人员可以对一些真实的效果进行两次完美的复制研究,每次都有80%的机会达到P < 0.05,那么其中一个得到P < 0.01,另一个得到P > 0.30也就不足为奇了。无论P值是大是小,都需要谨慎。
问题不在于统计,而在于人和认知:把结果分成“统计显著性”和“统计非显著性”,让人们认为以这种方式分配的项目是截然不同的。同样的问题也可能出现在任何涉及二分法的统计替代方法中,无论是频域法、贝叶斯法还是其他方法。
不幸的是,科学家和期刊编辑们错误地认为,超过统计意义的临界值就足以证明一个结果是“真实的”,这导致他们对这类结果给予了特权,从而扭曲了文献。统计上有意义的估计值在大小上向上偏倚,而且可能偏差的幅度很大,而统计上不显著的估计值是向下偏倚的。
因此,任何侧重于统计学意义的估计的讨论都是有偏见的。最重要的是,对统计意义的严格关注鼓励研究人员选择一些数据和方法,这些数据和方法对于某些期望的结果具有统计显著性(或者仅仅是可发表的),或者对于不期望的结果没有统计显著性,例如药物的潜在副作用,从而使结论无效。
预先登记研究和承诺公布所有分析的所有结果可以大大减轻这些问题。然而,即使是预先登记的研究结果也可能因分析计划中始终未作决定而产生偏差。即使是出于好意,这也会发生。
放弃了统计学意义,我该怎么办?
Nature在2014年的一篇文章中,讨论了P值并不像许多科学家所假设的那样可靠,当时文章引起了业界很大反响,由此引发了后来美国统计协会在2016年警告滥用统计意义和P值。
如果研究人员确实放弃了统计学意义,他们应该做些什么呢?
三位统计学家认为:我们必须学会接受不确定性。
一种实用的方法是将置信区间重新命名为“兼容区间”(compatibility intervals),并以避免过度自信的方式解释它们。具体地说,建议作者描述区间内所有值的实际含义,特别是观察到的效果和极限。在这样做时,他们应该记住,考虑到用来计算区间的统计假设,区间极限之间的所有值都与数据合理地兼容。因此,在区间中挑出一个特定的值(例如null值)没有任何意义。
当谈到兼容间隔时,请记住四件事:
首先,仅仅因为区间给出了与数据最相容的值,在给定假设条件下,并不意味着区间外的值是不相容的;它们只是兼容性较差。事实上,区间外的值与区间内的值没有本质上的区别。因此,说区间表示所有可能的值是错误的。
其次,根据假设,并不是所有的值都与数据一致。点估计值(point estimate)是最兼容的,接近它的值比接近极限的值更兼容。这就是为什么我们敦促作者讨论点估计,即使他们有一个大的P值或一个大的区间,以及讨论该区间的极限。
第三,与0.05的阈值一样,用于计算区间的默认95%本身也是一种任意约定。它基于这样一种错误的想法,即计算出的区间本身有95%的几率包含真实值,同时还有一种模糊的感觉,即这是一个自信决策的基础。根据应用程序的不同,可以调整不同的级别。而且,就像在抗炎药物的例子中一样,如果把区间估计施加的二分法当作一种科学标准来对待,区间估计可能会使统计显著性的问题长期存在。
最后,也是最重要的一点,要谦虚:兼容性评估取决于用于计算区间的统计假设的正确性。在实践中,这些假设受制于相当大的不确定性。使这些假设尽可能清晰,并测试你可以测试的假设,例如通过绘制数据并拟合替代模型,然后报告所有结果。
无论统计数据显示什么,都可以为你的结果提出理由,但要讨论一系列可能的解释,而不仅仅是你喜欢的那些。推论应该是科学的,而不仅仅是统计的。背景证据、研究设计、数据质量和对潜在机制的理解等因素往往比P值或区间等统计度量更重要。
同时,三位统计学家呼吁消除统计意义,并将置信区间作为兼容性区间,这并不是万灵药。尽管它将消除许多不好的实践,但它很可能引入新的问题。因此,监测文献中的统计滥用应该是科学界目前的一项优先事项。
但是,当原始研究和复制研究的结果高度一致时,消除分类将有助于阻止过分自信的断言、“没有区别”的不合理声明和关于“复制失败”的荒谬声明。滥用统计意义对科学界和那些依赖科学建议的人造成了很大的危害。P值、区间和其他统计度量都有它们的位置,但现在是统计意义消失的时候了。
这也并不意味着大学的统计学白上了。研究人员可以从教育自己对统计的误解开始,最重要的是在每项研究中从多个角度考虑不确定性。从逻辑、背景知识和实验设计应与P值和类似指标一起考虑,以得出结论并确定其确定性。
在确定使用哪种方法时,研究人员还应尽可能地关注实际问题。对于使用统计数据的最佳方式而言,在抽象理论上给予否定的人,在提出具体情景时,往往会给予肯定的结果。
简而言之,要持怀疑态度,选择一个好问题,并尝试以多种方式回答它。毕竟,接近事实需要很多数字。
最后,介绍一下这三位统计学家。
Valentin Amrhein,瑞士巴塞尔大学的动物学教授;
Sander Greenland,加州大学洛杉矶分校的流行病学和统计学教授;
Blake McShane,伊利诺伊州埃文斯顿西北大学的统计学方法学家和营销学教授。
-
哎,生活不容易啊2012-03-29 3000
-
一款笔记本电脑电路图。好不容易搞到的。2012-07-12 9081
-
好不容易找到的Matlab基础及其应用教程(超高清中文版)2013-01-08 49976
-
精品:CAM350拼板个人总结 ,好不容易才整理出来的2013-05-03 15154
-
统计学和编程题目2019-09-10 1542
-
统计学的概率分布2019-09-27 1016
-
有没有用过SHT20的同学,我好不容易调通了,但数据误差较大怎么破?2020-08-21 3548
-
如何使用统计学知识进行和统计分析误差分析?2018-08-22 5717
-
人工智能其实就是华丽的统计学?2018-08-13 3281
-
人工智能只有统计学吗2019-10-14 1378
-
统计学对于机器学习有什么作用2020-04-05 1825
-
深度学习与经典统计学的差异2022-09-20 1780
全部0条评论

快来发表一下你的评论吧 !

