一种基于场路结合、对具有屏蔽机壳的电子设备进行系统级电磁敏感性仿真分析的新方法.

摘要: 提出了一种基于场路结合、对具有屏蔽机壳的电子设备进行系统级电磁敏感性(EMS)仿真分析的新方法. 该方法采用有限元法计算外部电场分布, 对电场沿固定路径积分, 得到所需的表面干扰电压, 将外部电磁干扰对内部电路的影响等效为电压源的作用, 再利用基于电路模型和全波分析相结合的方法对内部高速电路进行EMS 仿真分析, 弥补了以往在EMS 分析时只以实验为主,缺乏理论依据的缺陷. 实例仿真分析表明, 该方法简单、直观, 不仅可以详细分析电子设备内部高速电路中干扰的传播情况, 而且可以对内部高速电路进行优化设计, 提高了系统的抗干扰性.

近年来, 由于电子设备的集成化和高速化, 加剧了印刷电路板(PCB)上连接线的传输线效应, 增大了电路间的互相干扰, 降低了电子设备受干扰信号的幅值和能量, 从而使得电子设备的电磁敏感性(EMS)问题变得越来越突出. 因此, 对电子设备的电磁敏感性进行仿真分析具有重要的理论和实用价值.

电子电路通常总是罩着金属屏蔽机壳以减少周围环境对电子电路的干扰, 然而机壳并不总是密封的, 周围的电磁干扰会通过孔、槽和连接线这样一些耦合通道进入电子设备内部的敏感器件, 影响其正常工作, 而对于大多数的电子设备, 连接在机壳外部的信号线和电源线是引进外部干扰的主要通道之一. 因此, 研究带有屏蔽机壳和外部电缆的电子设备的电磁敏感性具有普遍意义.

目前, 人们已经在电子设备印刷电路板(PCB)的EMS 方面做了大量的仿真研究工作[ 1-9] , 但针对电子设备系统级的EMS 方面的仿真研究工作在国外还只是刚刚起步, 国内至今还未见文献报道. 参考文献[ 10] 首次提出了利用矩量法(MOM)计算流过信号线与机壳结合点处的感应电流, 将外部电磁干扰对内部电路的影响等效为由短路电流和等效电阻组成的等效源模型的思想, 并将其方法应用于多层PCB 板连接线的EMS 分析中. 参考文献[ 11] 又将上述方法扩充到具有集成电路插件的多层PCB 板的EMS 仿真分析中. 但是, 由于电子设备的实际使用环境以及信号线与机壳内部电路连接方式的差别, 究竟应该如何计算外部电磁干扰, 以及如何等效外部电磁干扰对内部电路的影响, 还有待于进一步研究. 

本文在对被屏蔽的电子设备的EMS 进行分析时, 提出了采用有限元法计算外部电场分布, 将外部电磁干扰对内部电路的影响等效为电压源的方法, 在此基础上采用基于电路模型和全波分析相结合的方法对内部高速电路进行了EMS 仿真分析,并对内部高速电路进行了优化设计.

1 　方法描述本文在对电子设备进行系统级电磁敏感性分析时将其分为内外两个区域, 外部区域由屏蔽机壳和信号线组成, 内部区域由内部高速电路组成, 如图1所示. 具体方法如下:

①利用有限元法仿真被平面电磁波干扰照射的外部屏蔽机壳和信号线, 计算电场分布, 将其电场沿固定路径积分得到信号线与机壳结合处的表面干扰电压, 此干扰电压即为内部高速电路的输入噪声源;

②采用传统的基于电路的模型、描述器件外部特性的IBIS(Input /output Buf fer Informatio n Specification)模型以及传输线的分布模型和全波模型来建立由PCB 板上的连接线、分立元件和集成电路(IC)插件组成的内部高速电路的仿真模型;

③将第①步计算得到的表面干扰电压作为第②步得到的内部高速电路仿真模型的输入, 分析由信号线耦合的输入噪声对内部高速电路的影响;

④对内部高速电路进行优化设计, 使其对输入噪声的敏感程度达到最低.

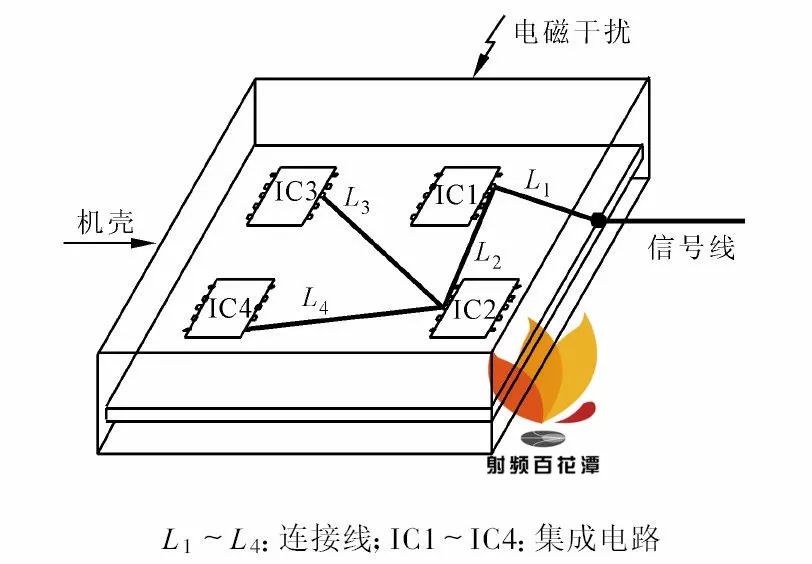
图1　电子设备结构图

1. 1 　利用电磁场理论计算外部干扰电压源

首先假设电子设备周围的电磁干扰为均匀平面谐波, 且有

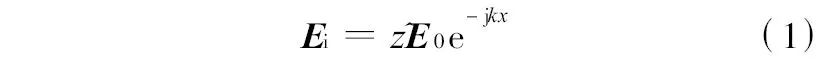
式中:Ei 表示入射电场;E0 是入射电场幅度;k 是传播常数;^z 是谐波的传播方向.

由于假设屏蔽机壳为理想导体, 因此电磁波不可能穿透导体, 而只是入射到机壳表面上感应出表面电流. 现假设由感应电流产生的散射电场为Es ,机壳表面的法向量为^n , 则在机壳表面上应用边界条件^n ×(Ei +Es)=0 , 可得到机壳表面切线方向的散射电场为

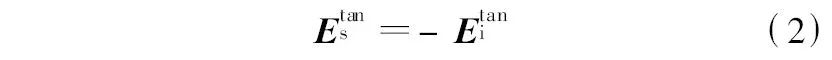
而对于时谐电磁场而言, 在均匀、线性、各向同性、无源以及不导电的媒质区域中, 根据麦克斯韦方程组可得到如下表达式

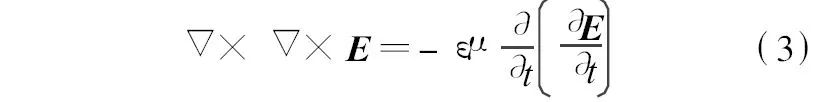
式中:ε、μ分别为周围媒质的介电常数和磁导率.时谐电场表达式为

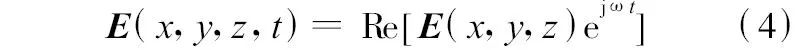
于是, 可得到假设为均匀平面谐波的电磁干扰在传播过程中满足的关系式为

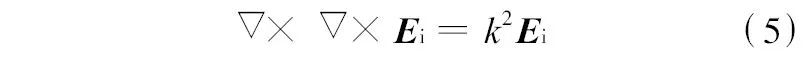
式中:传播常数k =ω(με)12. 由(2)式知, 机壳表面的散射场应满足边界条件

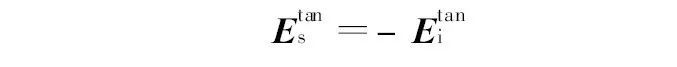
因此, 求解式(5)就可得到机壳表面散射场的电场分布. 本文利用Ansof t HFSS 软件求解该散射场. 在应用Ansof t HFSS 软件求解式(5)时, 选择矢量亥姆赫兹方程作为支配方程, 其形式为

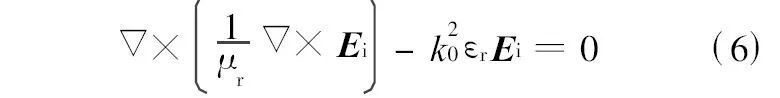
式中:εr 、μr 分别为复相对介电常数和复相对磁导率(考虑了介质的损耗);k0 为真空中的传播常数.根据变分原理可得到支配方程式(6)对应的泛函为

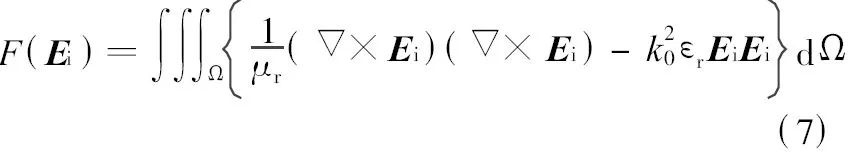
求解式(7)即可得到机壳表面的电场分布. 考虑到理想导体的趋肤效应, 对表面电场沿电场方向积分, 得到的就是信号线与机壳结合点处的表面干扰电压,这个电压即为内部高速电路的EMS 仿真分析的激励源.

1. 2 　建立内部高速电路模型通常, 电子设备的内部电路由分立器件、集成电路和高速传输线组成.对于电阻、电容、电感和晶体管一级的分立器件, 可采用建立在电路基本元器件(如晶管、电阻、电容等)工作机理和物理细节之上的SPICE 模型进行电路仿真.

对于集成电路, 应采用IBIS 模型对其进行仿真. IBIS 模型是通过一簇电流/电压和电压/时间曲线来描述各个器件管脚的输入输出特性的. 因为IBIS模型用一种标准的文件格式记录了如驱动源输出阻抗、上升/下降时间及输入负载等参数, 因此适合于电子设备内部高速集成电路的振荡和串扰等高频效应的计算与仿真.

对于内部PCB 板上的连接线来说, 当工作在低频时, 只须建立其集总模型, 将传输线用集总参数的电路等效即可, 而当传输线工作在较高频率时, 由于会产生较明显的传输线效应, 故必须为其建立分布模型, 即在准TEM 模式假设时, 将传输线划分为若干单元段, 每段用特征参数R 、L 、G、C 组成的网络等效, 建立其电报方程, 用Hspice 软件进行仿真, 当时钟频率继续上升到达GHz 时, 就必须建立其全波模型, 利用A nsof t HFSS 软件对其进行三维空间等效分析.

2 　仿真实例为了说明上述方法, 本文所使用的仿真模型由3 部分组成:①金属屏蔽机壳;②连接内部PCB 板的信号线或电源线;③放置在金属机壳内部的双层PCB 板和4 片集成电路插件. 其结构如图1 所示.仿真步骤如下:

(1)计算当入射电场幅值E0 =1 V /m 时的干扰电压. 采用Ansof t HFSS 软件仿真时的HFSS 模型如图2 所示, 其中金属屏蔽机壳外形尺寸为L ×W ×H =14 cm ×10 cm ×6 cm , 圆柱体的外接信号线直径为2 mm , 长度为40 cm , 材质为铜, PCB 板为双面板, 上层为铜质带状连接线和集成电路插件, 下层为铜质接地层, 中间是介电常数为2. 2 的绝缘介质Rogers RT /duroid 5880. 圆柱体的外接信号线通过屏蔽机壳上的一个直径为0. 2 mm 的圆孔与PCB板上的第一段带状连接线L1 相连(参考图1), 接地层的外形尺寸为L ×W ×H =12 cm ×8 cm ×0. 01cm , 通过一条短的细线与机壳相连. PCB 板上的4段带状连接线都为铜线, 其横截面相同, 为W ×H=0. 5 mm ×0. 06 mm , 长度分别为L1 =1 cm , L2 =1. 37 cm , L3 =2 cm , L4 =2. 75 cm(参考图1). 

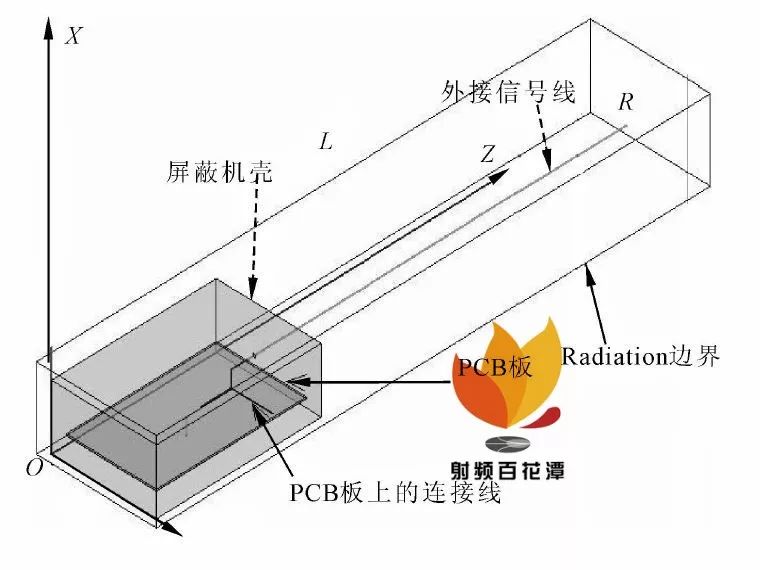
图2HFSS 模型

当频率为200 MHz 时, 外部干扰在信号线与PCB 连接点处的积分路径上的电场分布如图3 所示, 由此得到的连接点处不同频率时的干扰电压如图4 所示.由于假设屏蔽机壳为理想导体, 因此, 建模时将其设为“perfect E”边界条件, 按照软件要求在模型外面加了一个外形尺寸为L ×W ×H =46 cm ×12 cm ×7 cm 的长方体, 作为“Radiatio n”边界条件.

(2)建立内部高速电路的仿真模型. 建模时首先将图1 所示的内部PCB 板上的互连网络等效为由电阻R 和电容C 组成的电气等效电路, 如图5 所示. 利用A nsof t HFSS 软件建立带状连接线的全波模型, 输出其Hspice 等效电路仿真文件.

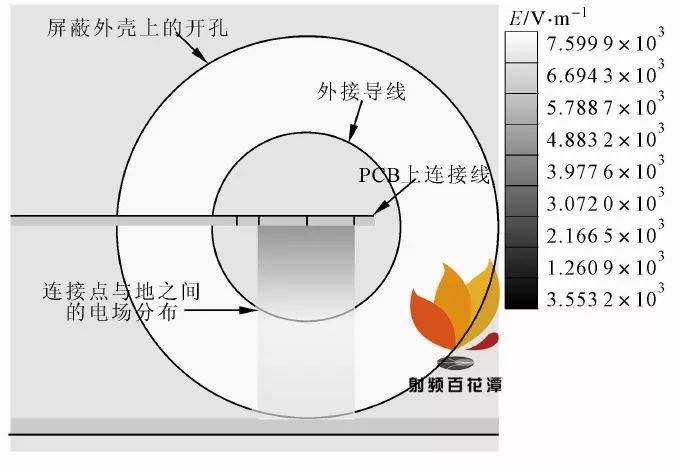
图3 　200 M Hz 时连接点处的电场分布

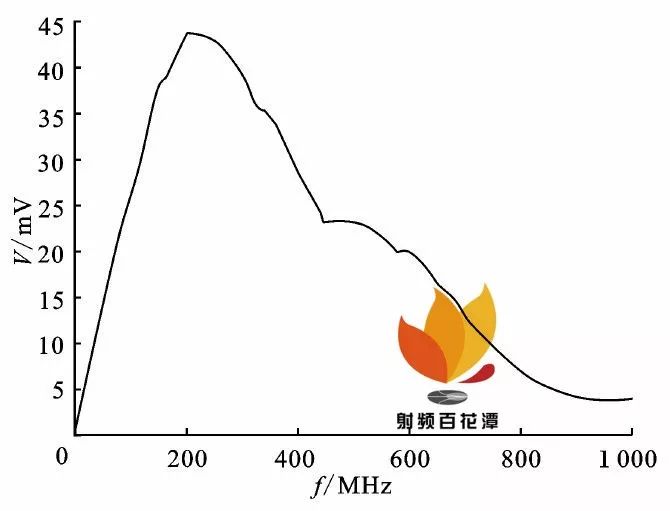
图4 　连接点处的干扰电压

再利用Hspice 建立整个内部高速电路的仿真模型.

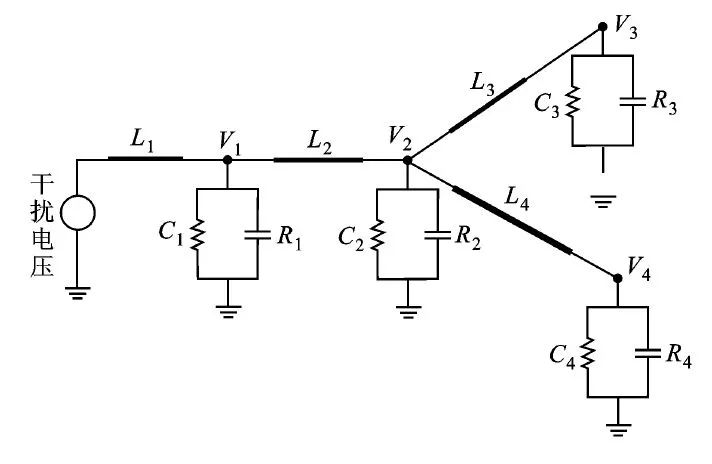
图5 　内部PCB 板的电气等效电路

(3)将第(1)步得到的干扰电压, 作为第(2)步得到的模型的输入, 由H spice 软件仿真分析感应到各个芯片输入端的干扰电压. 仿真结果如图6 所示. 由图6 可知, 当幅值为1 V /m 的平面电磁波干扰照射到图1 所示的具有屏蔽机壳的电子设备上时, 由信号线引入并感应到电路各处的干扰电压频率主要集中于25 MHz 左右, 感应到芯片IC1 和IC2 处的干扰电压幅值高于芯片IC3 和IC4 处的干扰电压幅值, 且幅值较大.

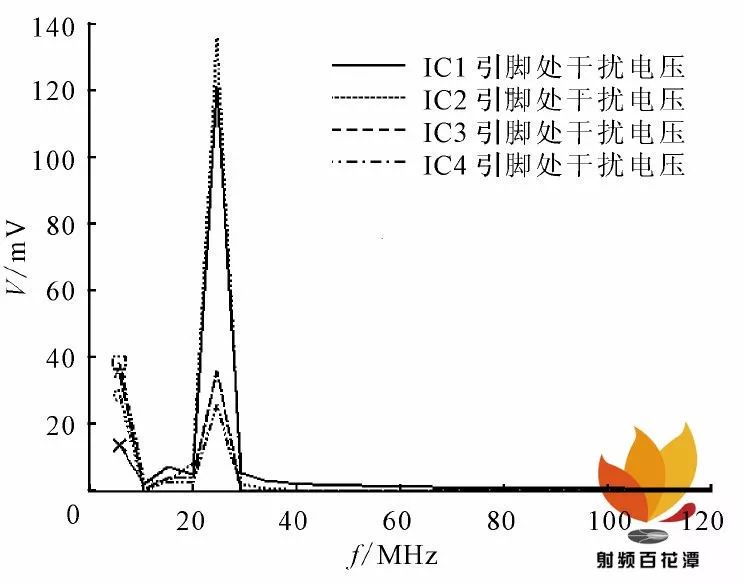
图6　内部电路各处的干扰电压

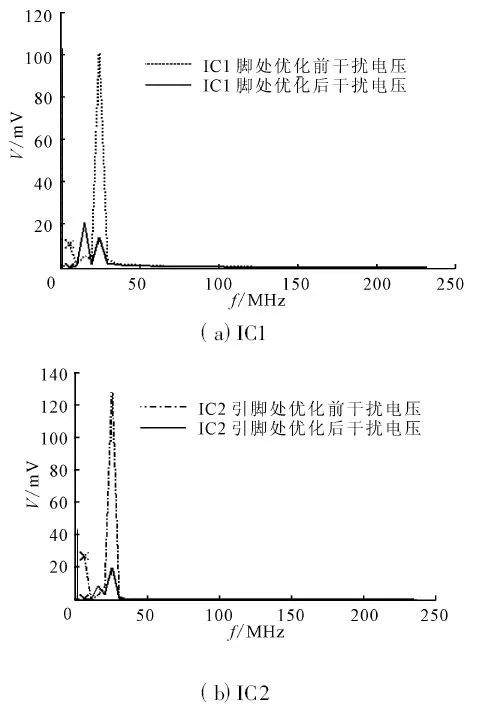
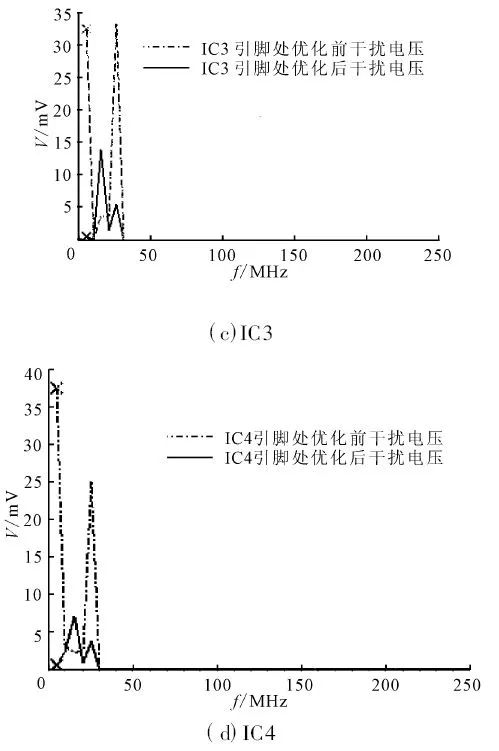
(4)为了使内部电路各处的干扰电压尽量小, 对图5 所示的网络结构进行了优化设计. 优化前各段连接线长度分别为L1 =1 cm , L2 =1. 37 cm , L3 =2cm , L4 =2.75 cm , 优化设计在各连接线原来长度的±20 %范围内进行. 优化设计结果为:当各连接线长度分别为L1 =1. 2 cm , L2 =1. 37 cm , L3 =1. 8 cm ,L4 =2. 75 cm 时, 感应到各处的干扰电压信号最小,如图7 所示. 由图可知, 优化设计后的内部电路各处感应的干扰电压确实比优化前减小了很多, 最为明显的是在IC2 处, 干扰电压从原来的138 mV 减小到优化后的20 mV. 由此可以得出结论:PCB 板上的连接线长度的匹配对提高系统的抗干扰能力起着至关重要的作用.

3 　结　论本文提出了一种分析具有屏蔽机壳的电子设备系统级EMS 的场路结合的新方法, 其特点是:对采用有限元法计算的屏蔽机壳表面电场直接积分, 得到信号线与机壳结合点处的表面干扰电压;将外部干扰对内部高速电路的影响等效为电压源的作用.本文提出的方法简单、直观, 避免了以往在EMS 分析时只以实验为主、缺乏理论依据的缺陷, 适用于大多数工作在电磁波干扰环境中的电子设备系统级的EMS 仿真分析. 另外, 利用本文所述方法建立的高速电路仿真模型, 不仅可以详细分析电子设备内部高速电路中干扰的传播情况, 对诸如串扰、延迟等信号完整性进行仿真, 而且可以对内部高速电路进行优化设计, 以提高系统的抗干扰性.(参考文献略）