训练模型：讨论两种训练方法

训练模型

一、讨论两种训练方法二、线性回归三、如何训练四、正规方程五、示例六、模型图像七、梯度下降八、梯度下降的陷阱

一、讨论两种训练方法

1、直接使用封闭方程进行求根运算，得到模型在当前训练集上的最优参数（即在训练集上使损失函数达到最小值的模型参数）2、使用迭代优化方法：梯度下降（GD），在训练集上，它可以逐渐调整模型参数以获得最小的损失函数，最终，参数会收敛到和第一种方法相同的的值。同时，我们也会介绍一些梯度下降的变体形式：批量梯度下降（Batch GD）、小批量梯度下降（Mini-batch GD）、随机梯度下降（Stochastic GD）。对于多项式回归，它可以拟合非线性数据集，由于它比线性模型拥有更多的参数，于是它更容易出现模型的过拟合。因此，我们将介绍如何通过学习曲线去判断模型是否出现了过拟合，并介绍几种正则化方法以减少模型出现过拟合的风险。

二、线性回归

线性回归预测模型

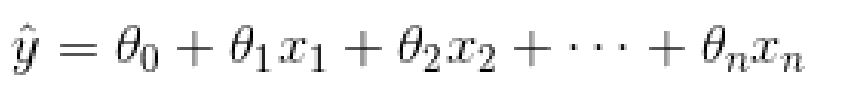
三、如何训练

训练一个模型指的是设置模型的参数使得这个模型在训练集的表现较好。为此，我们首先需要找到一个衡量模型好坏的评定方法。在回归模型上，最常见的评定标准是均方根误差。因此，为了训练一个线性回归模型，需要找到一个θ值，它使得均方根误差（标准误差）达到最小值。实践过程中，最小化均方误差比最小化均方根误差更加的简单，这两个过程会得到相同的θ因为函数在最小值时候的自变量，同样能使函数的方根运算得到最小值。线性回归模型的 MSE 损失函数：

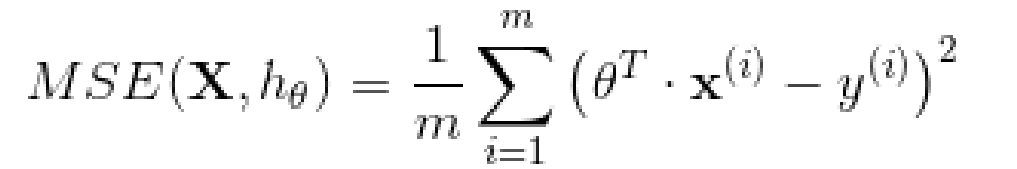
四、正规方程

为了找到最小化损失函数的 值，可以采用公式解，换句话说，就是可以通过解正规方程直接得到最后的结果。正规方程如下：

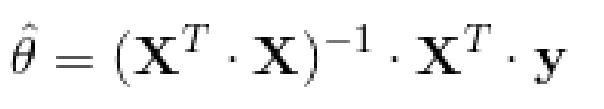
五、示例

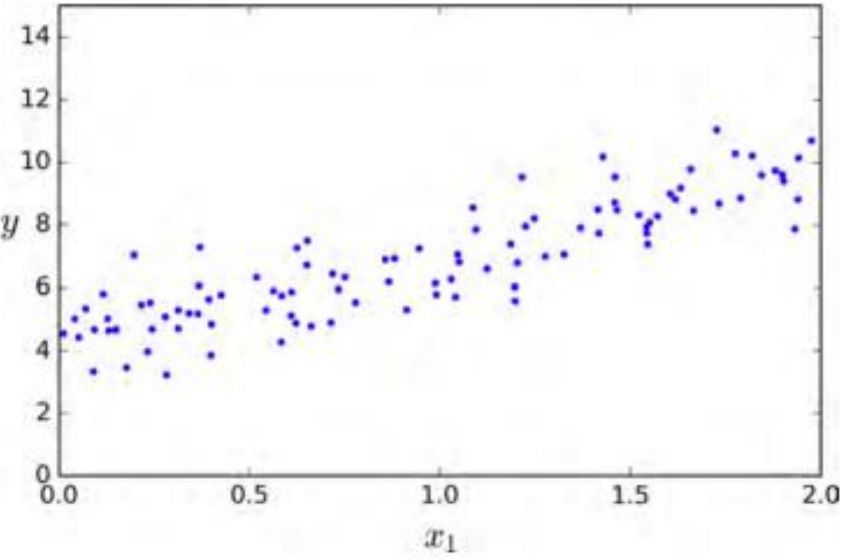
生成一些近似线性的数据来测试一下这个方程。

import numpy as npX = 2 * np.random.rand(100, 1)y = 4 + 3 * X + np.random.randn(100, 1)

X_b = np.c_[np.ones((100, 1)), X]theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

实际上产生数据的两个系数是4和3 。让我们看一下最后的计算结果。

>>> theta_bestarray([[4.21509616],[2.77011339]])

由于存在噪声，参数不可能达到到原始函数的值。现在我们能够使用 来进行预测：

X_new = np.array([[0],[2]])X_new_b = np.c_[np.ones((2, 1)), X_new]y_predict = X_new_b.dot(theta_best)y_predict>>>array([[4.21509616],[9.75532293]])

六、模型图像

plt.plot(X_new,y_predict,"r-")plt.plot(X,y,"b.")plt.axis([0,2,0,15])plt.show()

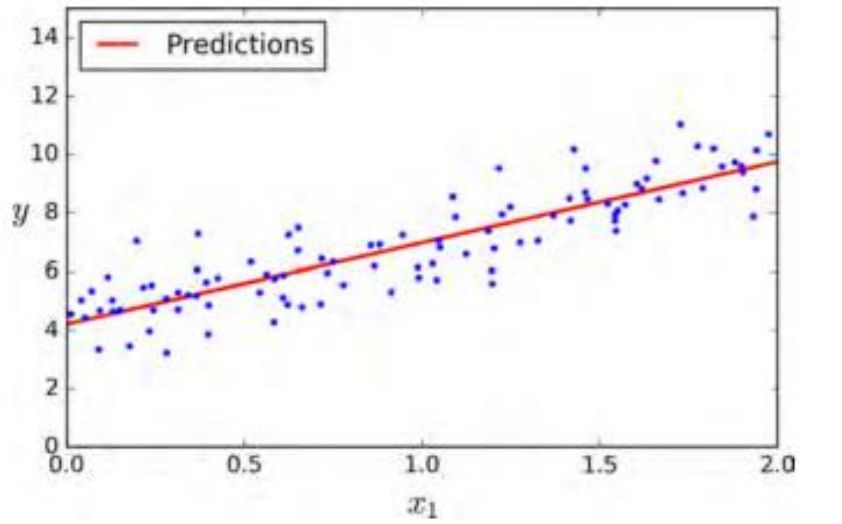
使用下面的 Scikit-Learn 代码可以达到相同的效果：

from sklearn.linear_model import LinearRegressionlin_reg = LinearRegression()lin_reg.fit(X,y)lin_reg.intercept_, lin_reg.coef_(array([4.21509616]),array([2.77011339]))lin_reg.predict(X_new)array([[4.21509616],[9.75532293]])

七、梯度下降

梯度下降是一种非常通用的优化算法，它能够很好地解决一系列问题。梯度下降的整体思路是通过的迭代来逐渐调整参数使得损失函数达到最小值。假设浓雾下，你迷失在了大山中，你只能感受到自己脚下的坡度。为了最快到达山底，一个最好的方法就是沿着坡度最陡的地方下山。这其实就是梯度下降所做的：它计算误差函数关于参数向量 的局部梯度，同时它沿着梯度下降的方向进行下一次迭代。当梯度值为零的时候，就达到了误差函数最小值 。具体来说，开始时，需要选定一个随机的 （这个值称为随机初始值），然后逐渐去改进它，每一次变化一小步，每一步都试着降低损失函数（例如：均方差损失函数），直到算法收敛到一个最小值。在梯度下降中一个重要的参数是步长，超参数学习率的值决定了步长的大小。如果学习率太小，必须经过多次迭代，算法才能收敛，这是非常耗时的。另一方面，如果学习率太大，你将跳过最低点，到达山谷的另一面，可能下一次的值比上一次还要大。这可能使的算法是发散的，函数值变得越来越大，永远不可能找到一个好的答案。最后，并不是所有的损失函数看起来都像一个规则的碗。它们可能是洞，山脊，高原和各种不规则的地形，使它们收敛到最小值非常的困难。梯度下降的两个主要挑战：如果随机初始值选在了图像的左侧，则它将收敛到局部最小值，这个值要比全局最小值要大。 如果它从右侧开始，那么跨越高原将需要很长时间，如果你早早地结束训练，你将永远到不了全局最小值。

八、梯度下降的陷阱

幸运的是线性回归模型的均方差损失函数是一个凸函数，这意味着如果你选择曲线上的任意两点，它们的连线段不会与曲线发生交叉（译者注：该线段不会与曲线有第三个交点）。这意味着这个损失函数没有局部最小值，仅仅只有一个全局最小值。同时它也是一个斜率不能突变的连续函数。这两个因素导致了一个好的结果：       梯度下降可以无限接近全局最小值。（只要你训练时间足够长，同时学习率不是太大 ）。