运算放大器驱动容性负载要考虑的稳定因素

问：ADI已经发布了大量有关处理电容负载和书籍中其他稳定性问题的信息，例如放大器研讨会系列，早期的Analog Dialogue期刊以及一些设计工具。但是，我现在需要复习。

A：好的。这就好了！

电容负载经常会产生问题，部分原因是它们会降低输出带宽和压摆率，但主要是因为运算放大器反馈环路中产生的相位滞后会导致不稳定。虽然一些电容负载是不可避免的，但放大器经常受到足够的电容负载以引起过冲，振铃甚至振荡。当必须驱动大容性负载（例如LCD面板或端接不良的同轴电缆）时，问题尤其严重 - 但精密低频和直流应用中也会出现令人不快的意外情况。

将会如此可以看出，运算放大器在配置为单位增益跟随器时最容易出现不稳定性，或者是因为（a）环路中没有衰减，或（b）大的共模摆动，尽管不会显着影响精度信号增益可以将环路增益调制到不稳定的区域。

运算放大器驱动容性负载的能力受到以下几个因素的影响：

1. 放大器的内部架构（例如，输出阻抗，增益和相位裕度，内部补偿电路）
2. 负载阻抗的性质
3. 反馈电路的衰减和相移，包括输出的影响负载，输入阻抗和杂散电容。

在上面引用的参数中，放大器输出阻抗，由输出电阻 R _O 表示，是影响容性负载性能的最重要因素之一。理想情况下， R _O = 0的其他稳定运算放大器将驱动任何容性负载而不会出现相位下降。

为了避免因轻负载而牺牲性能，大多数放大器在内部都没有经过大量的容性负载补偿，因此必须使用外部补偿技术来优化那些必须处理运算放大器输出端的大容性负载的应用。典型应用包括采样保持放大器，峰值检波器和驱动未端接同轴电缆。

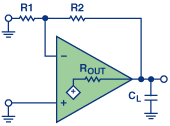
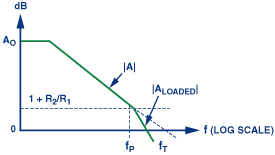
如图1和图2所示，电容负载会影响开环增益同样，无论有源输入是在同相还是在反相端：负载电容 C _L ，与开环输出形成一个极点阻力， R _O 。加载的增益可表示如下：

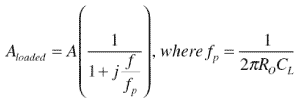
和 A 是放大器的空载开环增益。

-20由极点贡献的dB /十倍斜率和90°滞后，加到-20 dB斜率和放大器贡献的90°（加上任何其他现有滞后），导致闭合率（ROC）增加到一个值每十年至少40 dB，这反过来会导致不稳定。

本说明讨论了容性负载对某些放大器电路性能影响的典型问题，并提出了解决不稳定性问题的技巧他们提高了。

问：那么，不同的电路需要不同的技术？

A：是的，绝对！您将选择最适合您设计的补偿技术。下面详细说明了一些例子。例如，这是一种补偿技术，它具有通过RC反馈电路滤除运算放大器噪声的额外好处。

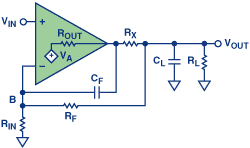
图3显示了一种常用的补偿技术，通常被称为 in - 循环补偿。一个小串联电阻 R _x 用于将放大器输出与 C _L 分离;插入反馈环路的一个小电容 C _f ，在 C _L 周围提供高频旁路。

为了更好地理解这种技术，请考虑图4所示电路的重绘反馈部分.VB连接到放大器的负输入。

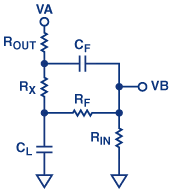
想一想电容， C _f 和 C _L ，作为直流开路和高频短路。考虑到这一点，并参考图4中的电路，让我们一次将这个原理应用于一个电容器。

案例1（图5a）：

C _f 短路时， R _x << R _f ， R _o << R _in ，极点和零点是函数 C _L ， R _o ， R _x

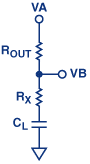
因此，

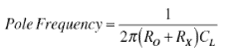
和

案例2.（图5b）：

当 C _L 打开时，极点和零点是 C _f 的函数。

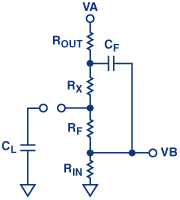
因此，

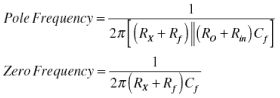
通过将情况1中的极点等于情况2中的零，并将情况2中的极点等于情况1中的零，我们推导出以下两个方程式：

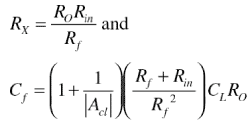
C _f 的公式包括术语 A _cl （放大器关闭 - 循环增益，1 + R _f / R _in ）。通过实验，发现1 / A _cl 项需要包含在 C _f 的公式中>。对于上述电路，仅使用这两个方程就可以补偿任何带有任何电容负载的运算放大器。

虽然这种方法有助于防止在使用大容性负载时振荡，但它会降低闭环电路带宽急剧下降。带宽不再由运算放大器确定，而是由外部组件确定， C _f 和 R _f ，产生闭环带宽： f _{-3 dB} = 1 /（2π C _f R _f ）。

这种补偿技术的一个很好的实际例子可以用AD8510看到，这款放大器可以安全地驱动高达200 pF，同时仍能保持45°相位单位增益交叉的余量。 AD8510采用图3电路，增益为10，输出端负载电容为1 nF，典型输出阻抗为15欧姆， R _{x 和 C f 为2欧姆和2 pF。图6和图7的方波响应显示了无补偿振铃的快速响应，以及较慢但单调的校正响应。}

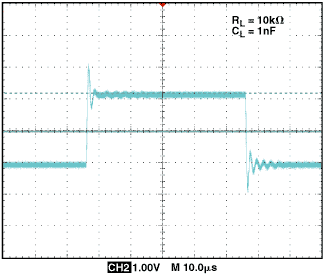
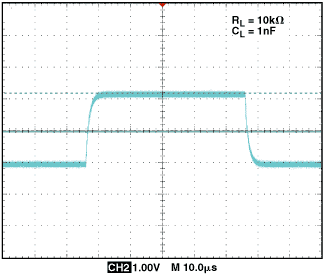
在图7中，请注意，因为< em> R _x 位于反馈回路内部，其存在不会降低直流精度。但是， R _x 应始终保持适当的小，以避免输出摆幅过大和转换速率降低。

注意：这里讨论的行为通常用于常用的电压反馈放大器。使用电流反馈的放大器需要不同的处理 - 超出了本讨论的范围。如果这些技术与电流反馈放大器一起使用， C _f 中固有的积分将导致不稳定。

环路外补偿

问：是否有更简单的补偿方案使用更少的组件？

A：是的，最简单的方法是使用与输出串联的单个外部电阻。这种方法有效但性能昂贵（图8）。

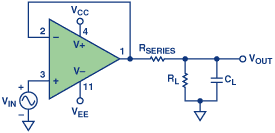
这里有一个电阻R _系列，位于输出和负载之间。该电阻的主要功能是将运算放大器输出和反馈网络与容性负载隔离。在功能上，它在反馈网络的传递函数中引入了零，这减少了在较高频率下的环路相移。为了确保良好的稳定性，R _系列的值应使得零增加至少比放大器电路的单位增益交叉带宽低十倍。所需的串联电阻量主要取决于所用放大器的输出阻抗;从5欧姆到50欧姆的值通常足以防止不稳定。图9显示了OP1177的输出响应，其负载为2 nF，正输入端为200 mV峰峰值信号。图10显示了相同条件下的输出响应，但信号路径中的电阻为50欧姆。

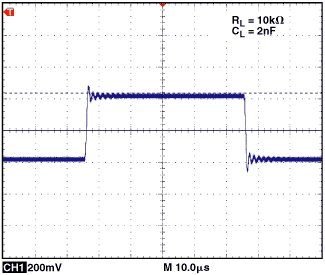
输出信号将通过系列的比率衰减抵抗总阻力。这将需要更宽的放大器输出摆幅以获得满量程负载电压。非线性或可变负载会影响输出信号的形状和幅度。

缓冲网络

问：如果我使用的是轨到轨放大器，你能建议一种能够保持输出摆幅并保持增益精度的稳定方法吗？

A：是的，RC系列电路从输出到接地，缓冲器方法适用于需要全输出摆幅的低压应用（图11）。

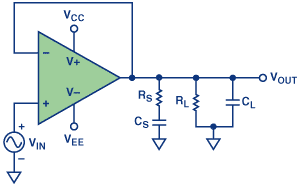
取决于容性负载，应用工程师通常采用经验方法来确定 R _s 和 C _s 的正确值。这里的原理是对发生峰值的附近的频率进行电阻性地降低放大器的输出 - 从而缓冲放大器的增益，然后使用串联电容来降低较低频率的负载。因此，程序是：检查放大器的频率响应以确定峰值频率;然后，通过实验应用电阻负载值（ R _s ）将峰值降低到令人满意的值;然后，计算 C _s 的值，使断点频率约为峰值频率的1/3。因此， C _s = 3 /（2π f _p R _s ），其中 f _p 是峰值出现的频率。

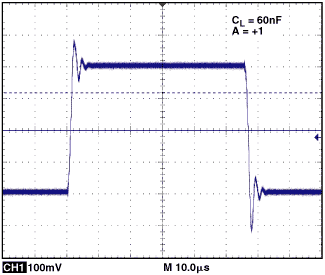
在观察示波器上的瞬态响应（带电容负载）时，也可以通过反复试验确定这些值。 R _s 和 C _s 的理想值将产生最小的过冲和下冲。图12显示了AD8698的输出响应，响应其正输入端的400 mV信号，具有68 nF负载。在没有任何外部补偿的情况下，此处的过冲小于25％。如图13所示，一个简单的缓冲网络可将过冲减少到10％以下。在这种情况下， R _s 和 C _s 分别为30欧姆和5 nF。

问：好的。我理解这些关于处理放大器输出上的电容负载的例子。现在，输入端的电容是否也值得关注？

A：是的，运算放大器输入端的容性负载会导致稳定问题。我们将通过几个例子来说明。

当运算放大器用作电流输出DAC的缓冲器/放大器时，一种非常常见且典型的应用是电流 - 电压转换。输入端的总电容包括DAC输出电容，运算放大器输入电容和杂散布线电容。

运算放大器输入端可能出现大电容的另一种常见应用是过滤器设计。一些工程师可能在输入端放置一个大电容（通常与电阻串联），以防止RF噪声通过放大器传播 - 忽略了这种方法可能导致严重振铃或甚至振荡的事实。

为了更好地理解代表性案例中的情况，我们分析图14的电路，展开其反馈电路的等效电路（输入， V _{in < / sub>，onrounded）导出反馈传递函数：}

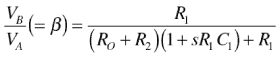
给出位于

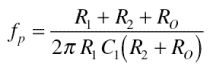
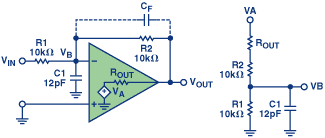
的极点此函数表示噪声增益（1 /β）曲线在高于中断频率 20 dB /十进制， f _p 。如果 f _p 远低于开环单位增益频率，则系统变得不稳定。这对应于约40dB /十倍的闭合速率。闭合速率定义为开环增益（dB）曲线（在大多数感兴趣的频率下为-20 dB /十倍）和1 /β的斜率之间的差异幅度，在频率附近它们交叉（环路增益= 0 dB）。

为了解决由 C ₁ 引起的不稳定性，一个电容器， C _f ，可与 R ₂ 并联，提供零点，可与极点匹配， f < sub> p ，降低闭合率，从而增加相位裕度。对于相位裕度为90°，选择 C _f =（ R ₁ / R ₂ ） C ₁ 。

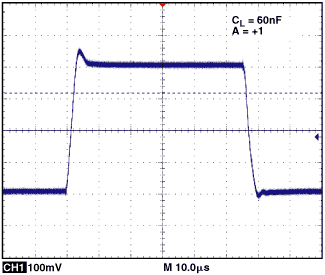
图15显示了AD8605在图14配置中的频率响应。

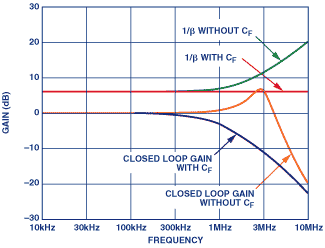
问：我可以预测相位余量是多少，或者我应该期待多少峰值？

答：是的，方法如下：

您可以使用以下公式确定未补偿峰值的数量：

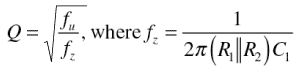
其中 f _u 是单位增益带宽， f _z 是1 /β曲线的断点， C ₁ 是总电容 - 内部和外部 - 包括任何寄生电容。

相位裕度（Φ _m ）可通过以下公式确定：

AD8605的总输入电容约为7 pF。假设寄生电容约为5 pF，则闭环增益将具有5.5 dB的严重峰值，使用上述等式。以相同的方式，相位裕度约为29°，运算放大器的自然相位响应为64°，严重降低。

问：如何确保运算放大器如果我想在输入端直接使用RC滤波器，电路是否稳定？

A：您可以使用与上述相似的技术。这是一个例子：

通常希望从放大器的有源输入端子接地电容，以减少高频干扰，RFI和EMI。该滤波电容对运算放大器动态的影响与增加的杂散电容相似。由于并非所有运算放大器都以相同的方式运行，因此有些运算放大器的输出电容会比其他运放放大。因此，在任何情况下，引入反馈电容 C _f 作为补偿是有用的。为了进一步降低RFI，放大器端子上的一个小串联电阻将与放大器的输入电容相结合，以便在无线电频率下进行滤波。图16显示了一种方法（左图），与显着改进的电路（右图）相比，该方法难以保持稳定性。图17显示了它们叠加的方波响应。

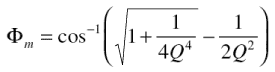
问：您之前提到将杂散电容添加到总输入电容中。杂散电容有多重要？

A：不合理的杂散电容会对运算放大器的稳定性产生不利影响。预测并最小化它是非常重要的。

电路板布局可能是杂散输入电容的主要来源。该电容发生在运算放大器求和点的输入走线上。例如，一平方厘米的PC板，其周围有一个接地层，将产生约2.8 pF的电容（取决于电路板的厚度）。

要减小这个电容：始终保持输入走线尽可能短。将反馈电阻和输入源尽可能靠近运算放大器输入。保持接地平面远离运算放大器，尤其是输入端，除非电路需要，并且同相引脚接地。当真正需要接地时，使用宽走线以确保接地的低阻抗路径。

问：可以将单位增益稳定的运算放大器用于单位 - 获得？ OP37是一款出色的放大器，但必须以至少5的增益使用才能保持稳定。

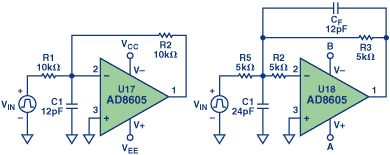
A：您可以通过欺骗它们来使用此类运算放大器获得较低的增益。图18显示了一种有用的方法。

在图18中， R _B 和 R _A 在高频下提供足够的闭环增益以稳定放大器， C ₁ 使其在低频和直流时恢复为单位。根据放大器的最小稳定增益，计算 R _B 和 R _A 的值非常简单。对于OP37，放大器需要至少为5的闭环增益才能保持稳定，因此 R _B = 4 R _A ，β= 1/5。对于高频，其中 C ₁ 的行为类似于直接连接，运算放大器认为它的闭环增益为5，因此是稳定的。在直流和低频时， C ₁ 的行为类似于开路，负反馈没有衰减，电路的行为类似于单位增益跟随器。

下一步是计算电容值 C ₁ 。应选择 C ₁ 的良好值，使其提供至少比电路转角频率低十十倍的中断频率（ f < sub> -3 dB ）。

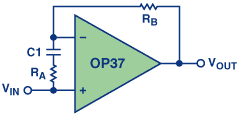
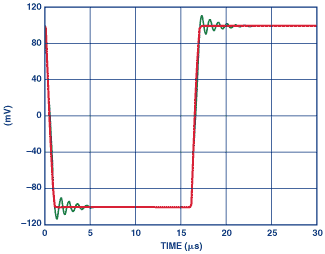
图19显示了响应2 V pp输入步骤的OP37输出。使用上面的等式选择补偿分量的值， f _c = 16 MHz

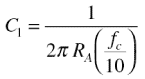
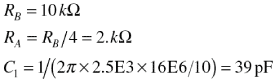
问：这种方法是否也可用于反相配置？我仍然可以使用相同的方程式吗？

A：对于反相配置，分析类似，但是闭环方程式收益略有不同。请记住，运算放大器反相端的输入电阻现在与高频 R _A 并联。该并联组合用于计算 R _A 的值，以获得最小稳定增益。电容值 C ₁ 的计算方法与同相情况相同。

问：使用这种技术有缺点吗？

答：确实有。增加噪声增益会增加较高频率的输出噪声电平，这在某些应用中可能是不可容忍的。在从动配置中应小心使用布线，尤其是高源阻抗。原因是在增益大于1的频率上通过电容向放大器的同相输入提供正反馈会引起不稳定性，并增加噪声。