

使用单个加速度计设计准确度高的计步器
描述
应用说明AN-602检查了使用ADI公司的加速度计制作简单但相对准确的计步器。从那时起,引入了更新的设备,允许在更加成本敏感的应用中使用加速度计。因此,诸如计步器之类的应用在诸如蜂窝手机之类的许多消费设备中发现。
鉴于这种趋势,使用单个加速度计对计步器进行了更仔细的检查。实施AN-602技术是为了复制其结果。尽管该算法表现良好,但相同的准确度并未重复。特别是,人与人之间的变化比预期的更大,以及当一个人使用不同的步速和步幅时。这导致了对算法潜在改进的调查。
使用带有ARM7内核的ADuC7020精密模拟微控制器和两个不同的计步器测试板进行测试:一个带有2轴ADXL323加速度计,另一个带有3轴ADXL330加速度计。首先使用ADuC7020和ADXL323评估板,增加了16×2 LCD显示屏。第二个使用定制板。
AN-602方法
AN-602中使用的技术基于以下原则:一步中的垂直“反弹”直接与步长,如图1所示。
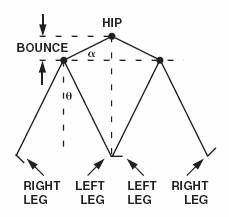
角度α和θ相等,因此步幅可以显示为最大垂直位移的倍数。给定相同的角度,对于较高或较矮的人来说,垂直位移会更大或更小,从而解决了腿长的差异。
不幸的是,加速度计测量的是加速度而不是位移的变化。必须先将加速度转换为距离才能使用。在AN-602设置中,有限的计算能力要求使用简单的公式来近似将加速度转换为距离所需的双积分。
ADuC7020具有充足的处理能力,本实验尝试直接计算离散积分。选择一种简单的方法来做到这一点。在确定每个步骤之后,添加该步骤中的所有加速度样本以获得一组速度样本。将每个步骤的速度样品归一化,使得最终样品为零。然后将它们加在一起以获得位移值。
最初,这项技术看起来很有希望,因为测量距离对于一个多次走路的受试者来说是相对一致的。不幸的是,人与人之间的差异加剧了,一个主题在不同节奏下的差异也在加剧。这导致调查问题是否与模型本身有关。
理解模型
这个模型有两个主要假设:脚实际上是单个点(或者球),每只脚在地面上的冲击是完全有弹性的。然而,这些假设都不是这样。基于这些实验,可以肯定地说,这些假设和现实之间的差异解释了大部分遇到的变化。
要理解这一点,有助于查看几个步骤的测量加速度,如图所示在图2中显示了一个步骤中“弹簧”的不同来源。
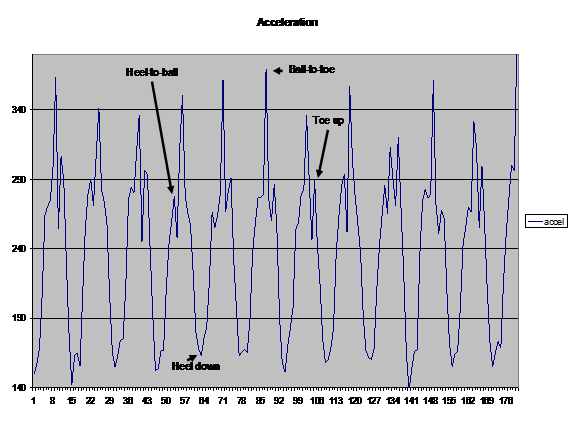
图2显示了尝试将测量的加速度精确转换为距离时遇到的问题。使用峰峰值变化的方法 - 甚至那些整合数据的方法 - 都会遇到这样的数据问题。造成这种困难的原因是不同人的步骤在春季从一种测量到另一种测量的变化,或者是一个人使用不同步幅的步骤。
图3显示了相同的主体,步伐越来越快。峰峰值加速度差异较大,各种弹簧点看起来不同。 “弹簧”数据与“实际”数据的数量与图2中的不同。但算法仅看到一组加速度测量,并且不知道这些测量的上下文。因此,问题是在不删除有用数据的情况下消除弹簧在主体步骤中的影响。
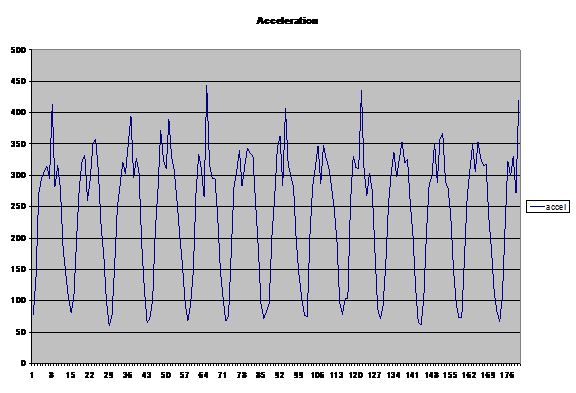
两个图之间存在重要差异:在图3中,底部是每个步骤的曲线略窄于图2的曲线,并且曲线的顶部更一致,具有更少的独特峰值。与最小和最大样本值相比,这些差异导致更高的平均值。
为了进行比较,图4显示了不同个体的数据图。步幅长度与图2中的主题非常相似。然而,数据本身看起来非常不同。
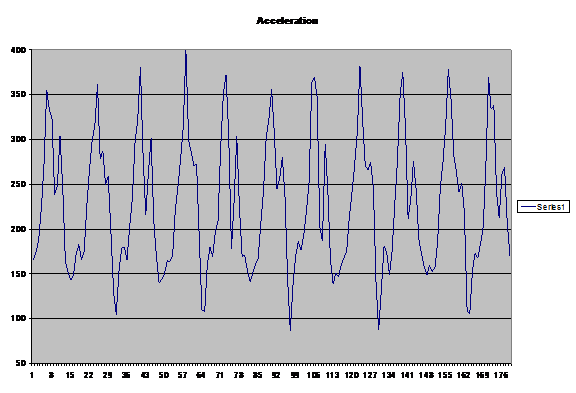
这个主题的步幅比图2所示的更多,但是这两组数据代表了大致相同的距离。因此,仅根据峰值计算距离将产生广泛变化的结果。使用简单的双重集成会遇到同样的问题。
解决弹簧问题
所有使用直接计算得出解决这个问题的方法都有同样的问题,导致一系列失败的尝试以消除弹簧的方式规范化数据。主要原因似乎是他们需要一些关于数据上下文的知识,但在实际使用中,系统不知道外面发生了什么。它只有数据点。我们的解决方案需要能够在没有上下文的情况下对数据进行操作。
在一段令人沮丧的情况下,这个问题的可能解决方案就出现了。如前所述,数据在从较慢到较快的速度变化时会发生变化,但由于弹簧发生的变化较小,步幅更长,速度更快。结果是相对于数据最小值和最大值的平均值更高。但是这会阻碍新的数据吗?
在视觉上,由于图4所示的步骤反弹量,很难确定这一点。但是计算表明平均值与峰值之间的关系因此,确定步行距离的简单算法的候选者是:
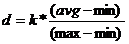
这个计算是针对每个步骤完成的,由不同的步骤决定 - 寻找算法。步进算法使用8点移动平均值来平滑数据。它搜索最大峰值,然后搜索最小值。当移动平均值越过零点时计算步长,该零点是该步骤的总体平均值。距离算法中使用的数据考虑了移动平均值的4点延迟。
这个简单的解决方案在第一个主题上适用于各种步幅。对于其他科目,它也做得相当好。但是一些受试者产生的距离与该组的平均测量距离相差10%。这不在±7.5%误差范围内,该误差范围是未校准测量的目标。需要另一种解决方案。
尽管如此,上一次测试中使用的比率似乎反映了不同受试者步骤的弹簧差异。尝试结合我们在这里研究的两种方法是有意义的。回到使用双积分的最初想法,使用该比率作为校正因子进行计算以去除弹簧数据。得到的公式是:
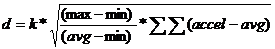
其中:
d是计算的距离
k是常数乘数
max是在此步骤中测量的最大加速度
min是在此步骤中测量的最小加速度avg是步长的平均加速度值
accel表示步骤的所有测量加速度值
此算法适用于各种主题和步调,变化约+ 6%/ -4%。该算法通过调整乘数k,可以轻松校准特定个体和速度。该代码还可以在步幅长度上执行平均值以平滑逐步变化。这里提到的结果不包括使用这种平均值。
在这个实验中,只使用了X轴和Y轴。如果需要所有三个轴,则选择3轴加速度计以获得灵活性。发现两个轴足以完成任务,因此可以使用ADXL323代替ADXL330。由于引脚配置与Z轴输出相同,所以可以使用相同的布局。
该实验专注于为计步器的距离测量获得良好的结果。步数计算算法的评估仅足以确保它在行走或跑步时运作良好。在数百个步行或跑步步骤中,测量的步数落在实际数量的一个或两个步骤内。然而不幸的是,这种简单的算法可能会受到非步行运动的欺骗。 AN-602中描述的时间窗口功能可用于通过忽略在预期时间窗口之外发生的错误步骤来最小化错误计数,同时保留在用户改变速度时适应的能力。
-
使用单个加速度计提高计步器的性能2023-01-31 1822
-
加速度计的安装方法分享2022-04-16 7143
-
2460-010加速度计2021-05-28 1211
-
MEMS加速度计的概念,MEMS加速度计的原理2020-06-01 5028
-
Mems加速度计对于温度测量是准确2020-03-06 2447
-
基于加速度计的倾角测量精度提高2019-07-18 2729
-
认识加速度计的关键指标2019-01-21 4914
-
加速度计的技术规格详解2018-10-18 3262
-
一文带你了解加速度计2018-07-07 15297
-
通过单个加速度计增强计步器的性能2012-12-13 904
全部0条评论

快来发表一下你的评论吧 !

