

一种基于神经网络的多维频谱推理方法
电子说
描述
1 引言
在现代化战场条件下,作战平台或用频系统并不一定全部装备有专业的频谱监测设备,更多的是来源于作战平台或用频系统自身的频谱感知能力,因此,这些频谱监测数据在时域、空域、频域等多个维度上都是非常稀疏的甚至是非常匮乏的。需要对有限的、不连续的时空频多维分布式频谱监测进行数据汇集、融合,并对这些数据做频谱推理预测,形成战场复杂电磁环境的态势信息,并形成可用频谱资源的预测分析,从而为战场频谱管控提供依据。
频谱推理技术是认知通信的重要基础,其能够通过模式挖掘、机器学习等方法为装备系统提供在未知区域、未来时间或陌生频谱的信道占用情况,在很大程度上提高了复杂电磁环境下的装备生存适应能力,其在现代化战争中的意义不容忽视。
频谱推理是基于历史已知频谱数据来挖掘数据内在的相关性或者规律性,以获得将来未知无线频谱的数据状态[1]。频谱推理也是一把双刃剑,一方面它能够通过历史数据来预测信道未来某一段时间内的信道状态,提供非授权用户的吞吐量,能够缩短感知时间在自适应频谱感知中的能量消耗;另一方面,它也会不可避免地带来预测虚警和预测漏检[2-3]。
现有的频谱推理技术主要关注于一维的时间维度,而频率和空间维度上的推理技术则极少涉及,G?Ding等[4]验证了频谱状态的可预测性。对于时间维度频谱推理,隐马尔可夫模型(Hidden Markov Model,HMM)推理法和神经网络(Neural Network,NN)方法具有较好的推理精度,然而关于这两种方法的研究大多局限于下一时隙的占用情况推理,这与现实应用场景还有很大的差距。此外,隐马尔科夫模型推理法[5]的推理准确度受限于所用转换矩阵的阶数,越复杂的场景,模型所需的阶数越高,其中隐含的状态规律越难以描述,而且模型运算的复杂度会呈指数关系上升,因而,HMM模型并不适用于复杂的频谱推理场景。相对而言,NN算法[6]能够通过神经元的作用模拟应用场景中存在的非线性转化关系,并通过离线学习得到网络中节点间的权重值,对于更复杂的电磁频谱环境,可以增加神经网络的隐藏层数量[7]和各层的神经元数量[8]等。因而,NN算法相对于HMM算法更适用于多维度复杂电磁频谱推理场景。
鉴于频谱在空间和频率维度上的关联特性,NN算法可分别用于一维空间和一维频率维度频谱推理。本研究结合NN算法的优缺点,提出一种适用于时间维度多时隙频谱的推理算法——LSTM(Long Short Term Memory)算法,并以此为基础,分别设计可用于时频二维频谱推理以及时空频三维的频谱推理方法,后者可以完全移植到网格结构的应用场景中。目前,多维频谱推理技术尚处于初步探索研究阶段,还没有形成较为完善的理论体系,也缺少实际应用场景验证。
2 长短时记忆网络(LSTM)推理法
相关研究证明,信道状态具有高度的自相关特性,且伴随着不同的时移,相关性呈现逐渐下降的趋势。LSTM推理法在时间或者空间序列数据的处理上具备较大的优势[9]。LSTM网络单元结构如图1所示:
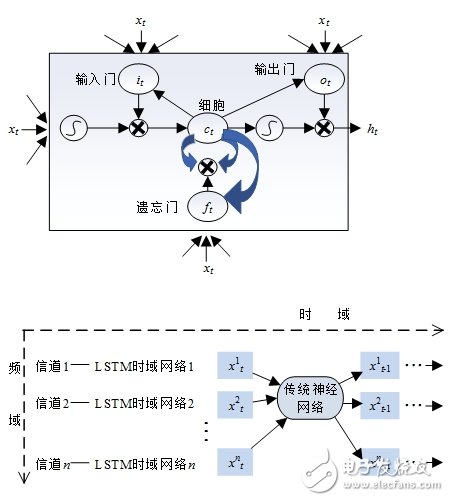
图1 LSTM网络单元结构
长短时记忆网络LSTM克服了RNN(Recurrent Neural Networks)网络训练过程中无法快速收敛的缺点[10],其通过引入三个门单元(输入门、遗忘门、输出门)来合理地控制历史与现在信息之间的关系,如图1所示,LSTM主要涉及的公式如下:
it=σ(Wxixt+Whiht-1+Wcict-1+bi) (1)
ft=σ(Wxfxt+Whfht-1+Wcfct-1+bf) (2)
ct=ft⊙ct-1+it⊙tanh(Wxcixt+Whcht-1+bc) (3)
ot=σ(Wxoxt+Whoht-1+Wcoct+bo) (4)
ht=ot⊙tanh(ct) (5)
其中,σ为逻辑S型函数,i、f、o、c为相应的输入门、遗忘门、输出门和记忆细胞激活向量,⊙表示向量间对应元素相乘,W(..)代表相应的各个权重矩阵,其中从细胞到各个门的矩阵为对角阵,而其余的各权重矩阵为非对角阵。
与一维时间序列频谱推理相匹配的LSTM网络结构如图2所示,基于LSTM网络的频谱推理方法可以灵活地调整推理网络结构,进而可以在推理不同时隙长度的应用中进行切换。与此同时,该方法的另外一个优势是,普通的推理算法(HMM或NN等)只能够对共享信道的可用性与否(即0-1值)进行推理判定,而LSTM方法还可以对信道的能量水平进行推理,从而极大地增加了认知设备在接入信道过程中设计接入判定准则时的灵活性,进一步提升了接入信道的效率,并降低了认知设备的感知能量消耗水平。
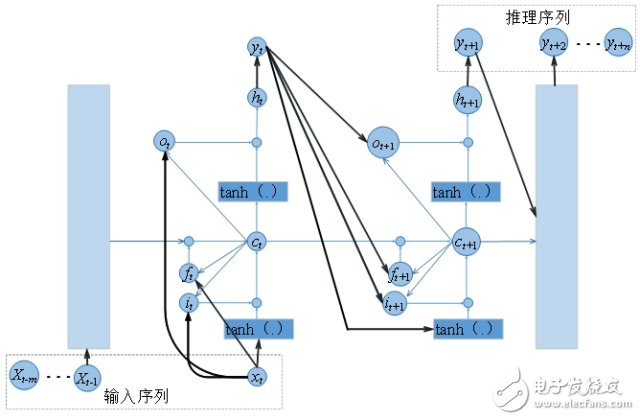
图2 一维时间序列推理LSTM网络结构示意图
3 时频二维频谱推理法(2D混合网络)
基于多种网络算法的结合算法能够通过不同网络的特长优势匹配而达到更为满意的处理或推理效果,因此,混合神经网络在频谱推理领域的应用前景巨大。多项研究分析表明,频谱的使用情况在频域上也存在很大的相关性,这里提出了一种LSTM网络与神经网络结合的适用于时频二维频谱推理的算法,算法中的网络关系如图3所示:
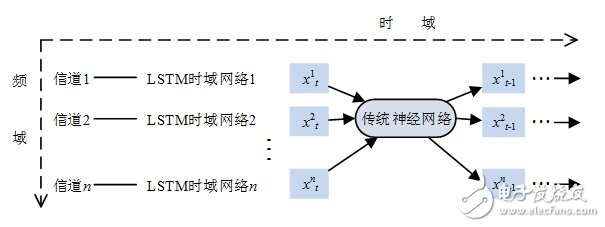
图3 时频二维频谱推理网络关系图
该混合网络主要基于时频域频谱所具有的相关性而构建。LSTM通过遗忘门表达出历史感知数据对未来推理数据的潜在影响关系。在无神经网络加入时,频谱推理的过程实现多条并行的时间序列推理功能,且相互之间无关联,而在神经网络与LSTM网络结合之后,混合网络既能用于推理其中一条或多条未知信道的占用情况,也可以推理整个信道所占频域的下一时隙(或多时隙)的使用情况。
用于时频域频谱推理的混合神经网络参数结构如图4所示,图4只描述了时隙t时的频谱推理过程,从图4可以看出,不同信道的LSTM结构是独立的平行关系,在此基础上,时隙t得出的各信道输出被当做输入值传输到MLP推理器中,经过该推理器处理后,得出下一时隙(t+1)或继续输入得到未来多个时隙的各信道占用情况。由于LSTM与神经网络相对明确的连接关系,在训练过程中,混合网络的后向传播过程基本等价于原来二者训练方式的加和,因而该混合网络并没有明显增加训练的复杂度,在一定的针对性训练操作之后,各前向权重矩阵和偏差值收敛到稳定值,继而可以用于后续的二维频谱推理过程。
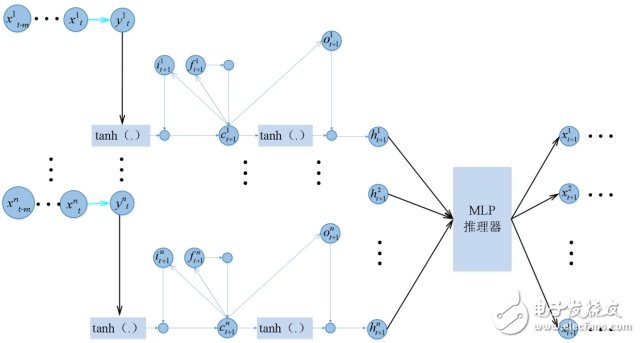
图4 时频二维频谱推理网络参数关系示意图
4 时空频三维频谱推理法(3D混合网络)
在LSTM算法和时频频谱推理算法的基础上,提出一种适用于网格结构的时空频频谱推理算法。在网格结构的频谱推理中,已知多个不同空间节点在时间和频率维度上的频谱感知信息,需运算推测出未知空间位置的频谱占用情况(或功率水平),提出能够满足该需求的推理算法网络结构如图5所示:
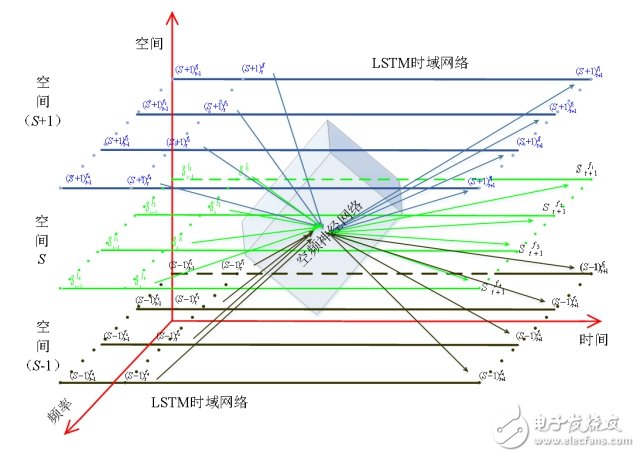
图5 时空频三维频谱推理网络示意图
在该网络结构中,时间维度使用LSTM基础网络,频率和空间维度使用神经网络。其中,未知节点位于空间S,而(S-1)与(S+1)等空间节点的频谱使用情况是已知信息,在网络的训练过程中,多个空间(不限于图中给出的三个)的历史信息作为输入信息,而输出可以根据实际需求进行调整,若仅需要空间S的未来频谱使用情况,则可以仅以作为输出。同时,各权重关系可以通过适当的删减来匹配实际中的影响关系,同时降低权重反向迭代过程中具备的运算压力。
在该3D神经网络中,传统神经网络结构可以进行适当的改进或者直接被替换成推理效果更好的卷积神经网络(CNN,Convolutional Neural Networks)等结构。可以看出,该3D神经网络结合了空间频谱的相对关系,能够通过调整网络中的连接关系以适用于时空频多维频谱数据。具体来说,该立体结构混合神经网络能够推理点(信道时隙点)、线(单信道或单一时隙或不同空间时隙点)、面(多信道时隙或多信道空间或多时隙空间)、体(信道时隙空间)结构的频谱占用情况。
5 频谱推理技术比较
已有频谱推理算法与当前提出的各频谱推理算法的参数与性能对比如表1所示:
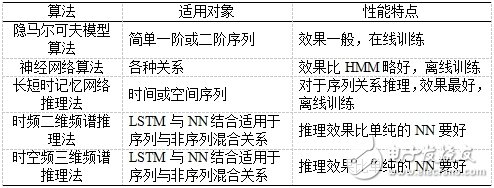
传统的隐马尔可夫模型算法不适用于复杂场景;神经网络算法可适用于复杂场景,但训练较慢;长短时记忆网络推理法适用于复杂场景下的序列关系,且训练较快;时频二维频谱推理法适用于二维关系场景,训练速度可通过与基因算法结合来改进;时空频三维频谱推理法适用于三维关系场景,训练速度可通过与基因算法结合来改进,网络结构也可进一步优化。
6 结束语
本文提出的适用于时间维度多时隙频谱的推理、时频二维频谱推理以及时空频三维的频谱推理方法能够在有限的、不连续的时空频多维频谱监测数据情况下实现频谱推理预测,从而为战场频谱管控提供支撑。该研究目前处于仿真试验阶段,其有效性尚待验证。
-
人工神经网络模型是一种什么模型2024-07-04 2388
-
一种基于高效采样算法的时序图神经网络系统介绍2022-09-28 2815
-
隐藏技术: 一种基于前沿神经网络理论的新型人工智能处理器2022-03-17 15937
-
卷积神经网络一维卷积的处理过程2021-12-23 1786
-
一种基于综合几何特征和概率神经网络的HGU轴轨识别方法2021-09-15 1187
-
分享一种400×25×2的三层BP神经网络2021-07-12 1324
-
一种改进的深度神经网络结构搜索方法2021-03-16 1053
-
针对Arm嵌入式设备优化的神经网络推理引擎2021-01-15 2242
-
人工神经网络实现方法有哪些?2019-08-01 3421
-
一种基于模糊神经网络的机器人控制技术2016-09-19 2226
-
一种基于傅里叶基神经网络的频谱分析方法2009-11-11 720
-
一种基于人工神经网络的秘密共享方案2009-08-15 472
-
一种基于PID神经网络的解耦控制方法的研究2009-06-15 738
全部0条评论

快来发表一下你的评论吧 !

