快速傅里叶变换FFT进行串讲

本文对离散信号的频域分析（共5节）中的第4节——快速傅里叶变换FFT（Fast- Fourier Transform）进行串讲。

首先大家需要知道的是，FFT并不是一种新的变换，它仅仅是作为DFT的快速算法。本节包括下列内容：

4.1  改进DFT计算的方法

1. DFT计算量分析

观察正变换和反变换的公式可知，二者的运算方式和运算量是完全相同的。下面的分析均以DFT正变换为例。（顺便说一句，大家要像熟悉自己的手机一样熟悉旋转因子，闭着眼睛都知道它）

观察DFT正变换的公式，容易看出：每计算一个点的数据，需要N次复数乘法、N-1次复数加法，所以，N点DFT，需要N的平方次复数乘法，N(N-1)次复数加法。我们知道，DFT的点数，至少要取成序列的长度，当序列长度很长时，运算量巨大！如下图所示。

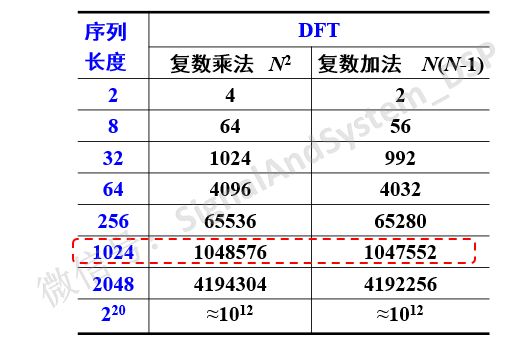
以1024点为例，复数乘法的次数100万次之多。

1965年，库利（J.W.Cooley）和图基（J.W.Tukey）在《Mathmatics of Computation》上发表了《AnAlgorithm for the Machine Calculation of Complex Fourier Series》，提出一种高效DFT运算的快速算法，后人称为快速傅里叶变换（Fast Fourier Transform ——FFT）。

2. 改进DFT计算效率的基本途径

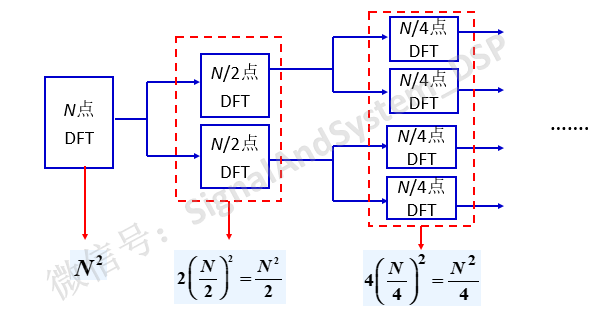
N点DFT，直接计算，需要N的平方次乘法；分成2个N/2点DFT分别计算，乘法的次数是1/2的N的平方，减少了一半；分成4个N/4点DFT，乘法的次数又减少了一半。如果能够继续下去，前景很让人向往。

为了能够一直分下去，我们限定N为2的整数次幂，即：N=2^M，称为基2FFT。

由此可见，FFT的基本思想是：把长序列分成几个较短的序列。

但怎么分？不能随便乱分，基本原则是：要保证这几个短序列的DFT组合起来后，能够很方便地构成原来长序列的DFT。

所以，DFT快速算法要解决的两个核心问题是：怎么分？怎么合？

根据分与合的方式不同，有两种基2FFT算法，分别称为：

按时间抽取的FFT算法——Decimation-in-Time，简称DIT-FFT。

按频率抽取的FFT算法——Decimation-in-Frequency，简称DIF-FFT。

下面我们分别来归纳总结两种基2FFT算法。

4.2  两种基2FFT算法

1. 按时间抽取（DIT）FFT算法

以第一次分解（N点分为2个N/2点）为例来说明算法原理。

首先解决怎么分的问题。

通俗地说，就是：大家列队、报数（从0开始）。报偶数的一组，奇数的一组。

然后解决怎么合的问题。

我们略过看似艰苦卓绝实际很简单的推导过程，直接上结论：

公式不好看，有人画了一幅图，并且起了个好听的名字：蝶形运算符号。

下面的动图演示了蝶形运算的过程：

以8点长序列为例，我们来看分解为2个4点长DFT，是如何通过蝶形运算合成8点DFT的：

经过第一次分解之后，总的运算量=两个N/2点DFT的运算+N/2个蝶形的运算。而每次蝶形运算，只需要1次乘法，2次加法。所以，总的乘法次数为

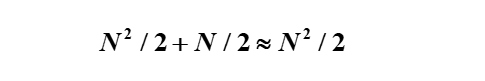
加法次数为

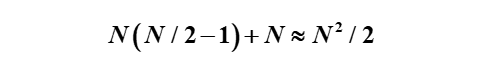
当N很大时，运算量减少了近一半。

这就给了我们信心，说明这种分解思路是可以有效减少运算量的。我们继续分解下去，经过M-1次分解，分解为N/2 个 2 点长序列。

而2点DFT也用蝶形运算来表示（因为计算机最擅长一致而重复的东西），就得到下面的流图：

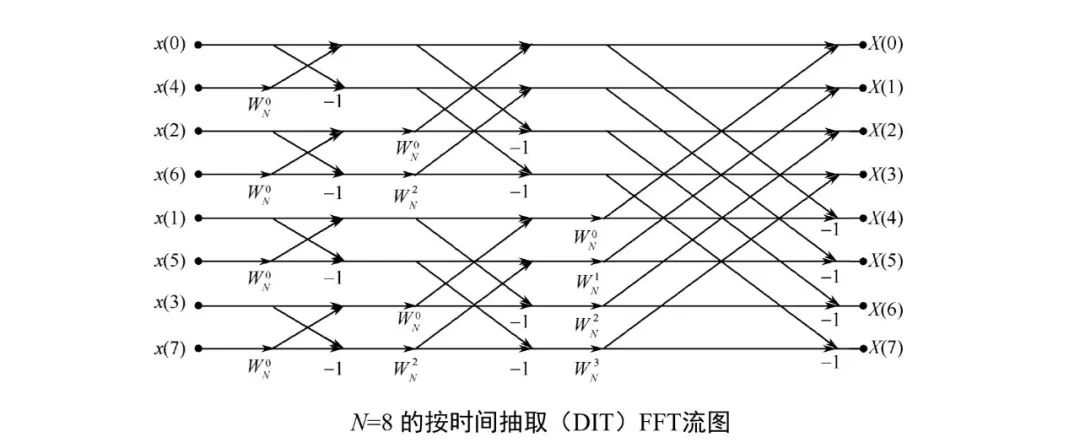
2. 按频率抽取（DIF）FFT算法

仍以第一次分解（N点分为2个N/2点）为例来说明算法原理。

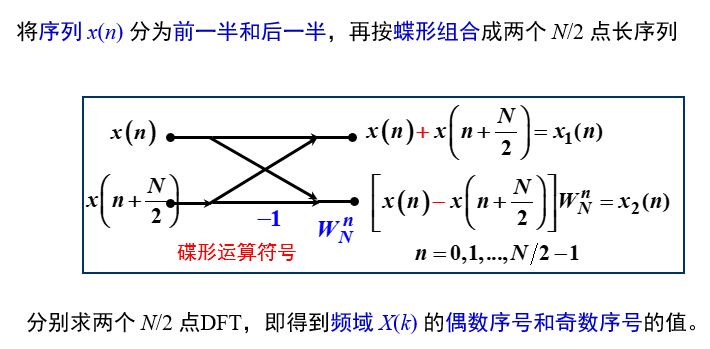
以8点长序列为例，我们来看分解为2个4点长DFT，是如何通过蝶形运算合成8点DFT的：

注意到，输出的频率数据，序号是按照偶数一组、奇数一组的顺序排列的，所以这种算法称为：按频率抽取。

我们继续分解下去，经过M-1次分解，分解为N/2 个 2 点长序列，就得到下面的流图：

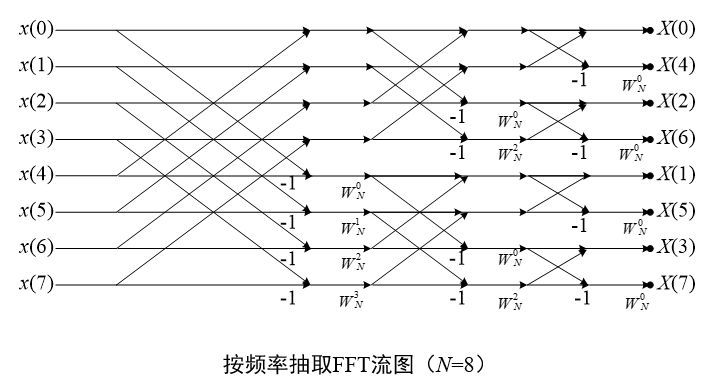
3. 运算量分析

通过前面的分析可见，两种基2FFT算法，运算量是一样的，N点DFT，就分解成了若干个蝶形的运算而已。

多少个蝶形呢？序列长度 N=2^M，共有 M级蝶形，每级N/2 个蝶形，共MN/2个。

而每个蝶形是1次复数乘法，2次复数加法。所以总的运算量为：

以N=1024=2^10为例，直接计算DFT，需要1024的平方=1048576

次乘法，而采用FFT只需要（1024/2）×10=5120次乘法，二者的比值为204.8。运算量减少了好几个数量级。

频率作为自然界的一个基本物理量，是很多领域研究的重要内容。人们很早就认识到，用DFT的方法可以有效进行信号的频率分析。但是因为DFT算法运算量很大，在数字计算机发明以前，运算效率普遍很低的情况下，DFT也更多的是一种理论分析工具，很难被用于实际的信号处理。

FFT的出现，破解了这一历史性难题，极大地促进了数字信号处理这门学科的应用和发展。有人甚至以FFT算法提出的1965年作为数字信号处理这门学科的诞生之年。

4. 算法特点

在计算机看来，这两种算法是非常相像的。

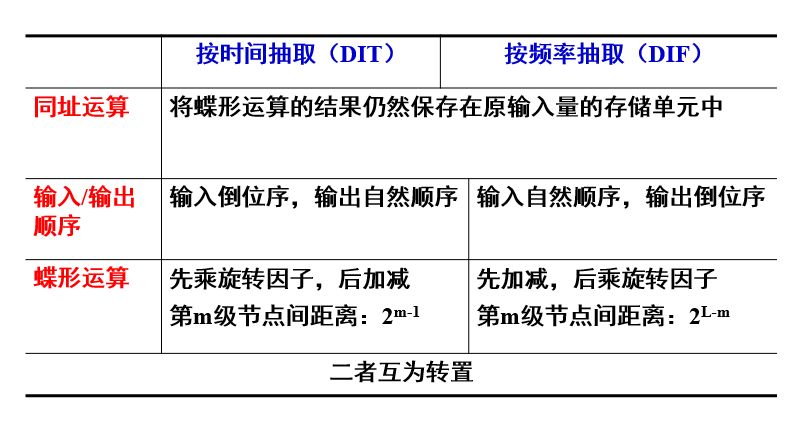
首先来看第一个特点：同址运算（又称同位运算或原位运算），每完成一个蝶形运算，输入的两个数据就没有用的，这就意味着，不需要再重新开辟新的存储单元来保存输出数据，计算结果仍保留在原输入数据占据的存储单元即可。

再来看第二个特点：输入/输出数据的顺序。这是两种算法的不同之处。以DIT-FFT为例来说明为什么会输入倒位序。

还是以8点长数据为例，输入数据的正常顺序是x(0)、x(1)、x(2)......x(7)，我们称之为 自然顺序。按照序号的奇偶分为两组，第一组是x(0)、x(2)、x(4)、x(6)，第二组是x(1)、x(3)、x(5)、x(7)。每个新的组再重新排队报数，按奇偶分，第一组又分成两个组，分别是x(0)、x(4)和x(2)、x(6)，第二组分成两个组，分别是x(1)、x(5)和x(3)、x(7)。

也就是说，8点长序列的DIT-FFT，输入数据的顺序是：x(0)、x(4)、x(2)、x(6)、x(1)、x(5)、x(3)、x(7)。这个序号的顺序乍看杂乱无章，其实有规律性。0、1、2、3、4、5、6、7的顺序与0、4、2、6、1、3、5、7有何关系的呢？用二进制来写一目了然，看下面的动图：

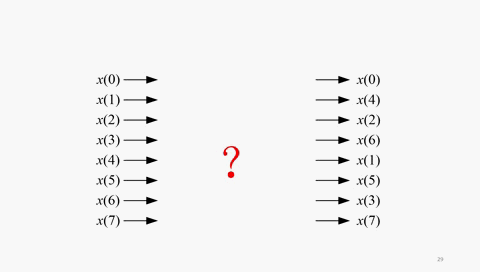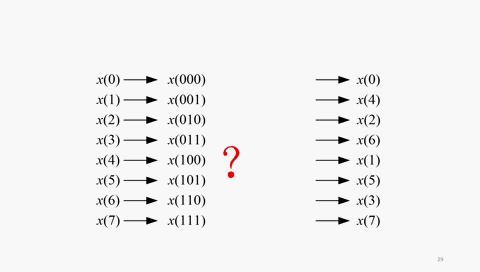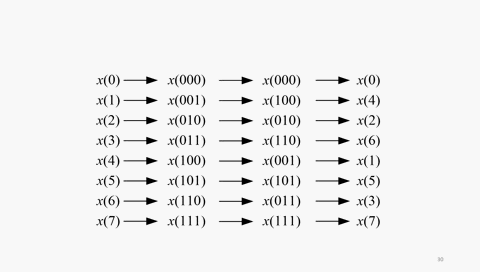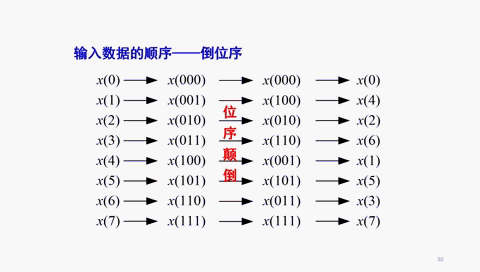
倒位序，是将二进制数的最高有效位到最低有效位的位序进行颠倒排列而得到的二进制数。 

DIT-FFT算法中，对时域序列按照序号的奇偶进行分解，造成输入序列的序号按照倒位序排列。

最后再说一说蝶形运算的规律。两种FFT算法，最终都是转换成了M列、每列N/2个、一共MN/2个蝶形运算。但二者蝶形运算的规律有差异。

第一个差异：基本蝶形不同。DIT是先乘旋转因子，再加或减；而DIF是先加或减，再乘旋转因子。

第二个差异：两种算法，蝴蝶翅膀的距离（即节点间的距离）和旋转因子的数目恰好相反。

仔细观察两种算法的流图，我们会发现，二者互为转置。

4.3 其他FFT算法简介

1. 混合基FFT

2. Chirp-z变换

实际应用中，有时只对信号的某一频段感兴趣，即只需要计算单位圆上某一段的频谱值，而不需要计算[0，Π]区间的所有频谱采样值。此时，可以用”Chirp-z变换“（CZT）。

适用场合：窄带信号的DFT。

3. Goertzel算法

在某些应用场合，只需计算很少几个频率点的频谱值。例如，双音多频信号（DTMF）的检测。此时可以采用卡泽尔（Goertzel）算法。

除此之外，傅里叶变换的快速算法还有很多种。不过应用最广泛的依然能是基2FFT算法，它是数字信号处理最经典算法之一，几乎各种主流的计算机编程语言都有现成的函数可以调用。不同型号的芯片，硬件开发商也都会给出优化后的FFT算法源代码，一般情况下直接调用就可以。