基于条件概率分类的两种模型算法：logistic回归模型与最大熵模型。

条件概率是机器学习模型的一种表现形式，应用这一模型，对于给定的输入X，得到各输出类的概率，选择最大概率的类为输出类，如下图：

本文介绍基于条件概率分类的两种模型算法：逻辑斯蒂（logistic）回归与最大熵模型，其中，logistic回归模型和最大熵模型分别是基于最大似然函数和熵来估计模型P(y|x)。公众号已有logistic回归模型的文章介绍，本文重点分析最大熵模型算法。

目录

1. 最大熵模型算法

2. 最大熵模型例子

3. 最大熵模型在信号检测的应用

4. logsitic回归模型算法

5. 总结

1.最大熵模型算法

熵是衡量随机变量不确定性的指标，熵越大，随机变量的不确定性亦越大。假设X是一个离散型随机变量，其概率分布为：

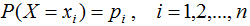
随机变量X的熵定义为：

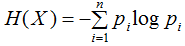
熵满足下列不等式：

式中，|X|是x的取值个数，当且仅当X的分布是均匀分布时，右边的等号成立，也就是说，当X服从均匀分布时，熵最大。

1.1 最大熵模型的定义

最大熵原理是概率模型学习的一个准则，最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。条件概率是机器学习模型的一种表现形式，学习该模型的一种方法是最大化该条件概率的熵 ，即最大化下式：

其中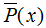表示变量X的经验分布：

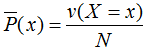
其中v(X=x)表示训练数据中输入x出现的频数，N表示样本容量。

（1）式的未知变量就是需要学习的模型。

我们在构建分类模型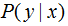的过程中假设训练数据集的联合概率分布与真实模型的联合概率分布相等，这一假设用特征函数f(x,y)的期望来描述，特征函数的定义：

特征函数f(x,y)关于训练数据集的联合概率分布的期望值，用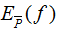表示：

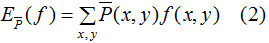
其中，

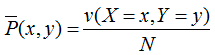
，v(X=x,Y=y)表示训练数据中样本(x,y)出现的频数。

特征函数f(x,y)关于模型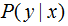与经验分布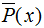的期望值，用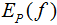表示：

假设两者期望相等，即：

或

结合(1)(4)式，得到最大熵模型：

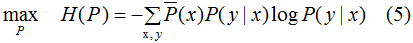
约束条件：

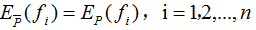
1.2 最大熵模型的学习

我们求解(5)式在约束条件下的最大值，其对应的模型P(Y|X)就是所学习的最优模型。

对于给定的训练数据集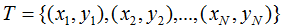以及特征函数，i=1,2,...,n，最大熵模型的学习等价于约束最优化问题：

将最大值问题转化为等价的求最小值问题：

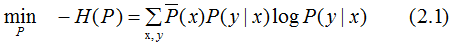
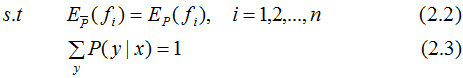
引入拉格朗日乘子将约束的最优化问题转换为无约束最优化的对偶问题，通过求解对偶问题求解原始问题。

定义拉格朗日函数L(P,w)：

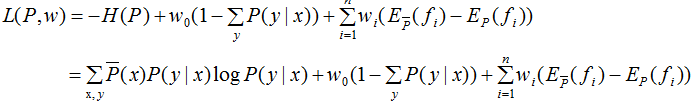
最优化的原始问题：

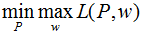
对偶问题：

令

得：

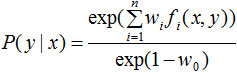
由于，对上式进行归一化得：

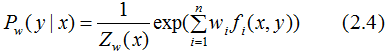
其中，

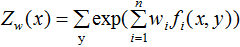
令

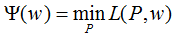
易知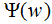对偶问题外部的极大化问题：

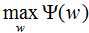
根据上式求解的代入(2.4)式，得到最终的学习模型P(y|x)。

2. 最大熵模型例子

假设随机变量Y有5个取值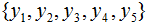，假设随机变量Y的条件概率分布满足如下条件：

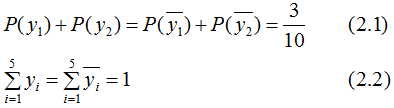
求最大熵模型对应的概率分布P(Y)。

最大熵模型的目标函数：

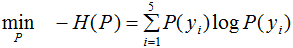
引进拉格朗日乘子，定义拉格朗日函数：

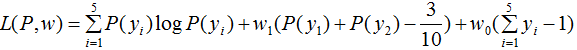
令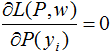，得：

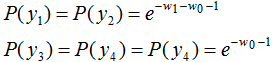
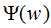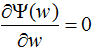将上式代入函数L(P,w)得，令，得：

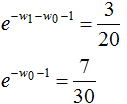
于是最大熵模型对应的概率分布：

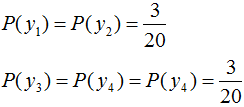
3. 熵模型在信号检测的应用

由第一节我们知道，熵是描述事物不确定性的指标。我们将熵的这一性质应用在信号检测领域，当信号包含了较强的随机噪声时或被噪声完全掩盖时，信号的随机性大大的增加了，其对应的熵也较大，根据这一原理对信号的质量进行检测，下图是用熵检测心电信号质量的效果图：

黑色表示较好的心电信号质量，红色表示较差的心电信号质量。

4. logistic回归算法

logistic回归是一种概率分类模型，对于二分类任务来说，其条件概率分布：

我们用最小化损失函数去估计上式的模型参数。对于给定的训练数据集，其中，。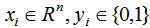

设：

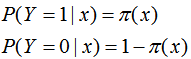
似然函数为：

对数似然函数为：

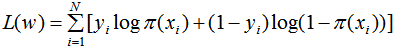
损失函数为：

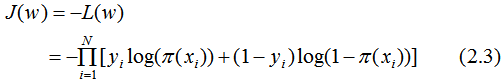
用梯度下降法求解w的估计值：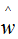

代入（2.1）（2.2）式，得到逻辑斯蒂回归模型P(y|x)，其中向量包含了b值 。

5. 小结

本文介绍基于条件概率分类的两种模型算法：logistic回归模型与最大熵模型，其中，logistic回归模型是基于最大似然函数估计模型P(y|x)，最大熵模型是基于熵这一指标估计模型P(y|x)。