离散信号的频域分析之傅里叶变换的应用

本文是离散信号的频域分析（共5节）中的第5节——傅里叶变换的应用的第一篇。

在开始学习之前，提醒大家，本节内容的学习，需要用到前面DTFT、DFT以及FFT的知识。如果前面这些内容没有掌握的话，那就不具备继续学习本节内容的条件。当然，本节内容的学习，可以加深对前面这几个问题的深化理解。

本节内容分为两部分：5.1 FFT分析信号频谱；5.2 FFT实现线性卷积。本文是第一部分：FFT分析信号频谱。

5.1  FFT分析信号频谱

1. 用FFT实现频谱分析的基本过程

我们知道，现实世界中的绝大多数物理量都是以连续变化的形式存在的，而做为离散傅里叶变换，只能处理有限长的离散数据。所以对信号进行FFT之前，必须首先将其进行离散化处理并截取合适的长度。

下图为用FFT实现频谱分析的基本过程。

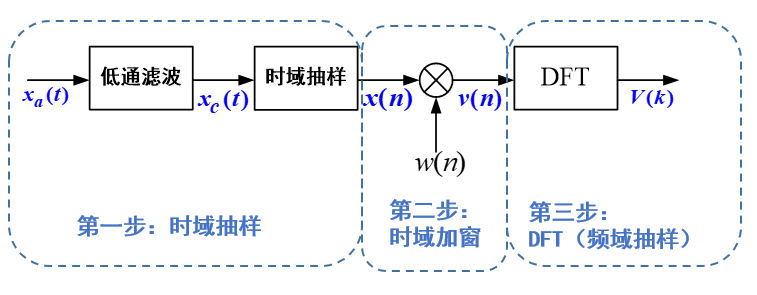
下面我们详细来看具体每一步对信号做了什么样的处理，我们重点关注这些处理对信号的频谱特征有什么样的影响。

2. 时域抽样

第一步为时域抽样，我们已经学习过。其作用是将连续时间信号按照一定的抽样间隔离散化，得到离散数据。时域抽样包含两个过程：

首先，将连续时间信号通过理想低通滤波器，该滤波器又称为“抗混叠滤波器”，作用是滤除高于抽样频率一半的高频分量，防止抽样时发生频谱混叠。

然后，对信号进行抽样。抽样后得到离散时间信号x(n)，其频谱，能否代表原来的连续时间信号的频谱信息呢？

当然能！因为只要满足抽样定理，抽样后的离散数值就可以完全代表原来连续时间信号的信息。但问题是，离散时间信号的频谱，已经是数字域频率，携带的频率信息，需要转换为模拟频率，如何转换？

这个问题，本公号前面有文章专门论述，链接如下：

数字信号处理系列（离散信号的频域分析之二）——数字域频率与模拟角频率

本文不再重复，只给出结论。

根据上图的公式反推：

模拟角频率 = 数字域频率 * 抽样频率fs

3. 时域加窗

下面我们分析第二步——时域加窗。

从三个方面来看：第一，为什么要加窗？第二，怎样实现加窗？第三，加窗有什么影响？

首先看，为什么要加窗？无他，因为数据太长太多，处理不了啊，臣妾做不到；或者是处理时间太长，臣妾等不及啊。更有甚者，有时输入信号是无限长的，总不能等到世界末日再去处理吧？

然后看，怎样实现加窗？

最简单加窗方式，就是将很长很长的数据，与矩形脉冲RN(n)相乘，就实现了截取n=0~N-1这N个点。RN(n)称为“矩形窗”。

除了矩形窗，有没有其他形式的窗呢？有，但这是后话，以后再讲。

这里重点分析第三个问题——加窗有什么影响？

先看一般的信号，如下图所示，频谱为示意图。根据“时域相乘，频域卷积”，加窗后信号的频谱，是原来的频谱X(w)与矩形窗的频谱W(w)做卷积，那么，卷积后的频谱（也即加窗后的频谱）是什么样子呢？和很多因素有关（原始信号的频谱、窗函数的频谱、长度等等）。从何处入手来分析呢？

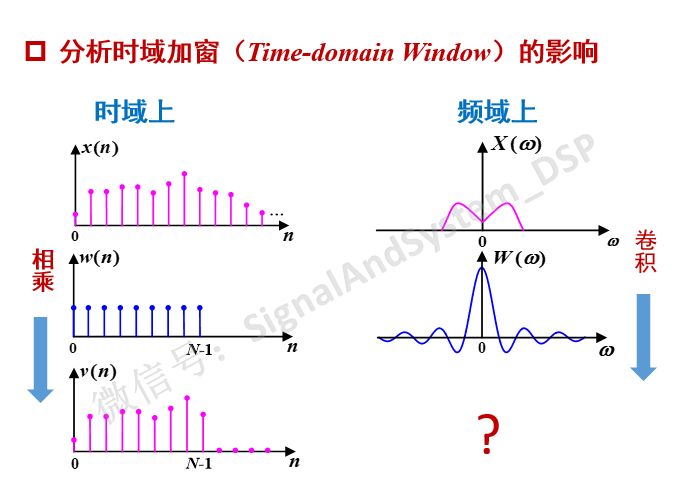
我们知道，正弦信号是基本信号，因为复杂信号可以看是一个个不同频率的正弦信号组合而成，所以下面首先分析正弦信号。

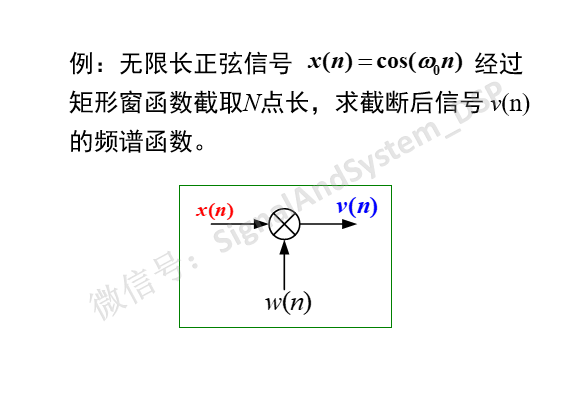
我们知道，无限长正弦信号的频谱为正负w0处的冲激，如下图（a），矩形窗的频谱，如下图（b）。二者卷积后（也就是N点长的正弦信号）的频谱，如图（c）。

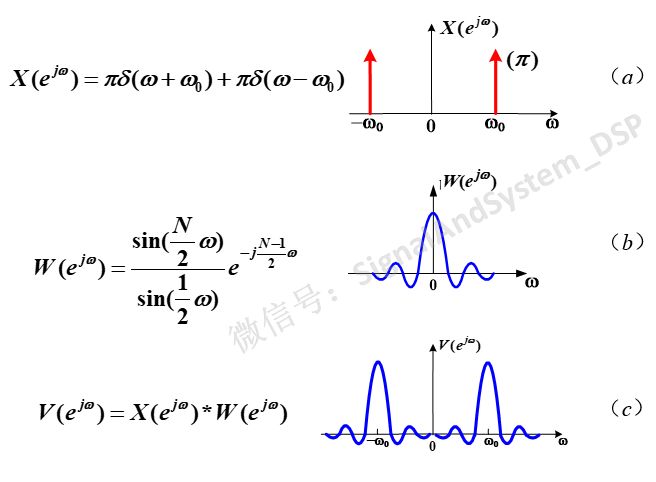
比较图（a）和图（c），可以看到，加窗后信号的频谱与加窗前相比，发生了哪些变化呢？变宽了，原来窄窄的一条（瘦成闪电）变成宽宽的胖子，而且出现起伏的尾巴。

用术语说，就是：

时域加窗，导致频谱的扩散——拖尾、变宽，称为频谱泄漏（ Leakage ）。

为什么变胖？是因为矩形窗函数的频谱胖（主瓣）。胖的程度，取决于N。N越小主瓣越宽，则越胖。所以，我们要想减少主瓣泄露，可以适当增大N。

为什么出现尾巴？是因为矩形窗函数的频谱有起伏（旁瓣）。要想减小旁瓣泄露，就要降低窗函数旁瓣的幅度。

但是，我们知道，矩形窗函数，旁瓣幅度与主瓣幅度之比是一定的（-13dB左右），增大N并不能改变这一数值。那么，如何是好呢？

对数据加矩形窗是我们很自然的行为，因为它不改变截取部分信号的取值。但是矩形窗在起点和终点都是不连续的，也就是说，数据是突然开始、突然结束的。从物理概念上很好解释，这种时域上的突然变化，意味着频域上存在高频分量。如果抑制了这些高频分量，就能够降低旁瓣幅度。因此从这样一个角度，直观上就可以想到，窗函数的起始处和结束处越平坦，对旁瓣的抑制就应该越好。关于窗函数的内容，我们后面会专门学习。

前面分析了加窗对信号频谱的影响，总结一句话：时域加窗，会导致频谱泄露——频谱展宽、拖尾。同时，我们必须认识到，在进行DFT运算时，时域加窗是必须的，因此泄漏现象是离散傅里叶变换所固有的，无法消除，只能在计算量等容许的范围内，尽量抑制泄露现象。 

4. 频域抽样（DFT）

经过前面两步，数据离散化了，也是有限长的了，准备工作终于完成了，可以做DFT了。

DFT，也就是频域抽样。其实质就是对信号v(n)的频谱（DTFT）离散化，[0，2Π]区间上离散化成N个点，就是N点DFT。注意，这个N是指DFT的点数，而不是前文中的信号长度。

v(n)的频谱也就是上图中的（c），但我们首先需要把图（c）变一下。

为什么需要变一下呢？所有离散时间信号的频谱，都是以2Π为周期的，图（a）（b）（c）实际上画出的是-Π~Π区间内的图形。为了和DFT的研究区间一致（[0，2Π]），我们把图（c）变成[0，2Π]区间，也就是下图（d）。

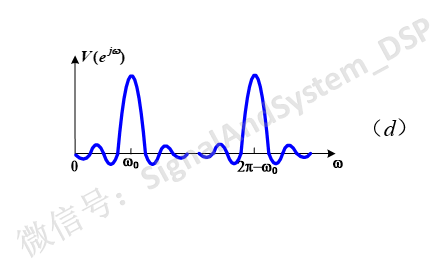
然后，把它以2Π/N为间隔离散化，得到的就是最后的结果V(k)。如下图（e）所示。

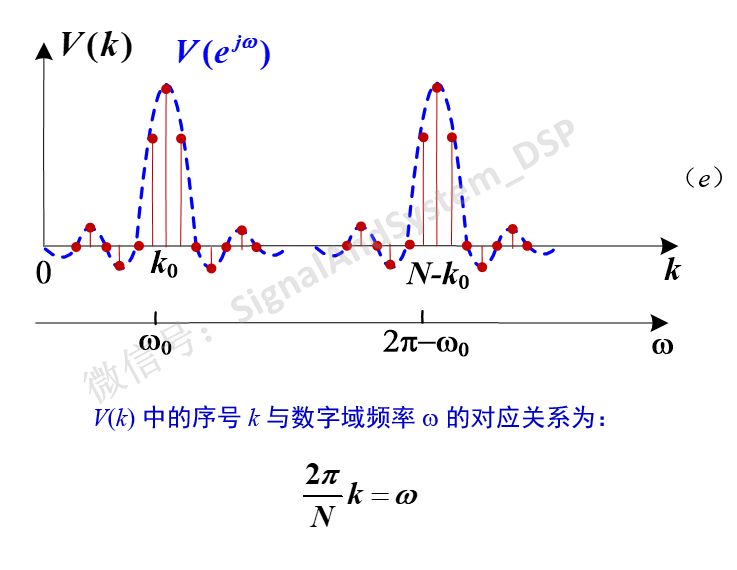
理论分析讲完了，最后出一个题。