决策树和随机森林模型

这是一个系列教程，试图将机器学习这门深奥的课程，以更加浅显易懂的方式讲出来，让没有理科背景的读者都能看懂。

前情提要：这是一个系列教程。如果你刚好第一次看到这篇文章，那么你可能需要收藏一下本篇文章，然后先看一下这个系列的前一篇《文科生都能看懂的机器学习教程：梯度下降、线性回归、逻辑回归》。如果你已经看过了，那么就不再多说，让我们继续吧。

本次主要讲的是决策树和随机森林模型，

决策树

决策树是个超简单结构，我们每天都在头脑中使用它。它代表了我们如何做出决策的表现形式之一，类似if-this-then-that：

首先从一个问题开始；然后给出这个问题的可能答案，然后是这个答案的衍生问题，然后是衍生问题的答案…直到每个问题都有答案。程序员和PM应该这个流程非常熟悉的。

先看一个决策树的例子，决定某人是否应该在特定的一天打棒球。

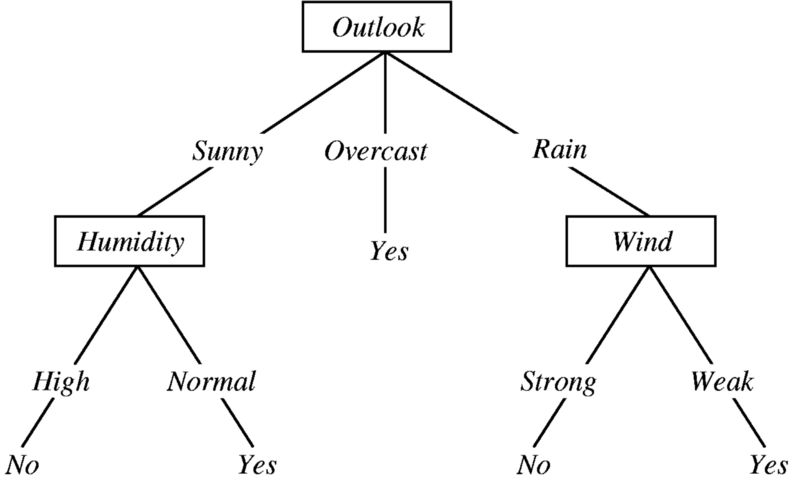
图片来源：Ramandeep Kaur的 “ 机器学习与决策树”

这棵树从上往下，首先提出一个问题：今天的天气预期如何？接下来会有三种可能的答案：晴；阴；雨。

1. if 天气=晴天，那么判断湿度如何

1. if 湿度高，then 取消

2. if 湿度低，then 去玩

2. if 天气=阴天，then 去

3. if 天气=下雨，then 取消

一棵简单的决策树就出来了。决策树具备以下特性：

决策树用于建模非线性关系（与线性回归模型和逻辑回归模型相反）

决策树可以对分类和连续结果变量进行建模，尽管它们主要用于分类任务（即分类结果变量）

决策树很容易理解！ 您可以轻松地对它们进行可视化，并准确找出每个分割点发生的情况。 您还可以查看哪些功能最重要

决策树容易过拟合。这是因为无论通过单个决策树运行数据多少次，因为只是一系列if-this-then-that语句，所以总是会得到完全相同的结果。这意味着决策树可以非常精确地适配训练数据，但一旦开始传递新数据，它可能无法提供有用的预测

决策树有多种算法，最常用的是ID3（ID代表“迭代二分法”）和CART（CART代表“分类和回归树”）。这些算法中的每一个都使用不同的度量来决定何时分割。ID3树使用信息增益 ，而CART树使用基尼指数 。

ID3树和信息增益

基本上ID3树的全部意义在于最大限度地提高信息收益，因此也被称为贪婪的树。

从技术上讲，信息增益是使用熵作为杂质测量的标准。好吧。我们先来了解一下熵。

简单地说，熵是（dis）顺序的衡量标准，它能够表示信息的缺失流量，或者数据的混乱程度。缺失大量信息的东西被认为是无序的（即具有高度熵），反之则是低度熵。

举例说明：

假设一个凌乱的房间，地板上是脏衣服，也许还有一些乐高积木，或者switch、iPad等等。总之房间非常乱，那么它就是熵很高、信息增益很低。

现在你开始清理这个房间，把散落各处的东西意义归类。那么就是低熵和高信息增益。

好，回到决策树。ID3树将始终做出让他们获得最高收益的决定，更多信息、更少的熵。

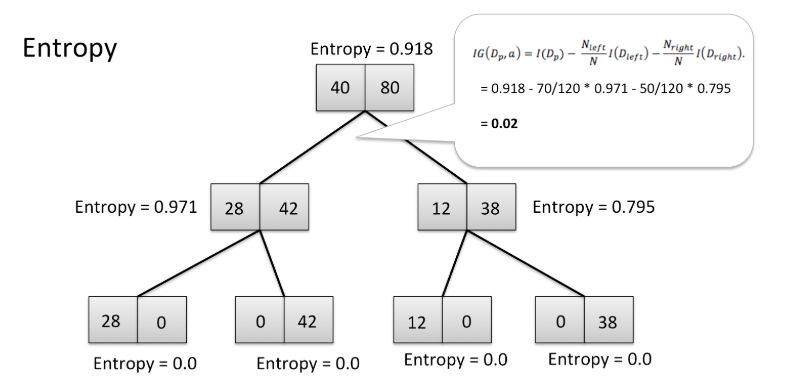
在决策树中的可视化的熵

在上面的树中，你可以看到起始点的熵为0.918，而停止点的熵为0.这棵树以高信息增益和低熵结束，这正是我们想要的。

除了向低熵方向发展外，ID3树还将做出让他们获得最高纯度的决定。 因为ID3希望每个决定都尽可能清晰，具有低熵的物质也具有高纯度，高信息增益=低熵=高纯度。

其实结合到现实生活中，如果某些事情令人困惑和混乱（即具有高熵），那么对该事物的理解就会是模糊的，不清楚的或不纯的。

CART树和基尼指数

和ID3算法不同，CART算法的决策树旨在最小化基尼指数。

基尼指数可以表示数据集中随机选择的数据点可能被错误分类的频率。 我们总是希望最小化错误标记数据可能性对吧，这就是CART树的目的。

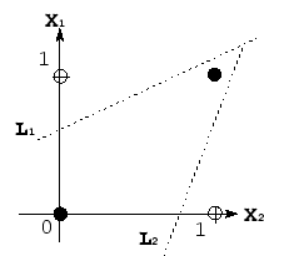
线性模型下线性函数的可视化

随机森林

随机森林可以说是初学数据科学家最受欢迎的集合模型。

集合模型顾名思义。是许多其他模型的集合。

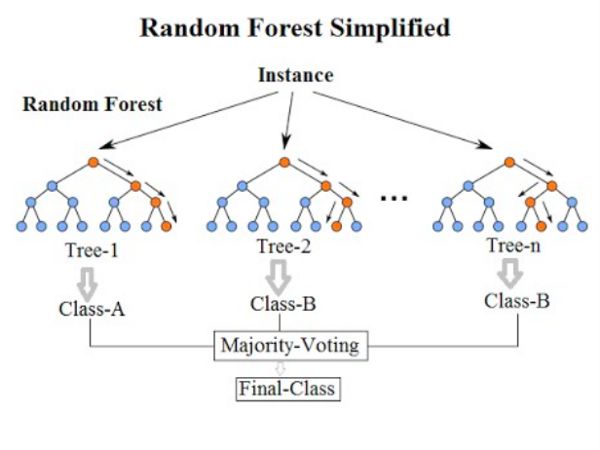
来自KDNuggets的随机森林结构。

正如你在左边的图表中看到的3个决策树，像Random Forest这样的集合模型只是一堆决策树。

像随机森林这样的集合模型，旨在通过使用引导聚集算法（装袋算法）来减少过度拟合和方差。

我们知道决策树容易过拟合。换句话说，单个决策树可以很好地找到特定问题的解决方案，但如果应用于以前从未见过的问题则非常糟糕。俗话说三个臭皮匠赛过诸葛亮，随机森林就利用了多个决策树，来应对多种不同场景。

然而在数据科学领域，除了过度拟合，我们还要解决另一个问题叫做方差。具有“高方差”的模型，尽管输入最微小的位改变，其结果也会有很大的变化，类似于失之毫厘谬以千里，这意味着具有高方差的模型不能很好地概括为新数据。

装袋算法

在深入研究随机森林依赖的装袋算法之前，仍然了解一个概念：learner。

在机器学习中，分为弱learner和强learner，装袋算法主要用于处理弱learner。

弱learner

弱learner构成了随机森林模型的支柱，它是一种算法，可以准确地对数据进行预测/分类！

像随机森林这样的集合模型使用装袋算法来避免高方差和过度拟合的缺陷，而单个决策树等更简单的模型更容易出现。

当算法通过随机数据样本建立决策树时，所有数据都是可以被利用起来的。

综上所述： 随机森林模型使用装袋算法来构建较少的决策树，每个决策树与数据的随机子集同时构建。

随机森林模型中的每个树不仅包含数据的子集，每个树也只使用数据的特征子集。

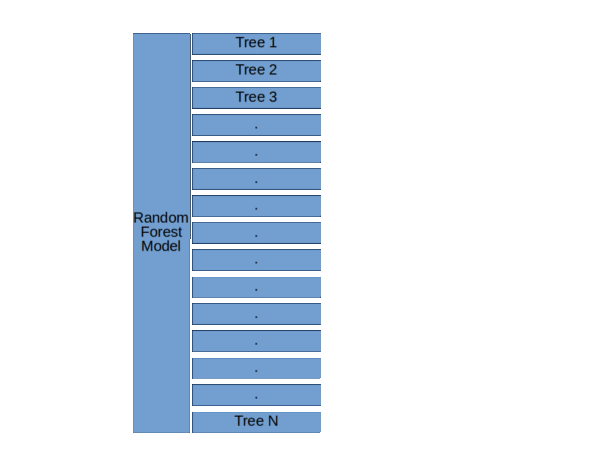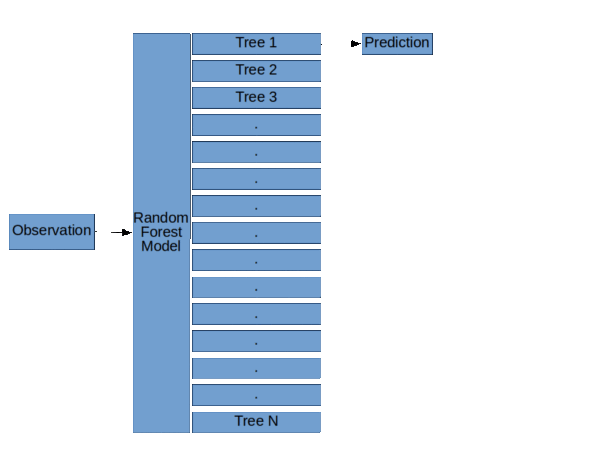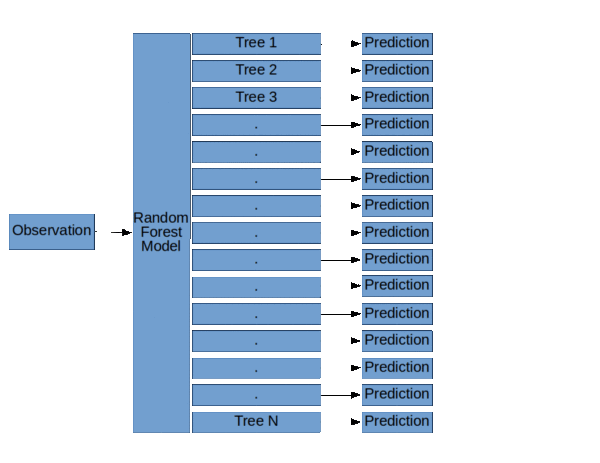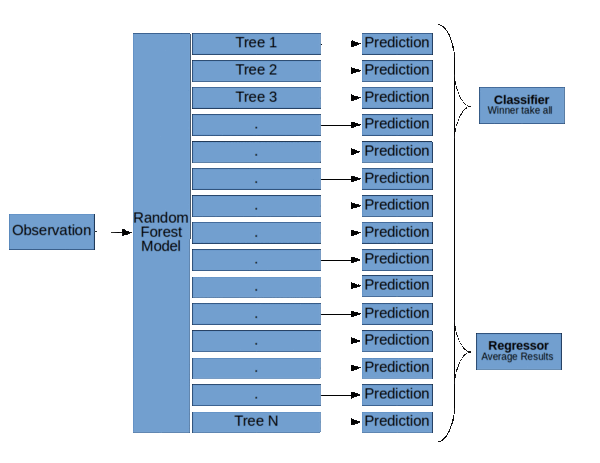
随机森林模型的基本结构（ 随机森林，决策树和集合方法由Dylan Storey 解释 ）

通过这篇文章，我们学习了所有关于决策树、过度拟合和方差以及随机森林等集合模型。第三部分将介绍两个线性模型：SVM和朴素贝叶斯。