

在重费米子体系中发现外尔费米子激发
电子说
描述
凝聚态物质中的拓扑序和拓扑相变是物理学中的一个重要发现,它突破了基于对称性破缺的经典朗道理论,解释了包括涡旋激发、量子霍尔效应等在内的许多新现象。近年来,人们在凝聚态材料中发现了一系列受对称性保护的拓扑量子物态,例如拓扑绝缘体、狄拉克半金属、外尔半金属等[1—4]。这些拓扑材料表现出独特的电子性质,在自旋电子器件以及量子计算等方面具有独特的应用前景。寻找新型拓扑材料、揭示新的拓扑物性仍是当今前沿热点研究问题。
外尔半金属是一类重要的拓扑半金属材料,由于其准粒子低能激发与外尔费米子具有类似的性质而得名。1929 年,赫尔曼·外尔(Hermann Weyl)通过对狄拉克方程做了零质量简化,得到了所谓的外尔方程,其描述的就是质量为零且具有自旋手性的外尔费米子[5]。寻找外尔费米子一直是高能物理领域中的一个重要课题,然而迄今尚未在实验上找到相应的粒子。近年来,人们在一些凝聚态物质的电子结构中发现成对出现的外尔点,这些外尔点在表面上的投影由费米弧连接,即一段不闭合的费米面[4]。外尔半金属表现出许多新奇电学特性,例如线性巨磁阻、手性反常效应和反常霍尔效应等。
迄今为止,绝大部分实验中确认的外尔半金属均属于弱关联电子体系。在这些材料中,由于电子间关联效应较弱,第一性原理计算往往能比较准确地预言其能带结构和拓扑性质,并且能被角分辨光电子能谱等实验证实。那么,强关联电子体系中是否也存在外尔费米子?电子关联效应与拓扑序相结合后会产生什么新的现象?怎样来探测强关联电子体系中的拓扑性质?
重费米子是一类典型的强关联电子体系,通常存在于含有f 电子的镧系或者锕系金属间化合物中[6—8]。在重费米子体系中,随着温度的降低,局域的f 电子通过近藤效应与导带电子集体杂化而产生巡游的重电子,其有效质量可高达自由电子质量的上千倍,“重费米子”因此而得名。在这类材料中,局域电子与巡游电子间的近藤相互作用还会打开一个小的杂化能隙。当费米能级位于杂化能隙之内时,材料呈现出绝缘体或者半导体行为,这类材料又称近藤绝缘体或者半导体(图1(b))。而在更多的情况下,费米能级穿过导带或价带,材料表现出金属行为(图1(c))。因此,重费米子体系可以呈现出非常丰富的量子特性。1979年,德国科学家Frank Steglich 教授(现为浙江大学关联物质研究中心主任)首次在重费米子金属CeCu2Si2中发现超导,这也是第一个非常规超导体[9]。到目前为止,人们已经在40 多个重费米子材料中观察到超导现象。重费米子超导表现出许多与高温超导相似的性质,对研究高温超导机理具有重要借鉴意义。另一方面,由于重费米子体系的特征温度(例如超导转变温度、磁性相变温度和近藤温度等)都比较低,其基态连续可调,因而是研究量子相变的理想体系。

图1 传导电子与局域电子(a),在低温下杂化形成近藤绝缘体(b)或者近藤金属(c)
近年来,人们一直致力于在重费米子材料中寻找拓扑量子态。当重费米子材料的局域f 电子与传导电子能带具有不同的宇称(或更一般地,属于同一对称性的不同表示时),其近藤相互作用会打开一个杂化能隙,导致f 电子与传导电子的能带发生反转,在费米面附近出现受拓扑保护的表面态。然而,由于电子的多体相互作用以及f 电子的窄能带特性等因素,重费米子体系中的拓扑态研究也要比弱关联电子体系复杂得多。
在已知的材料中,SmB6被认为是一个潜在的拓扑近藤绝缘体。该材料具有高对称的立方晶体结构,并且在费米能附近只有d 电子和f 电子能带。最近的一系列实验表明,SmB6中存在表面金属态,如样品厚度对输运性质的影响[10],角分辨光电子能谱[11],扫描隧道显微镜[12]以及非局域输运性质测量[13]等。另一方面,该材料表现出独特的量子振荡行为[14,15],目前其机制尚存在争议。除了SmB6以外,最近人们在YbB12[16]、CeNiSn[17]等近藤晶格材料中也观察到了拓扑表面态的迹象。
类似于拓扑近藤绝缘体,人们也一直在重费米子体系中探索是否存在近藤狄拉克或者外尔半金属。理论计算表明,重费米子半金属CeRu4Sn6的能带结构中可能存在8—12 对外尔点[18],但由于其能带结构的复杂性,这一理论预言尚未被实验佐证。最近的低温比热测量表明,重费米子半金属Ce3Bi4Pd3 的能带可能存在外尔点[19]。然而,在分析低温电子比热时,该文章引入了一些假设,因而Ce3Bi4Pd3 的拓扑性质仍有待进一步确认。寻找新型拓扑近藤半金属材料,研究电子关联效应对外尔点的影响以及可能诱导的新物理现象,亟待更多的实验和理论研究。
从字面意思来看,重费米子和外尔费米子的概念似乎是矛盾的。外尔费米子在理论上来说是没有质量的,而重费米子的有效质量却很重。一个没有质量的粒子又怎么会“重”呢?实际上,外尔费米子的“零质量”是指一种独特的能量—动量色散关系:在外尔点附近,外尔费米子的能量与它的波矢成正比关系,其比例系数也即费米速度是个常数。在重费米子材料中,虽然电子有效质量大,费米速度小,但重费米子能带同样可以遵循线性色散关系。
理论上讲,寻找近藤外尔半金属有两种可能的途径。第一种方法是在一个存在外尔点的半金属材料中,通过适当的方法引入近藤效应而使能带重整化,从而得到近藤外尔半金属相。另一种可能的方法是在近藤半金属/半导体材料中,通过调节电子相互作用以及自旋—轨道耦合强度等参数,实现能带的拓扑转变,从而得到近藤外尔半金属相。
YbPtBi 是一个典型的重费米子半金属材料[20]。通过多种宏微观物性测量并结合能带计算,我们首次在该材料体系中发现了外尔费米子的实验证据,观察到外尔电子态随电子相互作用变化所呈现出来的一些新颖性质[21]。
在高温区间,4f 电子是局域的,与周围的巡游电子杂化比较弱,类似于弱关联电子材料。角分辨光电子能谱测量与能带计算的结果表明,该材料的能带结构中存在三重简并点,并且位于费米能级附近(图2(a))。在外加磁场下,这些三重简并点将进一步劈裂,从而形成外尔点。通过转角磁阻测量,我们也证实了外尔点的存在,观测到了明显的手性反常效应。
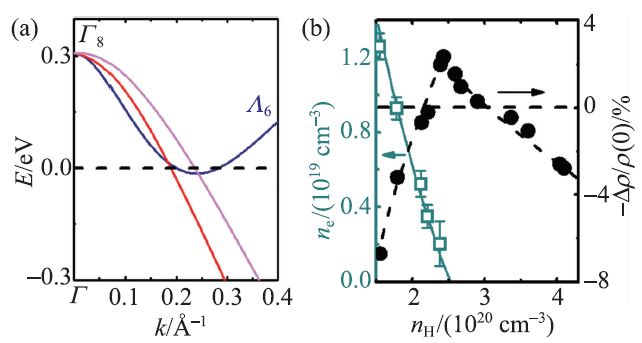
图2 YbPtBi 的高温拓扑性质[21] (a)沿着ΓL 方向的能带结构示意图;(b)载流子浓度与径向负磁阻之间的关系
此外,我们还系统地研究了径向电阻手性反常效应随样品载流子浓度的变化[22]。通过改变材料的生长条件,包括调节助溶剂Bi 的比例或者通过Au 元素的掺杂等,成功制备了一批具有不同载流子浓度的样品,得到了径向负磁阻效应与样品载流子浓度之间的关系,发现径向负磁阻仅出现在电子型载流子的临界阈值附近(图2(b)),与我们能带计算的结果一致,进一步表明YbPtBi 的径向负磁阻是由手性反常效应导致的,外尔点出现在费米能附近。
随着温度的下降,局域的f 电子与巡游电子杂化增强,形成有效质量很重的复合费米子,导致其费米速度迅速下降。与之相应,手性反常效应对径向磁阻的贡献迅速减少,在20 K以下可以忽略。由于近藤温度较低,目前的角分辨光电子能谱的能量分辨率还不足以揭示重费米子态中的能带拓扑结构。另一方面,重费米子体系的电子比热系数很大,有利于精密测量比热随温度的变化。通过低温比热测量,我们发现电子比热系数正比于温度的二次方(图3(a)),与具有线性色散关系的外尔点一致。此外,还在30 K以下观察到了明显的拓扑霍尔效应(图3(b)),进一步表明非平庸拓扑态的存在。

图3 YbPtBi 的低温拓扑性质[21] (a)比热Cp与温度T 的三次方依赖关系;(b)不同温度下的拓扑霍尔效应
我们的实验结果首次表明,在重费米子体系中存在外尔费米子激发,并且电子的关联效应可以调节外尔费米子的性质(图4),产生不同于弱关联外尔半金属的奇异行为。这些发现为研究具有近藤相互作用的外尔费米子半金属提供了一个范例,为研究拓扑态与电子关联效应和拓扑量子相变提供了一个新的平台,进一步表明强关联电子体系蕴藏的丰富物理内涵。

图4 外尔费米子随杂化强度演化的示意图(a)当局域电子(红色)与传导电子(蓝色)杂化较弱时,传导电子能带中存在外尔点;(b)随着杂化强度的增强,能带发生重整化,电子有效质量增加,外尔点仍然保留,但杂化后形成的准粒子的费米速度急剧减少
参考文献
[1] Hasan M Z,Kane C L. Reviews of Modern Physics,2010,82:3045
[2] Haldane F D M. Reviews of Modern Physics,2017,89:040502
[3] Qi X L,Zhang S C. Reviews of Modern Physics,2011,83:1057
[4] Armitage N P,Mele E J,Vishwanath A. Reviews of Modern Physics,2018,90(1):015001
[5] Weyl H. Proceedings of the National Academy of Sciences,1929,15:323
[6] Stewart S G R. Reviews of Modern Physics,1984,56(4):755
[7] Weng Z F,Smidman M,Jiao L et al. Reports on Progress in Physics,2016,79:094503
[8] Steglich F,Wirth S. Reports on Progress in Physics,2016,79:084502
[9] Steglich F et al. Physical Review Letters,1979,43:1892
[10] Syers P,Kim D,Fuhrer M S et al. Physical Review Letters,2015,114:096601
[11] Denlinger J D,Allen J W,Kang J S et al. Proceedings of the International Conference on Strongly Correlated Electron Systems (SCES2013),2014,1:017038
[12] Jiao L,Rößler S,Kim D J et al. Nature Communications,2016,7:13762
[13] Kim D J et al. Scientific Reports,2013,3:3150
[14] Li G,Xiang Z,Yu F et al. Science,2014,346(6214):1208
[15] Tan B S,Hsu Y T,Zeng B et al. Science,2015,349(6245):287
[16] Weng H,Zhao J,Wang Z et al. Physical Review Letters,2014,112:016403
[17] Chang PY et al. Nature Physics,2017,13(8):794
[18] Xu Y et al. Physical Review X,2017,7:011027
[19] Dzsaber S et al. Physical Review Letters,2017,118:246601
[20] Fisk Z et al. Physical Review Letters,1991,67:3310
[21] Guo C Y et al. Nature Communications,2018,9:4622
[22] Guo C Y et al. AIP Advances,2018,8:101336
- 相关推荐
- 热点推荐
- 电子
-
费米显卡驱动不再更新,32位系统不再是NVIDIA的主流2018-06-26 1659
-
专家首次发现马约拉纳费米子,人类或将迎来量子时代2020-04-12 2023
-
中科大首次发现拓扑外尔半导体,为新型拓扑半导体器件设计提供新思路2020-05-18 3901
-
AI新药公司费米子科技完成累计上亿元A轮融资2020-11-12 1934
-
诺奖得主团队在石墨烯研究上有新发现,可促进电子器件发展2020-11-19 2972
-
实验证实任意子存在,为费米子玻色子外另一基本粒子2020-12-24 1233
-
费米气体和超导是什么关系呢?费米子的代码让电阻消失了?2024-04-26 1596
全部0条评论

快来发表一下你的评论吧 !

