

常用的三种机器学习优化算法介绍和比较
电子说
描述
在本文中,作者对常用的三种机器学习优化算法(牛顿法、梯度下降法、最速下降法)进行了介绍和比较,并结合算法的数学原理和实际案例给出了优化算法选择的一些建议。
阅读本文的基础准备
线性代数
多变量微积分
对凸函数的基本知识
我们都知道,机器学习中最重要的内容之一就是优化问题。因此,找到一个能够对函数做合理优化的算法始终是我们关注的问题。当前,我们使用最多的优化算法之一是梯度下降算法。在本文中,我们会对梯度下降算法以及一些其他的优化算法进行介绍,并尝试从理论角度来理解它们。本文介绍的核心算法包括:
牛顿法(Newton’s Method)
最速下降法(Steep Descent)
梯度下降法(Gradient Descent)
如果想对这些算法有更多了解,你可以阅读斯坦福大学的《凸函数优化—:第三部分》教材。在本文中,我们主要关注二次函数和多项式函数。
对待优化函数的基本假设
一般而言,我们假设我们处理的函数的导数都是连续的(例如,f ∈ C¹)。对于牛顿法,我们还需要假设函数的二阶导数也是连续的(例如, f ∈ C²)。最后,我们还需要假设需要最小化的函数是凸函数。这样一来,如果我们的算法集中到一个点(一般称为局部最小值),我们就可以保证这个值是一个全局最优。
牛顿法
单变量函数的情况
x_n = starting pointx_n1 = x_n - (f'(x_n)/f''(x_n))while (f(x_n) != f(x_n1)): x_n = x_n1 x_n1 = x_n - (f'(x_n)/f''(x_n))
牛顿法的基本思想是,需要优化的函数f在局部可以近似表示为一个二次函数。我们只需要找到这个二次函数的最小值,并将该点的x值记录下来。之后重复这一步骤,直到最小值不再变化为止。
多变量函数的情况
对于单变量的情况,牛顿法比较可靠。但是在实际问题中,我们处理的单变量情形其实很少。大多数时候,我们需要优化的函数都包含很多变量(例如,定义在实数集ℝn的函数)。因此,这里我们需要对多变量的情形进行讨论。
假设x∈ ℝn,则有:
x_n = starting_pointx_n1 = x_n - inverse(hessian_matrix) (gradient(x_n))while (f(x_n) != f(x_n1)):x_n = x_n1 x_n1 = x_n - inverse(hessian_matrix) (gradient(x_n))
其中,gradient(x_n)是函数位于x_n点时的梯度向量,hessian_matrix是一个尺寸为 nxn 的黑塞矩阵(hessian matrix),其值是函数位于x_n的二阶导数。我们都知道,矩阵转换的算法复杂度是非常高的(O(n³)),因此牛顿法在这种情形下并不常用。
梯度下降
梯度下降是目前为止在机器学习和其他优化问题中使用的最多的优化算法。梯度算法的基本思想是,在每次迭代中向梯度方向走一小步。梯度算法还涉及一个恒定的alpha变量,该变量规定每次跨步的步长。下面是算法示例:
alpha = small_constantx_n = starting_pointx_n1 = x_n - alpha * gradient(x_n)while (f(x_n) != f(x_n1)): # May take a long time to converge x_n = x_n1 x_n1 = x_n - alpha * gradient(x_n)
这里,alpha是在每次迭代中更新x_n时都需要使用的变量(一般称为超参数)。下面我们对alpha值的选择进行简单分析。
如果我们选择一个很大的alpha,我们很可能会越过最优点,并离最优点越来越远。事实上,如果alpha的值过大,我们甚至会完全偏离最优点。

当alpha的值过大时,10次迭代后的梯度下降情况
另外,如果我们选择的alpha值过小,则可能需要经过非常多次迭代才能找到最优值。并且,当我们接近最优值时,梯度会接近于0。因此 ,如果alpha的值过小,我们有可能永远都无法到达最优点。

当alpha的值过小时,10次迭代后的梯度下降情况
因此,我们可能需要多尝试一些alpha的值,才能找到最优的选择。如果选择了一个合适的alpha值,我们在迭代时往往能节省很多时间。
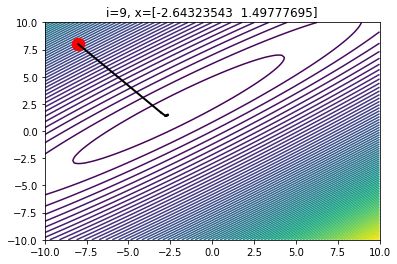
当alpha的值合理时,10次迭代后的梯度下降情况
最速下降法
最速下降法和梯度下降法非常相似,但是最速下降法对每次迭代时要求步长的值为最优。下面是最速下降法的算法示例:
x_n = starting_pointalpha_k = get_optimizer(f(x_n - alpha * gradient(x_n)))x_n1 = x_n - alpha_n * gradient(x_n)while (f(x_n) != f(x_n1)): x_n = x_n1 alpha_k = get_optimizer(f(x_n - alpha * gradient(x_n))) x_n1 = x_n - alpha_n * gradient(x_n)
其中,x_n和x_n1是ℝn上的向量,是算法的输入,gradient是函数 f 在点x_n的梯度,alpha_k的数学表示如下:

因此,在对原始函数进行优化时,我们需要在每一次迭代中对一个内部函数进行优化。这样做的优点是,这个内部优化函数是一个单变量函数,它的优化不会非常复杂(例如,我们可以使用牛顿法来作为这里的函数)。但是在更多情形下,在每一步中优化这个函数都会带来比较昂贵的花销。
二次式函数的特殊情形
对于均方误差函数:

其中,I 是单位矩阵,y=Qw + b 。为了简化讨论,这里我们只考虑寻找权重w最优值的情形(假设b是连续的)。将等式y=Qw + b带入上式并进行一定整理后,我们可以得到如下等式:

现在我们重新查看一下g(α), 我们会发现,如果我们使用点 αk 处的梯度,由于其为最优值,该梯度应当为0。因此我们有如下等式:

对上式进行简化,并将 f 的梯度带入后,我们可以得到对于 αk 的表示如下:

这就是在二次函数情形下 αk 的值。
对二次函数的收敛性分析
对于定义在ℝ²上的二次函数,最速下降法一般用来在非常接近最优值时使用,使用步数不超过十步。

二维中的最速下降在4次迭代后的情形
在上图中,每一次迭代中的改变方向都是垂直的。在3到4次迭代后,我们可以发现导数的变化基本可以忽略不计了。
为什么最速下降法应用很少?
最速下降法算法远远满足了超参数调优的需求,并且保证能找到局部最小值。但是为什么该算法应用不多呢?最速下降法的问题在于,每一步都需要对 aplha_k 进行优化,这样做的成本相对高昂。
例如,对于二次函数,每次迭代都需要计算多次矩阵乘法以及向量点乘。但对于梯度下降,每一步只需要计算导数并更新值就可以了,这样做的成本远远低于最速下降算法。
最速下降算法的另一个问题是对于非凸函数的优化存在困难。对于非凸函数,aplha_k 可能没有固定的值。
对于梯度下降法和最速下降法的对比
在这一部分,我们对梯度下降法和最速下降法进行对比,并比较它们在时间代价上的差异。首先,我们对比了两种算法的时间花销。我们会创建一个二次函数:f:ℝ²⁰⁰⁰→ℝ (该函数为一个2000x2000的矩阵)。我们将对该函数进行优化,并限制迭代次数为1000次。之后,我们会对两种算法的时间花销进行对比,并查看 x_n 值与最优点的距离。
我们先来看一下最速下降法:
0 Diff: 117727672.56583363 alpha value: 8.032725864804974e-06 100 Diff: 9264.791000127792 alpha value: 1.0176428564615889e-05 200 Diff: 1641.154644548893 alpha value: 1.0236993350903281e-05 300 Diff: 590.5089467763901 alpha value: 1.0254560482036439e-05 400 Diff: 279.2355946302414 alpha value: 1.0263893422517941e-05 500 Diff: 155.43169915676117 alpha value: 1.0270028681773919e-05 600 Diff: 96.61812579631805 alpha value: 1.0274280663010468e-05 700 Diff: 64.87719237804413 alpha value: 1.027728512597358e-05 800 Diff: 46.03102707862854 alpha value: 1.0279461929697766e-05 900 Diff: 34.00975978374481 alpha value: 1.0281092917213468e-05 Optimizer found with x = [-1.68825261 5.31853629 -3.45322318 ... 1.59365232 -2.85114689 5.04026352] and f(x)=-511573479.5792374 in 1000 iterationsTotal time taken: 1min 28s
下面是梯度下降法的情况,其中 alpha = 0.000001:
0 Diff: 26206321.312622845 alpha value: 1e-06 100 Diff: 112613.38076114655 alpha value: 1e-06 200 Diff: 21639.659786581993 alpha value: 1e-06 300 Diff: 7891.810685873032 alpha value: 1e-06 400 Diff: 3793.90934664011 alpha value: 1e-06 500 Diff: 2143.767760157585 alpha value: 1e-06 600 Diff: 1348.4947955012321 alpha value: 1e-06 700 Diff: 914.9099299907684 alpha value: 1e-06 800 Diff: 655.9336211681366 alpha value: 1e-06 900 Diff: 490.05882585048676 alpha value: 1e-06 Optimizer found with x = [-1.80862488 4.66644055 -3.08228401 ... 2.46891076 -2.57581774 5.34672724] and f(x)=-511336392.26658595 in 1000 iterationsTotal time taken: 1min 16s
我们可以发现,梯度下降法的速度比最速下降法略快(几秒或几分钟)。但更重要的是,最速下降法采取的步长比梯度下降法更加合理,尽管梯度下降法的α的值并非最优。在上述示例中, 对于梯度下降算法,f(xprex) 和 f(curr)在第900次迭代时的差为450。而最速下降法在很多次迭代前就已经达到这个值了(大约在第300次到第400次迭代之间)。
因此,我们尝试限制最速下降法的迭代次数为300,输出如下:
0 Diff: 118618752.30065191 alpha value: 8.569151292666038e-06 100 Diff: 8281.239207088947 alpha value: 1.1021416896567156e-05 200 Diff: 1463.1741587519646 alpha value: 1.1087402059869253e-05 300 Diff: 526.3014997839928 alpha value: 1.1106776689082503e-05 Optimizer found with x = [-1.33362899 5.89337889 -3.31827817 ... 1.77032789 -2.86779156 4.56444743] and f(x)=-511526291.3367646 in 400 iterationsTime taken: 35.8s
可以发现,最速下降法的速度实际更快。在此情形中,我们在每次迭代使用更少的步数就能逼近最优值。事实上,如果你的目标是估计最优值,最速下降法会比梯度下降法更合适。对于低维度的函数,10步的最速下降法就会比经过1000次迭代的梯度下降法更接近最优值。
下面这个例子中,我们使用了一个定义在 ℝ³⁰→ℝ 上的二次函数。10步后,最速下降法的得到函数值为 f(x) = -62434.18。而梯度下降法在1000步后得到的函数值为 f(x) = -61596.84。可以发现,最速下降法在10步后的结果就优于梯度下降法在1000步后的结果。
需要记住的是,这种情形仅在处理二次函数的时候适用。整体而言,在每次迭代中都找到 αk的最优值是较为困难的。对函数 g(α) 求最优值并不总能得到 αk 的最优值。通常,我们会使用迭代的算法来对优化函数求最小值。在这种情形下,最速下降法与梯度下降法相比就比较慢了。因此,最速下降法在实际应用中并不常见。
总结
在本文中,我们学习了三种下降算法:
牛顿法(Newton's method)
牛顿法提供了对函数的二阶近似,并在每一步都对函数进行优化。其最大的问题在于,在优化过程中需要进行矩阵转换,对于多变量情形花销过高(尤其是向量的特征较多的时候)。
梯度下降(Gradient Descent)
梯度下降是最常用的优化算法。由于该算法在每步只对导数进行计算,其花销较低,速度更快。但是在使用该算法时,需要对步长的超参数进行多次的猜测和尝试。
最速下降法(Steepest Descent)
最速下降法在每步都对函数的梯度向量寻找最优步长。它的问题在于,在每次迭代中需要对相关的函数进行优化,这会带来很多花销。对于二次函数的情形,尽管每步都涉及很多矩阵运算,最速下降法的效果仍然更优。
-
机器学习算法的5种基本算子2023-08-17 2643
-
基于机器学习算法的校准优化方案2023-06-29 820
-
机器学习之关联分析介绍2023-03-25 2634
-
常用机器学习算法的基本概念和特点2023-01-17 4528
-
机器学习算法的基础介绍2022-10-24 2585
-
算法的三种结构介绍2021-11-08 1359
-
10大常用机器学习算法汇总2020-11-20 3159
-
深度学习的三种学习模式介绍2020-10-23 13673
-
介绍机器学习中常用的三种优化算法2020-05-04 3831
-
机器学习新手必学的三种优化算法(牛顿法、梯度下降法、最速下降法)2019-05-07 5859
-
机器学习算法常用指标汇总2019-02-13 5831
-
NLP的介绍和如何利用机器学习进行NLP以及三种NLP技术的详细介绍2018-06-10 78601
-
机器学习经典算法-最优化方法2017-09-04 835
-
数控机床插补算法中最常用的三种算法源码2016-11-08 2026
全部0条评论

快来发表一下你的评论吧 !

