以太坊中运用最多的三种树结构介绍

树这种数据结构，在区块链中扮演着重要的角色，交易的数据，账号的管理，交易的收据信息等都是一树为基础。本文主要介绍三种树，也是在以太坊的中运用最多的三种树结构：Trie树， Patricia Trie和Merkle树。

Trie树

Trie树，又称字典树，单词查找树或者前缀树，是一种用于快速检索的多叉树结构，如英文字母的字典树是一个26叉树，数字的字典树是一个10叉树。举个例子，用trie树保存10个节点的6个字符串：tea，ten，to，in，inn，int。具体图如下：

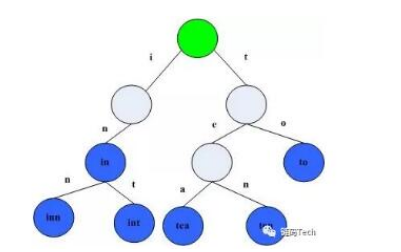
可以看到字符串in，inn和int的公共前缀是“in”，这样的效果就是压缩了数据，减少空间的存储。那么如果没有公共的前缀，那么问题就来了，占用大量的空间，这样的检索的速度将会减慢。

· Patricia Trie树

Patricia Trie树的不同之处在于Trie树给每一个字符串分配一个节点，这样将使那些很长但又没有公共节点的字符串的Trie树退化成数组。在以太坊里面会由黑客构造很多这种节点造成拒绝服务攻击。前缀树的不同之处在于如果节点公共前缀，那么就使用公共前缀，否则就把剩下的所有节点插入同一个节点。Patricia相对Tire的优化正如下图：

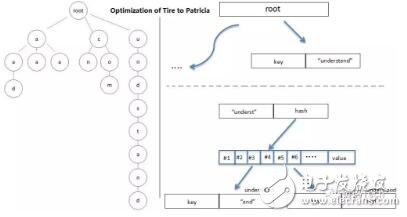
我们可以举个例子来总结Patricia Trie树，如下图：

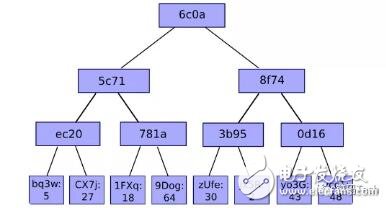
最终的8个key对应的Value 如下表：

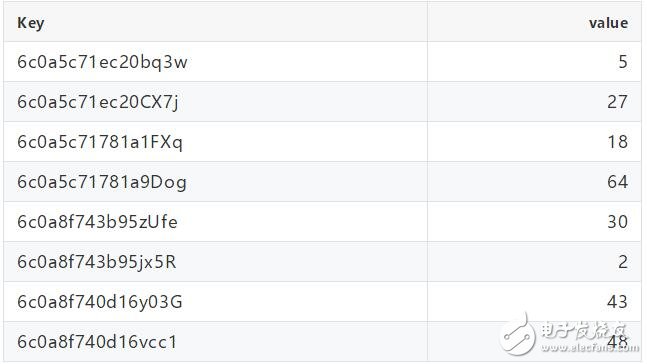
· Merkle Tree

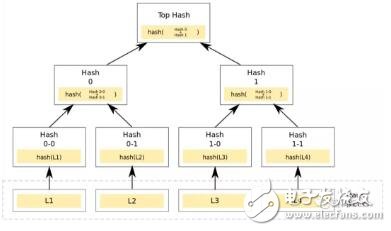
称作Hash Tree，顾名思义，就是存储hash值的一棵树。Merkle树的叶子是数据块（例如，文件或者文件的集合）的hash值。非叶节点是其对应子节点串联字符串的hash。这个树结构是比特币采用的数据结构。Merkle Tree的主要作用是当我拿到Top Hash的时候，这个hash值代表了整颗树的信息摘要，当树里面任何一个数据发生了变动，都会导致Top Hash的值发生变化。而Top Hash的值是会存储到区块链的区块头里面去的， 区块头是必须经过工作量证明。这也就是说我只要拿到一个区块头，就可以对区块信息进行验证。

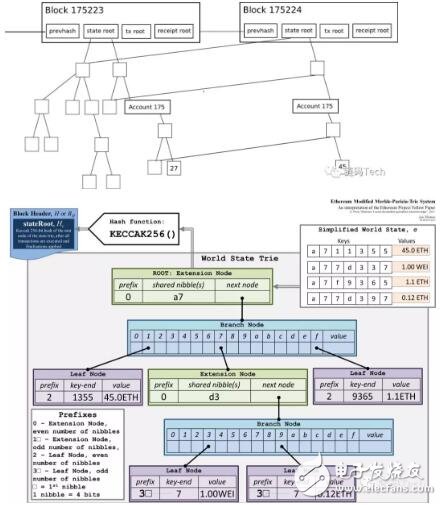
· ETH Merkle Patricia Tries 树

以太坊的每个区块头包含三个重要的树：

1.交易树

2.收据树（交易执行过程中的一些数据）

3.状态树（账号信息， 合约账户和用户账户）

如下通过例子来介绍，例如，两个区块头，其中state root，tx root receipt root分别存储了这三棵树的树根，第二个区块显示了当账号 175的数据变更（27 -》 45）的时候，只需要存储跟这个账号相关的部分数据，而且老的区块中的数据还是可以正常访问。如下图：

· 算法解释

假设输入值J，包含Key Value对的集合（Key Value都是字节数组）：

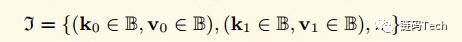
当使用这个集合的时候，我们将集合表示如下：

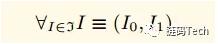
对应特定字节，我们表示为对应的半字节（nibble），其中Y集合在Hex-Prefix Encoding中有说明，意为半字节（4bit）集合（之所以采用半字节，其与后续说明的分支节点branch node结构以及key中编码flag有关），公式如下：

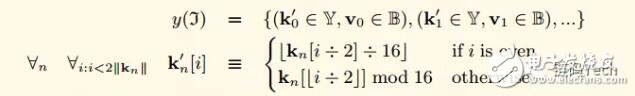
在Tries树中有三种节点：

1.叶子节点（Leaf）： 叶子节点包含两个字段， 第一个字段是剩下的Key的半字节编码，而且半字节编码方法的第二个参数为true， 第二个字段是Value

2.扩展节点（Extention）： 扩展节点也包含两个字段， 第一个字段是剩下的Key的可以至少被两个剩下节点共享的部分的半字节编码，第二个字段是n（J，j）

3.分支节点（Branch）： 分支节点包含了17个字段，其前16个项目对应于这些点在其遍历中的键的十六个可能的半字节值中的每一个。第17个字段是存储那些在当前结点结束了的节点（例如， 有三个key，分别是 （abc ，abd， ab） 第17个字段储存了ab节点的值）

分支节点只有在需要的时候使用， 对于一个只有一个非空 key value对的Trie树，可能不存在分支节点。如果使用公式来定义这三种节点， 那么公式如下：图中的HP函数代表Hex-Prefix Encoding，是一种半字节编码格式，RLP是使用RLP进行序列化的函数。

如果当前需要编码的KV集合只剩下一条数据，那么这条数据按照第一条规则进行编码。

如果当前需要编码的KV集合有公共前缀，那么提取最大公共前缀并使用第二条规则进行处理。

如果不是上面两种情况，那么使用分支节点进行集合切分，因为key是使用HP进行编码的，所以可能的分支只有0-15这16个分支。可以看到u的值由n进行递归定义，而如果有节点刚好在这里完结了，那么第17个元素v就是为这种情况准备的。

对于数据应该如何存储和不应该如何存储， 黄皮书中说明没有显示的定义。所以这是一个实现上的问题。我们简单的定义了一个函数来把J映射为一个Hash。 我们认为对于任意一个J，只存在唯一一个Hash值。