奇异值分解和矩阵分解傻傻分不清楚？一文帮你理清两者差异！

在推荐系统的相关研究中，我们常常用到两个相关概念：矩阵分解和奇异值分解。这两个概念是同一种算法吗？两者到底有什么差别？在本文中，作者梳理了两种算法的概念、来源和内容，并进行了比较。通过对相关内容的梳理，作者提出，矩阵分解是推荐系统中最初使用的概念，奇异值分解是对该方法的进一步发展。在现在的讨论中，一般将两种方法统一成为奇异值分解。

在 Andrew Ng 教授的机器学习课程中，介绍推荐系统时经常涉及矩阵分解、奇异值分解等数学知识，这些概念并不是很好理解。在 Andrew Ng 教授的课程提到了一种称为称为 (低因子) 矩阵分解的方法，而在 Google 搜索会得到另一个名称：奇异值分解。网络资源中对于该算法的解释和 Andrew Ng 教授存在差异，但很多人都认为这两个名称指的是同一种算法。为了更好的梳理这两个概念，在本文中，我对两者进行了分别介绍，并对比了它们的不同。

推荐系统

推荐系统 (Recommender Systems， RS) 是一种自动化的针对用户的内容推荐方式，被广泛用于电子商务公司，流媒体服务 (streaming services) 和新闻网站等系统。根据用户的喜好，推荐系统能够投其所好，为用户推荐一些合适的内容，以便减少用户筛选过程中一些不必要的麻烦。

推荐系统并不是一种全新的技术，相关概念最晚在1990年就出现了。事实上，当前的机器学习热潮，一部分要归因于人们对 RS 的广泛关注。 在2006年，Netflix 赞助了一场为电影寻找最佳推荐系统的竞赛，在当时引起了一片轰动，也让推荐系统再次得到了广泛的关注。

矩阵表示

我们可以有很多种方式来向别人推荐一部电影。其中一种效果较好的策略，是将用户对电影的评分看做一个用户 x 电影矩阵，如下所示：

     

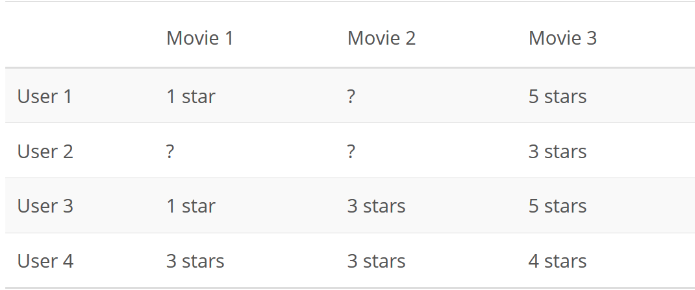
在该矩阵中，问号代表用户未评分的电影。随后，只需要以某种方式预测来用户对电影评分，并向用户推荐他们可能喜欢的电影。

矩阵分解

在 Netflix 举办的比赛上，参赛者 Simon Funk 提出了一个很好的想法，即用户对电影的评分不是随给出的。用户会基于一定的逻辑，针对电影中他所所喜欢的部分 (如特定的女演员或类型) 和不喜欢的情节 (长时间或糟糕的笑话) 赋予不同的权重，并进行加权计算，最后得到一个分数作为该电影的评分。这个过程可以用如下公式表示：

     

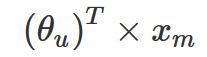
其中 xm 是电影 m 特征值的一个列向量，而 θᵤ 是另一个列向量，表示用户 u 赋予每个电影特征的权重。每个用户都有不同的权重集合，而每个电影的特征也对应不同的特征集合。

事实证明，如果能够任意地修改特征的数量并忽略所缺失的那部分电影评分，那么就可以找到一组权重和特征值，依据这些值所创建新矩阵与原始的评分矩阵是很接近的。这一过程可以通过梯度下降来实现，且类似于线性回归中所使用的梯度下降，只不过我们需要同时优化权重和特征这两组参数。以上文提供的用户-电影矩阵为例，优化后得到的结果将生成如下新的矩阵：

       

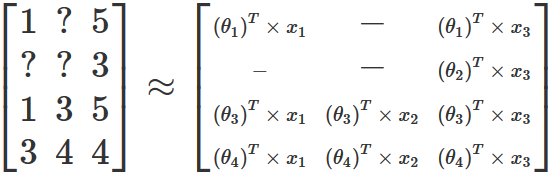
值得注意的是，在大多数真实数据集中，生成的结果矩阵并不会精确地与原始矩阵保持一致。因为在现实生活中，用户不会对通过矩阵乘法和求和等操作对电影进行评分。大多数情况下，用户对电影进行评分只是一种主观性的行为，且可能受到各种外部因素的影响。尽管如此，这里所介绍的方法还是希望通过数学公式来表达用户在电影评分时的主要逻辑。

通过上面的计算，现在我们已经得到了一个近似矩阵，那该如何来预测缺失的电影评级呢？通过回顾上面的计算过程，我们可以发现，为了构建这个新矩阵，这里定义了一个公式来填充矩阵中的所有值，包括原始矩阵中的缺失值。因此，如果想要预测缺失的用户电影评分，这里只需获取该缺失电影的所有特征值，再乘以该用户的所有权重并将所有内容相加，就能得到用户对该电影的评分。因此在这里，如果想要预测用户2对电影1的评级，可以通过以下计算：

     

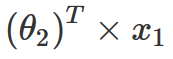
为了简化表达式，在这里可以对 θ 和 x 进行分离，并将它们放入各自的矩阵(比如 P 和 Q)。

以上就是 Funk 所提出的矩阵分解方法，也是 Andrew Ng 教授在课上所提到的矩阵分解。该方法在当时 Netflix 竞赛中获得第三名，引起了广泛的关注，并在当前许多应用中仍被使用。

奇异值分解

下面介绍奇异值分解 (Singular Value Decomposition, SVD)。SVD 方法是将一个矩阵分解为三个矩阵的矩阵分解方法，即 A =UΣVᵀ，且三个分解矩阵会具有一些较好的数学特性。

SVD 方法具有广泛的应用，其中之一就是主成分分析（Principal Component Analysis, PCA） ，该方法能够将维度 n 的数据集减少到 k 个维度 (k

这里不再展开介绍 SVD 方法的详细信息。我们只需要记住，奇异值分解与矩阵分解的处理方式不同。使用SVD 方法会得到三个分解矩阵，而 Funk 提出的矩阵分解方式只创建了两个矩阵。

那为什么在每次搜索推荐系统时总会弹出 SVD 的相关内容呢？ Luis Argerich 认为原因在于：

       

事实上，矩阵分解是推荐系统中首先使用的方法，而 SVD++ 可视为是对它的一种扩展形式。正如 Xavier Amatriain 所说的那样：

     

而 Wikipedia 在对矩阵分解（推荐系统）的相关条目中也有类似的表述：

       

最后，简单进行一下总结：

奇异值分解（SVD）是一种相对复杂的数学技术，它将矩阵分解为三个新的矩阵，并广泛应用于当前许多的应用中，包括主成分分析（PCA）和推荐系统（RS）。

Simon Funk 在2006年的 Netflix 竞赛中提出并使用了一个非常好的策略，改方法将矩阵分解为两个权重矩阵，并使用梯度下降来找到特征和权重所对应的的最优值。实质上，这是不同于 SVD 方法的另一种技术，将其称为矩阵分解更为合适。

随着这两种方法的广泛应用，研究者并没有严谨地在术语上区分这两种方法，而是统一将其称为 SVD。