三种常见的损失函数和两种常用的激活函数介绍和可视化

【导语】本文对梯度函数和损失函数间的关系进行了介绍，并通过可视化方式进行了详细展示。另外，作者对三种常见的损失函数和两种常用的激活函数也进行了介绍和可视化。

你需要掌握关于神经网络训练的基础知识。本文尝试通过可视化方法，对损失函数、梯度下降和反向传播之间的关系进行介绍。

损失函数和梯度下降之间的关系

为了对梯度下降过程进行可视化，我们先来看一个简单的情况：假设神经网络的最后一个节点输出一个权重数w，该网络的目标值是0。在这种情况下，网络所使用的损失函数为均方误差（MSE）。

当w大于0时，MSE的导数 dy/dw 值为正。dy/dw 为正的原因可以解释为，w中的正方向变化将导致y的正方向变化。为了减少损失值，需要在w的负方向上进行如下变换：

当w小于0时，MSE的导数 dy/dw 值为负，这意味着w中的正方向变化将导致y的负方向变化。 为了减少损失，需要在w的正方向上做如下变换：

因此，权重更新的公式如下：

其中 learning_rate 是一个常量，用于调节每次更新的导数的百分比。调整 Learning_rate 值主要是用于防止w更新步伐太小或太大，或者避免梯度爆炸（梯度太大）或梯度消失的问题（梯度太小）。

下图展示了一个更长且更贴近实际的计算过程，在该计算过程中，需要使用sigmoid激活函数对权重进行处理。为了更新权重w1，相对于w1的损失函数的导数可以以如下的方式得到：

损失函数对权重的求导过程

从上面阐释的步骤可以看出，神经网络中的权重由损失函数的导数而不是损失函数本身来进行更新或反向传播。因此，损失函数本身对反向传播并没有影响。下面对各类损失函数进行了展示：

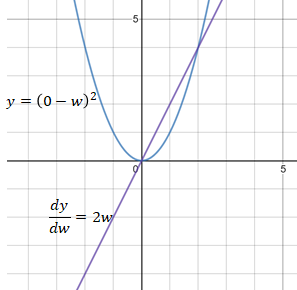
L2损失函数

MSE（L2损失）的导数更新的步长幅度为2w。 当w远离目标值0时，MSE导数的步长幅度变化有助于向w反向传播更大的步长，当w更接近目标值0时，该变化使得向w进行反向传播的步长变小。

L1损失函数

MAE（L1损失）的导数是值为1或负1的常数，这可能不是理想的区分w与目标值之间距离的方式。

交叉熵损失函数

交叉熵损失函数中w的范围是0和1之间。当w接近1时，交叉熵减少到0。交叉熵的导数是 -1/w。

Sigmoid激活函数

Sigmoid函数的导数值域范围在0到0.25之间。 sigmoid函数导数的多个乘积可能会得到一个接近于0的非常小的数字，这会使反向传播失效。这类问题常被称为梯度消失。

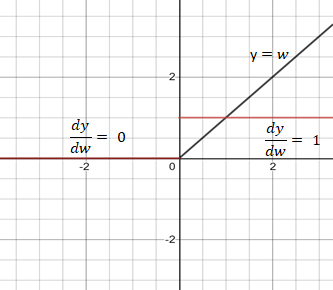
Relu激活函数

Relu是一个较好的激活函数，其导数为1或0，在反向传播中使网络持续更新权重或不对权重进行更新。