星系共识的随机数生成算法对共识协议的作用

一、随机数对于区块链系统的重要作用

在正式谈随机数的作用之前，我们需要了解一个概念，那就是“熵”（entropy）。熵对于物理学领域的朋友一定不会陌生，它是体系混乱程度的度量。在1948年，香农（Claude Elwood Shannon）提出了信息熵的概念，去描述信源的不确信度。简而言之，熵就是不确定性的度量。举一个简单的例子：“北京明天的天气状况”，可能是晴天，也可能是阴天或者下雨，结果是不确定的，因此熵为正数；“地球明天要毁灭”，我们知道地球明天不会毁灭，这是确定的结果，因此熵为零。

那么熵和区块链系统有何关系呢？可以说，熵对于区块链系统是至关重要的，是整个系统运行的安全保障。以比特币系统为例，它采取PoW作为共识算法，矿工进行大量哈希计算去争夺出块权，任何高度区块的出块者身份都无法提前预测，这就是熵在比特币系统中的体现。试想如果熵为0，即每个区块的出块者都是事先确定的或者人为可控，那么必然会出现合谋、分叉等攻击。因此任何区块链系统都需要一种安全有效的方式为系统引入熵。基于PoW共识的区块链系统由于挖矿的随机性，以天然的方式为系统引入了熵，然而对于PoS和DPoS共识的区块链系统，就需要单独设计一种方式去引入熵，那就是随机数生成算法。可以说随机数生成算法是设计共识机制的主要挑战之一，也是衡量共识机制优劣的重要标准之一。

二、随机数生成算法优劣的衡量标准

既然随机数生成算法这么重要，那么一个好的随机数生成算法应该是什么样子呢？从安全和实用角度而言，它应当满足以下六大性质：

1. 去中心化（Distributed）：随机数的生成过程要是去中心化的，不能依赖或者借助可信第三方完成。

2. 不可预测（Unpredictable）：根据历史产生的随机数或其他信息无法预测未来的随机数，这是“随机”的基本要求。

3. 无偏性（Unbiased）：任何人都无法通过计算能力或者后发优势去针对性左右随机数的生成结果。

4. 均匀分布（Uniformity）：输出的随机数在其值域内是均匀分布的。

5. 保证输出（Guaranteed Output Delivery）：随机数生成算法的参与者无法通过违背算法的方式使得无法输出随机数，即必然会有随机数输出。

6. 公开可验证（Publicly Verifiable）：没参与随机数生成的节点可以以后验的方式，监督协议的执行，验证随机数是可信和无偏的。

以上六大性质对于随机数生成算法至关重要，违背其中任意一条都可能会导致严重的安全漏洞。据区块链安全公司PeckShield披露，EOS上有超过8个竞猜项目遭受黑客攻击并获利几百万美元，严重威胁到了EOS正常生态秩序，而大部分攻击成功的原因都与随机数生成漏洞有关。我们以EOS.WIN项目为例，剖析其随机数算法漏洞根源。

EOS.WIN支持的一个游戏是猜数字，即用户输入某个数字并压大或者压小，然后系统随机生成一个数字，如果用户压对大小，则视为中奖并获取收益。显然如果能够控制系统随机生成的数字，就可以左右游戏的结果。而决定EOS.WIN系统随机数生成的因素为交易哈希ID、成交区块高度、成交区块前缀、全局开奖序号等。其中成交区块高度、成交区块前缀虽然是未来某区块信息，但是在实施过程系统指定使用当前同步到的最新块信息，因而是确定的；同时，交易哈希ID能够通过交易内action结合块信息预先计算。于是随机数的生成仅依赖于全局开奖序号了。攻击者利用不断制造错误交易，造成交易状态回滚，控制全局开奖序号，从而控制随机数的生成，直到中奖。显而易见，EOS.WIN的随机数生成算法不满足上述的第二条性质（不可预测性）和第三条性质（无偏性），因此存在漏洞，最终被攻击者有效攻击。

三、星系共识随机数生成算法

星系共识中的RNP星群借助承诺、零知识证明、门限秘密分享、门限签名、椭圆曲线序对等多种密码学手段，实现了安全高效的随机数生成算法，为整个共识过程安全提供了数据基础。为了能够形象介绍随机数生成算法的设计初衷以及其精妙之处，我们将其类比一个简单的游戏：

纸牌游戏

Alice和Bob玩纸牌游戏，两人分别秘密选一张扑克牌放在桌面下方，选定之后，同时将纸牌亮在桌面上。如果两张纸牌的点数和为偶数，则Alice获胜；否则，为Bob获胜。

这个游戏看似简单，但是在区块链上公平的进行并不容易，要通过多种手段防止Alice或者Bob作弊。我们接下来一步一步分析：

问题1：Alice和Bob选定之后就不能再更换扑克牌，否则就可以根据对方扑克牌的点数决定自己扑克牌点数，从而获取胜利。例如，Alice如果可以更换扑克牌，那么只要保证自己所选扑克牌和Bob的扑克牌点数具有相同奇偶性，那么点数和总为偶数，Alice便可以获胜。

星系共识通过使用“承诺”（Commitment，在配图中用CM指代Commitment）的方式来保证不会发生以上作弊行为。“承诺”是一种密码学工具，能够保证在不暴露原始数据的基础上，将其进行“证据留存”，它和明文是一一对应的，任何人都可以验证二者的对应关系是否成立。

结合我们的例子形象理解就是，Alice和Bob将自己选定扑克牌撕一个小角下来，放在桌面上，这个小角不会暴露扑克的点数，而且只与撕坏的另一部分才能够拼接为一张完整的扑克牌。在星系共识协议中，这是Random Beacon的DKG1（Decentralized Key Generation）阶段，每个RNP（Random Number Proposer）节点计算其所选数据的承诺并发送到链上进行存证。

问题2：Alice和Bob在选好扑克牌之后，在正式亮牌之前要对自己的扑克牌保密，不能让对方看到。同时在亮牌时候要证明这张牌确实是之前选定的牌，而不是新选的另一张牌。

星系共识通过公钥加密算法加密原始数据，之后将加密结果发送到链上，保证了数据的机密性；同时使用零知识证明保证上链的加密数据与承诺完全匹配。结合我们的例子形象理解就是，Alice和Bob将被撕过角的牌从桌下取出，扣在桌面上，并且二者都验证扣在桌面上的牌与之前放在桌上的小角能够拼接为一张完整的纸牌。在星系共识协议中，这是Random Beacon的DKG2阶段，每个RNP节点将其给其他节点的数据通过对方公钥加密之后发送到链上（下图中S1，S2，Sn为经公钥加密后的链上数据），同时发送到链上的还有DLEQ-Proof（非交互零知识证明），用于证明加密内容与承诺CM是匹配的。这个阶段之后，所有节点都可以从链上获取其他节点发送的数据，并且在本地解密为明文。

问题3：开牌之后，需要计算两张扑克牌的点数。我们要保证Alice和Bob都要计算出同一正确结果。这个问题看似很荒唐，但是却非常重要。因为某位玩家可能会装疯卖傻，故意计算错数字，从而降低游戏进行的效率。

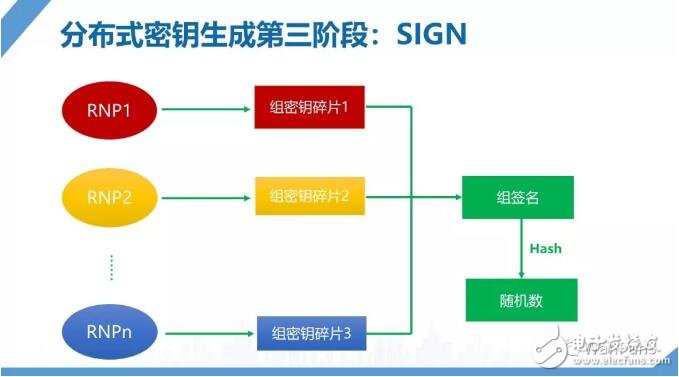
星系共识通过使用分布式密钥生成的算法解决了问题3，即所有RNP节点通过交互生成一个共同的组密钥（group secret key），这个密钥不会完整出现，而是分割为密钥碎片，每一个RNP节点掌握一个密钥碎片。之后，RNP节点能够合成组密钥签名，而签名的哈希值即为最终的随机数输出。由于组密钥是公共确定的，因此组密钥签名也是唯一固定的。结合我们的例子形象理解就是，Alice和Bob会计算得到共同的点数。

问题4：此时，无论是Alice还是Bob都不能够终止游戏的进行。也就是一旦游戏开始，就一定要正常结束，不能因为某一玩家拒绝配合游戏规则而导致游戏流产。

星系共识通过门限签名的方式解决了问题4，即只要超过门限值数量的RNP节点参与计算，就能够合成组密钥签名。个别RNP节点拒绝参与计算并不会影响结果的生成。结合我们的例子形象理解就是，即使Alice不想亮牌，Bob也有能力将两张牌亮出，从而完成游戏。

以上过程对应于星系共识协议中Random Beacon的SIGN阶段，在这一阶段中RNP节点合作生成组密钥签名并计算得到随机数输出。

现在我们把上述过程梳理一下：1. Alice和Bob扑克牌的点数之和是二者共同决定的；2. 每一局游戏的点数和都是独立的，不存在相互依赖的关系，因此历史游戏数据没有预测作用；3. Alice和Bob都无法提前知道对方的扑克牌点数，因此没有后发优势去左右点数之和；4. Alice和Bob可以选择任何一张扑克牌，因此点数分布是均匀的；5. Alice和Bob都无法中断游戏的进行；6. 任何第三方都可以对游戏过程进行审计，因为所有数据都在链上存证。

由以上分析可知，星系共识的随机数算法满足前文提到的六大性质，是安全高效的随机数生成算法。