ICLR 2019在官网公布了最佳论文奖！

ICLR 2019今天在官网公布了最佳论文奖！两篇最佳论文分别来自Mila/加拿大蒙特利尔大学、微软蒙特利尔研究院和MIT CSAIL，主题分别集中在NLP深度学习模型和神经网络压缩。

今天，ICLR 2019在官网公布了最佳论文奖！

两篇最佳论文分别来自Mila/加拿大蒙特利尔大学、微软蒙特利尔研究院和MIT CSAIL，主题分别集中在NLP深度学习模型和神经网络压缩。

ICLR 是深度学习领域的顶级会议，素有深度学习顶会 “无冕之王” 之称。今年的 ICLR 大会从5月6日到5月9日在美国新奥尔良市举行。

今年 ICLR 共接收 1578 篇投稿，相较去年 981 篇有了很大的增加，录用结果如下：1.5% 录用为 oral 论文（24 篇）、30.2% 录用为 poster 论文（476 篇)，58% 论文被拒（918 篇）、610% 撤回（160 篇）。

与往年一样，ICLR 2019采用公开评审制度，所有论文会匿名公开在 open review 网站上，接受同行们的匿名评分和提问。

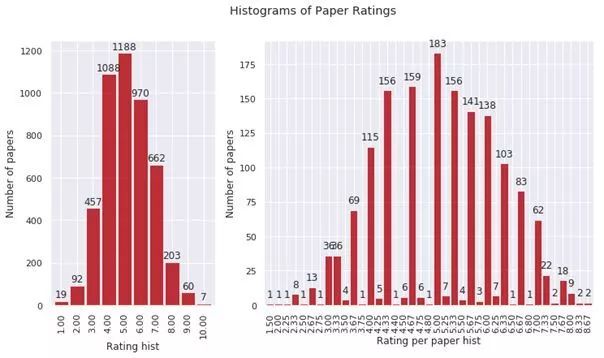
今年论文平均打分是 5.15

关键词排序前 50

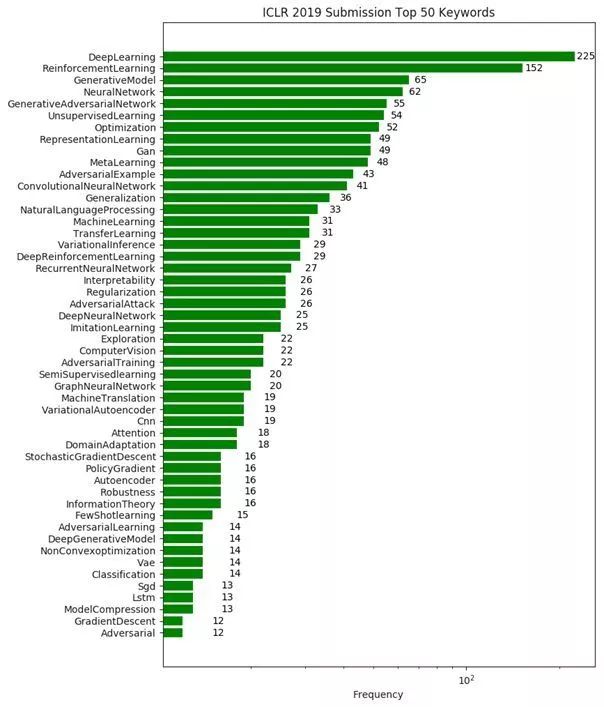
接下来，新智元带来两篇最佳论文的解读：

最佳论文1：有序神经元：将树结构集成到循环神经网络

标题：Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks 

《有序神经元：将树结构集成到循环神经网络》

作者：Yikang Shen, Shawn Tan, Alessandro Sordoni, Aaron Courville

作者机构：Mila/ 加拿大蒙特利尔大学、微软蒙特利尔研究院

论文地址：https://openreview.net/forum?id=B1l6qiR5F7

摘要：

自然语言是一种分层结构：较小的单元 (例如短语) 嵌套在较大的单元 (例如子句) 中。当较大的成分结束时，嵌套在其中的所有较小单元也必须结束。虽然标准的 LSTM 架构允许不同的神经元在不同的时间尺度上跟踪信息，但它并没有明确地偏向于对成分层次结构建模。

本文提出通过对神经元进行排序来增加这种归纳偏差 ; 一个主输入和遗忘门的向量确保当一个给定的神经元被更新时，按照顺序跟随它的所有神经元也被更新。所提出的新循环结构称为有序神经元 LSTM (ordered neurons LSTM, ON-LSTM)，在语言建模、无监督句法分析、目标语法评估和逻辑推理四个不同的任务上都取得了良好的性能。

关键词: 深度学习，自然语言处理，递归神经网络，语言建模

一句话概括：本文提出一种新的归纳偏置，将树结构集成到循环神经网络中。

从实用的角度看，将树结构集成到神经网络语言模型中有以下几个重要原因：

深度神经网络的一个关键特征是获得抽象层次不断增加的分层表示；

建模语言的组成效应，并为梯度反向传播提供快捷方式，以帮助解决长期依赖问题 ;

通过更好的归纳偏置改进泛化，同时能够减少对大量训练数据的需求。

图 1：由模型推断的二进制解析树 (左) 及其对应的 round-truth(右)。

问题是：具有对学习这种潜在树结构的归纳偏置的架构能否获得更好的语言模型 ?

在这篇论文中，我们提出有序神经元 (ordered neurons)，这是一种面向循环神经网络的新型归纳偏置。这种归纳偏置增强了存储在每个神经元中的信息的生命周期的分化：高级神经元存储长期信息，这些信息通过大量步骤保存，而低级神经元存储短期信息，这些信息可以很快被遗忘。

为了避免高级和低级神经元之间的固定划分，我们提出一种新的激活函数 ——cumulative softmax，或称为 cumax()，用于主动分配神经元来存储长 / 短期信息。

基于 cumax() 和 LSTM 架构，我们设计了一个新的模型 ON-LSTM，该模型偏向于执行类似树的组合操作。

ON-LSTM 模型在语言建模、无监督成分句法分析、目标句法评估和逻辑推理四项任务上都取得了良好的性能。对无监督成分句法分析的结果表明，所提出的归纳偏置比以前模型更符合人类专家提出的语法原则。实验还表明，在需要捕获长期依赖关系的任务中，ON-LSTM 模型的性能优于标准 LSTM 模型。

有序神经元

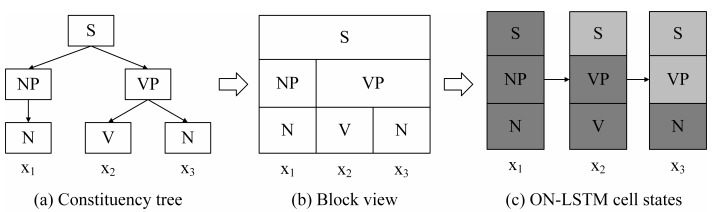
图 2：一个成分解析树和 ON-LSTM 的隐藏状态之间的对应关系

ON-LSTM

ON-LSTM 模型与标准 LSTM 的架构类似：

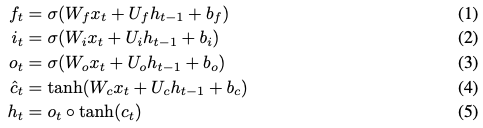
与 LSTM 的不同之处在于，这里用了一个新函数替换 cell state 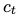的 update 函数。

实验

语言建模

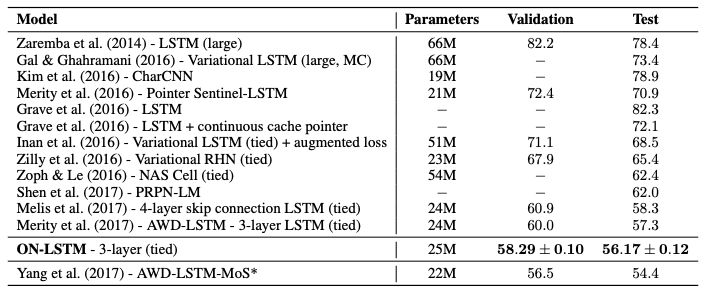
表 1：Penn Treebank 语言建模任务验证集和测试集上的单模型困惑度。

如表 1 所示，ON-LSTM 模型在共享相同的层数、嵌入维数和隐藏状态单元的情况下，比标准的 LSTM 性能更好。值得注意的是，我们可以在不添加 skip connection 或显著增加参数数量的情况下提高 LSTM 模型的性能。

无监督成分句法分析 (Constituency Parsing)

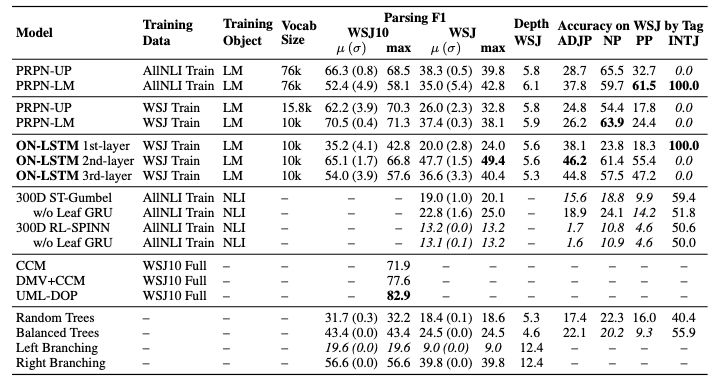
表 2：在 full WSJ10 和 WSJ test 两个数据集上评估的成分句法分析结果

目标句法评估

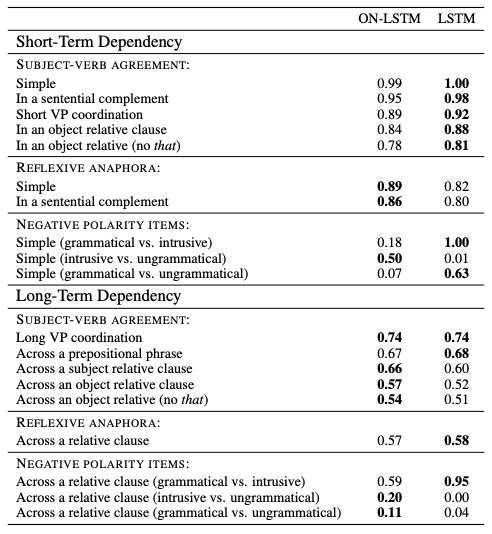
表 3：ON-LSTM 和 LSTM 在每个测试用例中的总体精度

表 3 显示，ON-LSTM 在长期依赖情况下表现更好，而基线 LSTM 在短期依赖情况下表现更好。不过，ON-LSTM 在验证集上实现了更好的困惑度。

逻辑推理

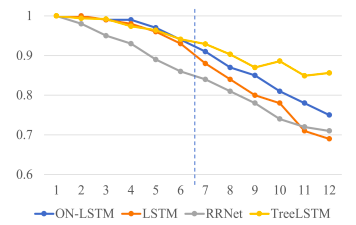
图 3：模型的测试准确性，在逻辑数据的短序列 (≤6) 上训练。

图 3 显示了 ON-LSTM 和标准 LSTM 在逻辑推理任务上的性能。

最佳论文2：彩票假设

标题：The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks 

《彩票假设：寻找稀疏的、可训练的神经网络》

作者：Jonathan Frankle, Michael Carbin

作者机构：MIT CSAIL

论文地址：https://openreview.net/forum?id=rJl-b3RcF7

摘要：

神经网络剪枝技术可以在不影响精度的前提下，将训练网络的参数数量减少 90% 以上，降低存储需求并提高推理的计算性能。然而，当前的经验是，剪枝产生的稀疏架构从一开始就很难训练，这同样可以提高训练性能。

我们发现，一种标准的剪枝技术可以自然地揭示子网络，这些子网络的初始化使它们能够有效地进行训练。基于这些结果，我们提出了 “彩票假设”(lottery ticket hypothesis)：包含子网络 (“中奖彩票”，winning tickets) 的密集、随机初始化的前馈网络，这些子网络在单独训练时，经过类似次数的迭代达到与原始网络相当的测试精度。我们找到的 “中奖彩票” 中了初始化彩票：它们的连接具有初始权重，这使得训练特别有效。

我们提出一个算法来确定中奖彩票，并激进型了一系列实验来支持彩票假说以及这些偶然初始化的重要性。我们发现，MNIST 和 CIFAR10 的中奖彩票的规模始终比几个全连接架构和卷积前馈架构小 10-20%。超过这个规模的话，我们发现中奖彩票比原来的网络学习速度更快，达到了更高的测试精度。

关键词：神经网络，稀疏性，剪枝，压缩，性能，架构搜索

一句话概括：可以在训练后剪枝权重的前馈神经网络，也可以在训练前剪枝相同的权重。

本文证明了，始终存在较小的子网络，它们从一开始就进行训练，学习速度至少与较大的子网络一样快，同时能达到类似的测试精度。

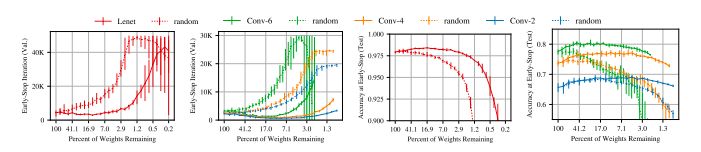
图 1：早期停止发生的迭代 (左边) 和用于 MNIST 的 Lenet 架构以及用于 CIFAR10 的conv2、conv4 和 conv6 架构的迭代 (右边) 的测试精度。虚线是随机抽样的稀疏网络。实线是中奖彩票。

图 1 中的实线显示了我们找到的网络，即 winning tickets。

论文提出了几个新概念，首先是 “彩票假设”(The Lottery Ticket Hypothesis)。

彩票假设：将一个复杂网络的所有参数当作一个奖池，奖池中存在一组子参数所对应的子网络（代表中奖号码，文中的 wining ticket），单独训练该子网络，可以达到原始网络的测试精度。

那么怎样找到中奖彩票呢？

确定中奖彩票：通过训练一个网络并修剪它的最小量级权重来确定中奖彩票。其余未修剪的连接构成了中奖彩票的架构。

具体来说，有以下 4 步：

随机初始化一个复杂神经网络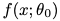

训练复杂网络 j 次，得到网络参数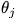

对模型按 p% 进行修剪，得到一个 mask m; 将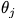

对留下来的模型，重新用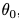

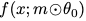
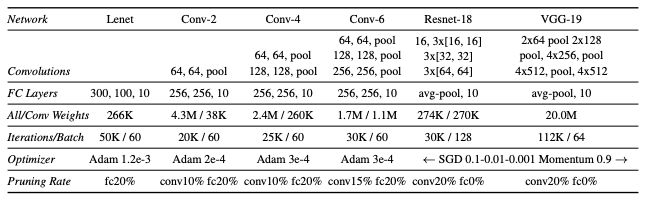
图 2：本文测试的架构

本文的贡献

我们证明剪枝可以揭示可训练的子网络，这些子网络达到了与原始网络相当的测试精度；

我们证明剪枝发现的中奖彩票比原始网络学习更快，同时具有更高的测试精度和更好的泛化能力。

我们提出 “彩票假设”，作为神经网络组成的新视角，可以解释这些发现。

应用

本文对彩票假设进行了实证研究。既然我们已经证明了中奖彩票的存在，我们希望利用这一知识：

提高训练性能。由于中奖彩票可以从一开始就单独进行训练，我们希望能够设计出能够搜索中奖彩票并尽早进行修剪的训练方案。

设计更好的网络。中奖彩票揭示了稀疏架构和特别擅长学习的初始化的组合。我们可以从中获得灵感，设计有助于学习的新架构和初始化方案。我们甚至可以把为一项任务发现的中奖彩票迁移到更多其他任务。

提高对神经网络的理论理解。我们可以研究为什么随机初始化的前馈网络似乎包含中奖彩票，以及增加对优化和泛化的理论理解。