AI时代到来 如何提高孩子创造未来的能力

之前分享过创新工场人工智能工程院执行院长王咏刚的《AI时代，提高孩子创造未来的能力，陪孩子玩什么游戏？》一文。很多家长看了文章后，想知道玩这些游戏到底有什么用？

咏刚的这篇文章在解答这个问题的同时，再介绍了几个最近陪孩子玩过的游戏，算是上一篇文章的续篇。在此分享给大家，希望可以帮助到AI时代焦虑的父母们。

玩这些游戏有什么用？

如此发问的，大概有两类人：一类是对孩子教育有些焦虑的家长，觉得文章内提到的游戏和孩子的日常学习关系不大，或者说，与孩子学习成绩关系不大；另一类是线上线下儿童教育平台、知识分享平台的从业者，他们的疑问更专业些——你这些游戏教学法背后的设计思想和方法论是什么？这些游戏所训练的思维逻辑与现实的关联在哪里？比如，孩子玩汉诺塔游戏时建立的思维方法，未来在什么地方可以用到？

这些都是特别好的问题。但我的回答呢，也特别简单：

我陪我们家小朋友非非玩的游戏，其实就是一个既爱玩也有好奇心的爸爸，陪一个同样爱玩也同样有好奇心的儿子体验世界的过程。我想把它记录下来，写成文章。

这些游戏和孩子的日常学习关系不大，和孩子的学习成绩也基本无关。

这些游戏背后没有什么设计精妙、条理清晰、层次分明的教育学理念或方法论。毕竟我只是一个工程师兼业余写作爱好者，而不是教育学家。

这些游戏与现实的最大关联就是——我希望孩子能从小学会用正确的视角和正确的逻辑去理解这个神奇的世界，理解这个浩瀚宇宙中最有趣的事儿、最有趣的人。

正确的视角和正确的逻辑，这就是我上一篇文章所强调的“稀缺性技能体系”的核心基础。千万不要用功利主义或实用主义的方式去理解这种“稀缺性技能体系”，那只会让我们逐渐远离这些游戏的“初心”。

比如上一篇文章重点谈到的汉诺塔游戏——孩子在玩游戏时，大致可以建立模糊的、初步的“分而治之”的思想，体验一个整体任务及其嵌套或循环执行的子任务之间的关系。你知道游戏有趣、孩子喜欢就行了。如果你非要问“分治法”“迭代法”“递归法”到底有什么现实关联，那不就好比学了微积分却被老妈追问“这玩意儿能用来买菜还是能用来算账”？

实际上，“分治”“迭代”“递归”都是重要的思维逻辑，你学高数会用得上，你编程序会用得上，你设计生物学实验会用得上，你组织安排一个大型会议的运营细节会用得上，你设计一幢现代建筑会用得上，你创作一部草蛇灰线、伏延千里的小说会用得上，你为一个微信小程序做交互和视觉设计时也会用得上……可这种“用得上”或者说“现实关联”，肯定不是“学会用电动螺丝批就能在装配流水线上岗”那种意义上的现实关联。

我所看重的现实关联，更多指的是 “认知能力”“创造能力”以及“解决问题的能力”。

这个道理，懂的人自然懂。

AI时代正在到来。简单、重复性劳动必将被机器取代。等到你我的孩子渐渐长大，你会希望他们怎么融入全新的世界？你会希望他们怎么感受人生的价值和意义？作为宇宙中最“孤独”的智慧生物，你们，我们，你们的孩子，我们的孩子……如果大家能享受哪怕一丁点儿理解这个宇宙运行规律的快乐，或者在太阳系的尺度内创新、创造的快乐，或者在相互欣赏、喜欢的人之间分享思想与情感的快乐，这些还不够有价值、有意义吗？

所以，开心地陪孩子玩游戏就好；想那么多有的没的，岂不徒增烦恼？赶快进入正题——再介绍几个最近我陪非非玩过的游戏，算是上一篇文章的续篇。

培养理性认知：从积木游戏里看世界

人类对这个世界最直接的主观感受，经常与现象背后的科学逻辑大相径庭。每个人从小长大，也总会有一个不断用理性思维去反对主观印象的过程。

两千多年前的人类看到大地是平的，绝大多数人会自然而然地相信“天圆地方”或“天圆地平”，但古希腊思想家和科学家却可以通过更精妙的观察和实验证明地球是圆的，甚至测量地球这个球体的大小。

小朋友非非喜欢一边玩地球仪，一边听我讲埃拉托斯特尼测量地球周长的故事。尽管他现在还完全不懂平行线、内错角等几何知识，但他还是能从下面这张维基百科的示意图中，体会到埃拉托斯特尼在设计这个测量方法时的大胆假设和缜密构思。

非非没必要记住埃拉托斯特尼具体的实验设计和计算方法，他只要知道，人类的主观经验——例如地球是平的还是圆的——必须用科学方法、科学逻辑来证实或证伪就可以了。事实上，我经常通过玩游戏的方法，来帮助非非强化“经验不等于科学”的基本常识。

例如，我和非非玩过一个用立方体小积木来造火箭和宇宙飞船的游戏。这游戏用任何接近立方体形状的小积木都可以玩，玩法也特别简单，关键在于引导孩子做出自己的预测，然后再动手来证实或证伪。

我和非非先从最简单的造火箭开始。我用5块积木拼出一个概念意义上的小“火箭”，然后让非非把火箭长度增加一倍。这极其简单，非非不用动手就知道，要拼出一个有原火箭两倍长的新火箭，就需要用10块积木，因为5x2或者5+5都等于10。

建立了简单的概念，我开始给非非“出难题”了。现在，我打算造的是一艘金字塔形状的“宇宙飞船”——因为不考虑空气阻力，宇宙飞船当然可以打造成任意形状。金字塔形状的宇宙飞船，可以参考电影《星球大战》中的帝国级歼星舰。我先用立方体积木搭出了一个三层高的宇宙飞船，就像下图这样：

然后我让非非数一下，这个三层高的宇宙飞船，一共需要几块积木。答案是14块。那么，现在问题来了：我问非非，如果照这个样子，搭建六层高的宇宙飞船，大概需要几块积木？如果搭建九层高的宇宙飞船呢？

非非很积极地抢答：六层高的宇宙飞船比刚才的宇宙飞船高了一倍，刚才需要14块，那现在大概需要20多块积木吧；九层高的宇宙飞船又增高了三层，肯定会需要30多块吧（非非似乎是想计算14x3，但他的乘法还不过关）。

我提醒非非仔细想想，看这样的估计有什么问题没有。非非歪头想了一会儿，好像发现了什么。他说，六层的金字塔形积木，需要更大的底座来支撑整个高度，虽然高度上增加了三层，但用到的积木，可能比20多块多吧？我问他，那你猜会需要几块呢？他说，也许六层的需要40多块，九层的需要90多块吧。

到底非非的猜测靠不靠谱呢？动手验证一下就好呀。

六层的金字塔形宇宙飞船，非非花了好一阵功夫才搭完。他反复数了两遍，惊讶地发现，这个看上去不太大的家伙，居然花掉了91块积木——和他猜测的40多块积木相差甚远。九层宇宙飞船的建造难度和用料数量，就更加超出非非的预期。我们在客厅地板上搭了很久，直到耗尽了家里所有的立方体积木，也没能最终完成，因为九层飞船总共需要285块积木。

大人们可能对这种数字小把戏不以为然——这不就是乘方运算在起作用吗？一年级的小孩子又没学过乘方，当然搞不清其中的规律了。其实，这件事真的与我们所处的年龄段无关，因为很多人终其一生，还总是会在类似的地方犯错误，或总是选择性地相信主观经验、拒绝科学逻辑。

古代世界七大奇观之一的罗得岛太阳神铜像，是由当时的著名雕塑家林多斯的查尔斯（https://en.wikipedia.org/wiki/Chares_of_Lindos）设计的。据传，当时罗德岛人曾问查尔斯，如果雕像高50英尺，需要多少建造经费。查尔斯回答了一个数字。罗德岛人追问道，如果我们把雕像造得更大，高度达到100英尺，需要多少钱呢？查尔斯非常自信地说，高度增加了一倍，经费也增加一倍就行了。

查尔斯对建造经费的预估，与六层的金字塔形飞船需要多少积木，难道不是一模一样的问题吗？很不幸，擅长雕塑的查尔斯并不擅长科学思维，或者说，他和非非一样更习惯从表象出发而不是从科学规律出发想问题。在传说中，林多斯的查尔斯的结局是悲剧性的——他在实际建造过程中发现工程花费远超预算，他无法面对罗德岛人，更无法面对自己作为最好雕塑家的名誉，在雕像完工前就自杀身亡。

有一次我们在天津港玩的时候，正好遇到两艘豪华邮轮就近停靠，一艘是歌诗达邮轮大西洋号，另一艘是皇家加勒比邮轮海洋量子号。朋友中有人事先从官网查到了两艘邮轮的信息——大西洋号排水量86000吨，海洋量子号排水量167800吨。也就是说，海洋量子号的重量大约是大西洋号的两倍。抵达天津港前，朋友们纷纷猜测，港口中停靠的两条大船在视野中的尺度一定相差悬殊。哪料到，真到港口一看，两条船的大小其实也差不了多少嘛。视野中，两条船的比例关系大致如下图所示：

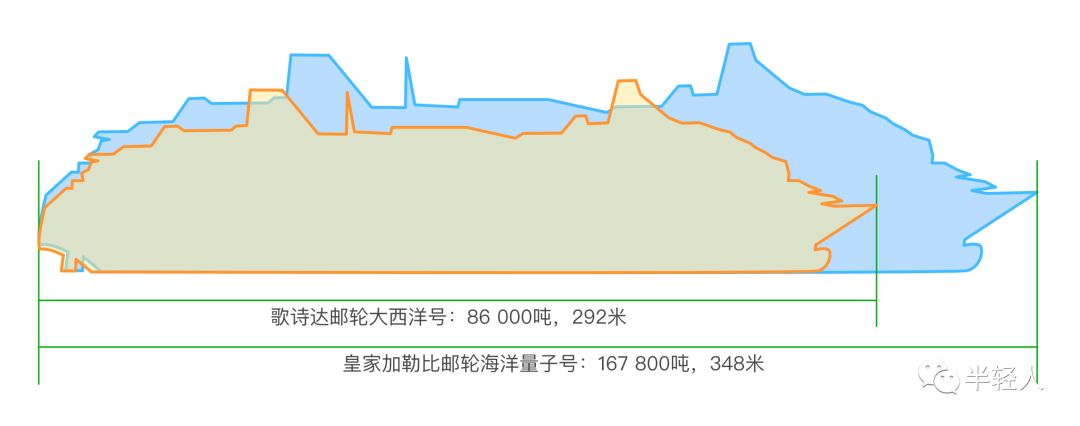
为什么体重相差悬殊的两条船在尺寸上的差距并不明显？这件事在原理上与我和非非建造三层、六层或九层的积木飞船也是一模一样的。三维物体在体积或重量上的两倍之差，反映到一维尺度上，通常就只有大约1.26:1的差距，因为：

显然，并不是每个大人都能在需要理性推理的时候想起乘方规律，而忘掉主观经验的。从这一点上说，非非在估计积木数量时所犯的错误，大人们也很难避免。

除了体积和长度的关系，大尺度的空间距离也比较难于通过主观经验来认知。小朋友生活中接触的距离单位，通常只是米、公里等等。一旦距离尺度扩展到天文单位，小朋友往往就很难想清楚，到底某个东西有多大，或到底某个东西有多远。

每逢农历十五，非非常指着天上说，月亮离地球好近呀。我说，月亮离地球的平均距离有38万公里呢。这时非非就会问，38万公里有多远呀？是有好几个中国到美国那么远吗？我说，嗯，不止有好几个，大概好几十个那么远吧。非非接着问，那，地球到太阳的距离，就有好几百个中国到美国那么远了吧。我说，那可不止，地球到太阳的距离，足有一万多个中国到美国那么远呢。非非总是稍显困惑地说，一万多个中国到美国那么远……那……到底有多远啊？

一二年级的小朋友对数量级的概念还相对模糊，要弄清一个特别大的数字到底有多大，或者弄清一个特别小的数字到底有多小，对他们来说绝对是一件挺有挑战的事儿。经常见到几个小朋友互相比谁说的数字更大（其实是小朋友间的一种“吹牛”游戏）：有的说，一百最大；有的说，一万比你的一百大；有的说，一万万最大；有的说，一万万万比一万万还大些……

其实，小朋友不容易搞清楚一万到底比一百大多少，大人也未必能准确理解一光年比一个天文单位远多少。这其实也是我们的主观经验在作怪。我们在日常生活中感知的数字尺度，远无法覆盖天文学上常见的尺度关系。但这并不意味着我们不能利用简单的游戏，帮小朋友培养正确的尺度或数量级的概念。

我和非非曾用乐高积木作为基本道具，玩宇宙飞船飞越太空的小游戏。一个乐高1x1标准积木块的长、宽大约是8毫米（参见https://en.wikipedia.org/wiki/Lego）。我和非非就将8毫米的尺度，称为一个“积木单位”。

假设地球的大小（直径）是1积木单位，那么，月亮离地球有多远呢？利用地球平均直径12742公里和地月平均距离384401公里之间的比例关系，很容易计算出，地月平均距离是30积木单位。我和非非一起在桌上摆了30个乐高积木。现在，从地球到月球的距离尺度就一目了然了：

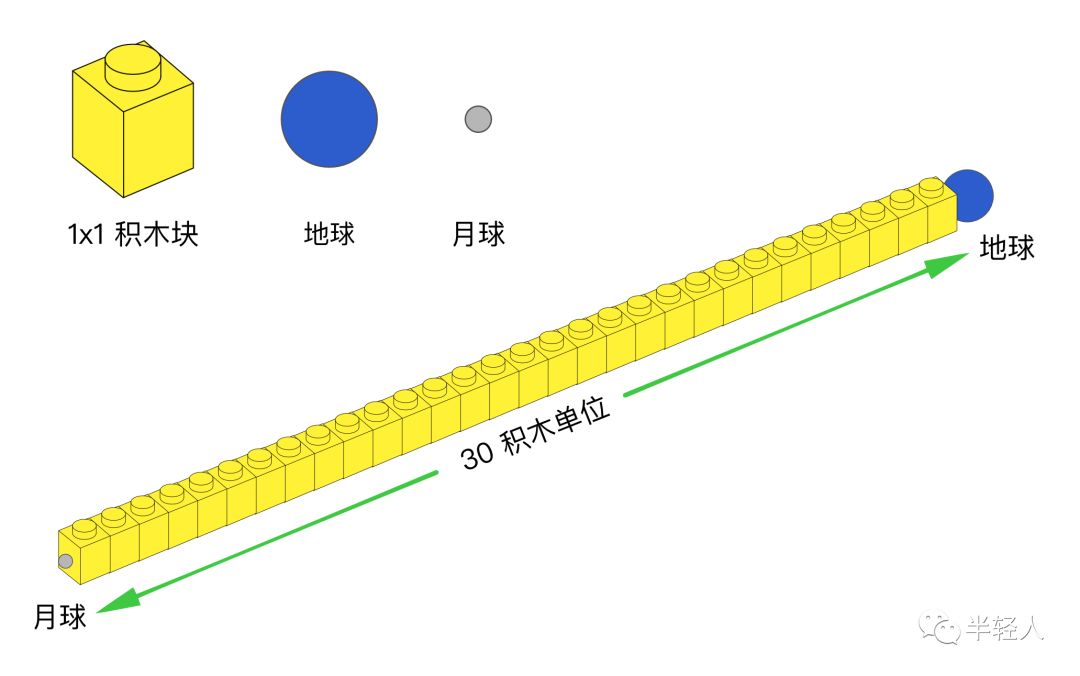
类似的，如果地球的大小（直径）是1积木单位，那么，在我和非非的积木度量体系里，太阳该有多大呢？简单的计算可知，太阳的大小应该是109积木单位。我们把一个1x1乐高积木放在桌子上，然后在旁边堆砌起109层的“乐高塔”（因为太高，很难用1x1的积木垂直堆叠，实际上可以考虑用2x3或2x4的积木块交错堆砌成高塔的形状），来直观地感受地球和太阳之间的“高度差”：

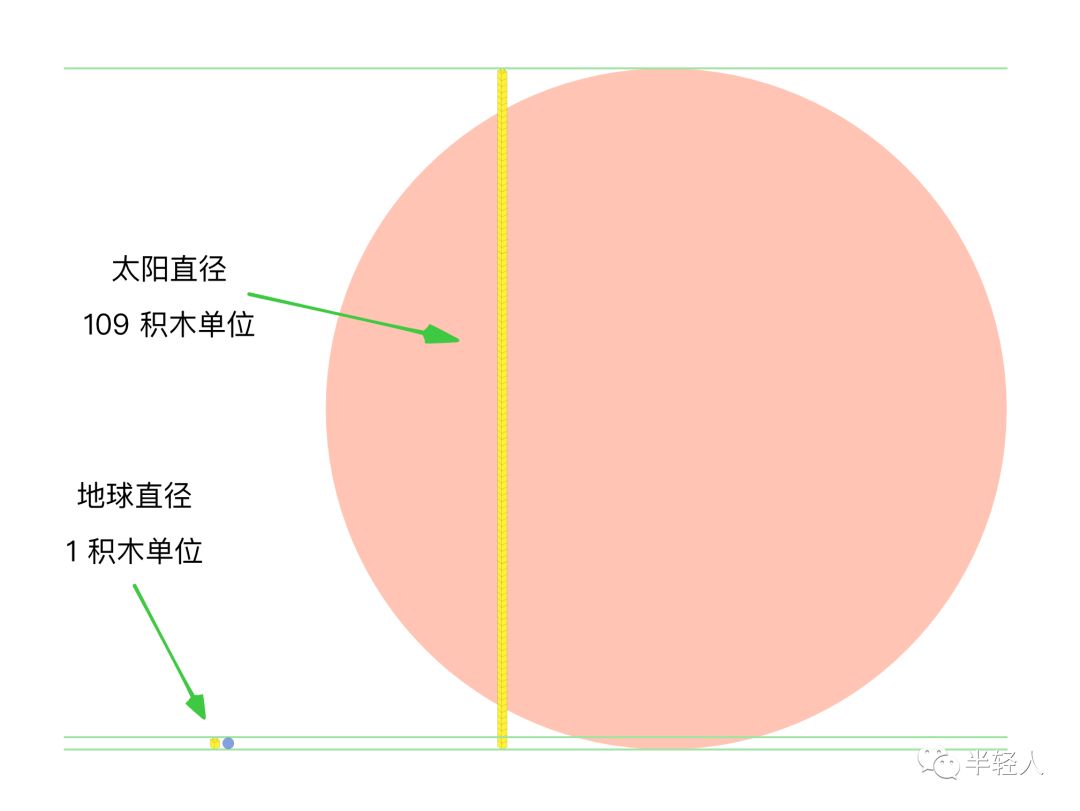
那么，在我们的积木度量体系里，地球与太阳之间的距离有多远呢？计算可知，大约是11700积木单位。1积木单位是8毫米，11700积木单位大约是94米远。为了直观地体验这个距离，我跟非非在楼下小区院子里玩的时候，会让非非手中拿着1x1的积木块表示地球，然后指着院子另一头的一个小朋友对非非说，你看，这个院子纵向的长度（我们的小区比较狭长）差不多100米，站在那一头的小朋友身高大约1米。如果你手上的积木块是地球，那么，太阳大约就在那个小朋友所站的位置，而太阳的大小就和那个小朋友的身高差不多。非非对这个距离尺度特别惊讶，因为太阳和地球之间的距离比他的想象远很多。他兴奋地举着积木，模仿地球一边自传，一边绕着大约100米开外的“太阳”公转——当然，他转不了很远，因为这个公转圆周已大大超出了小区院子的狭窄边界。

用积木建造金字塔飞船是为了让小朋友体验数学规律与经验认知的关系，而用积木来度量星球的大小或距离则是为了让小朋友体验天文尺度与经验认知的差别。两个游戏看似不同，但本质上都是为了帮小朋友建立正确的科学常识，培养从科学视角观察世界的好习惯。

理解信息与计算：自制二战水准的密码机

我们家小朋友非非喜欢聊历史、聊战争。二战时的著名战例、著名武器，还有二战前后的科技发展，他都特别着迷。大概是因为看到中途岛海战纪录片里提到了美国破译日军密码的故事，非非有段时间就特别关心二战时有线、无线通讯的加密与解密。于是，我给非非讲了二战时德国人设计、制造当时最复杂的加解密工具——恩尼格码密码机（https://en.wikipedia.org/wiki/Enigma_machine）的故事。

以二战时的标准来看，恩尼格码密码机的设计、制造简直就是机械式信息处理机的巅峰之作。非非特别喜欢对着历史照片，端详恩尼格码密码机里设计巧妙、制作精密的键盘、转子、反射器、接线板：

最重要的是，恩尼格码密码机的设计思路体现了很多信息学、计算机科学的基本思想。虽然通用计算机在二战时尚未问世，但今天在程序设计中使用到的很多基本逻辑、基本方法，其实都可以在恩尼格码密码机找到对应的设计。我觉得，从最简单的加密解密入手，不但可以跟孩子一起玩“军事情报大战”的游戏，还可以让孩子在玩耍中，逐渐熟悉数据、指令、编码、解码等现代信息学和计算机科学要素。

我和非非的“军事情报大战”游戏从最最简单的替换密码开始。我们要加密的情报是一个手机号码。非非很清楚，中国手机号码是由11位十进制数字组成的，每一位数字有0~9总共10种可能性。所谓替换密码，就是用一个密码本，将待加密的每一位数字，都替换成另一个数字。这个密码本其实就是一个一一对应的小表格，比如，把0替换成3，把1替换成2，把2替换成6……解密的时候，就用完全相反的过程，先把密码本翻转过来，变成一个解码表，然后从加密后的电话号码里，查找每一位密文对应的原始数字是多少。

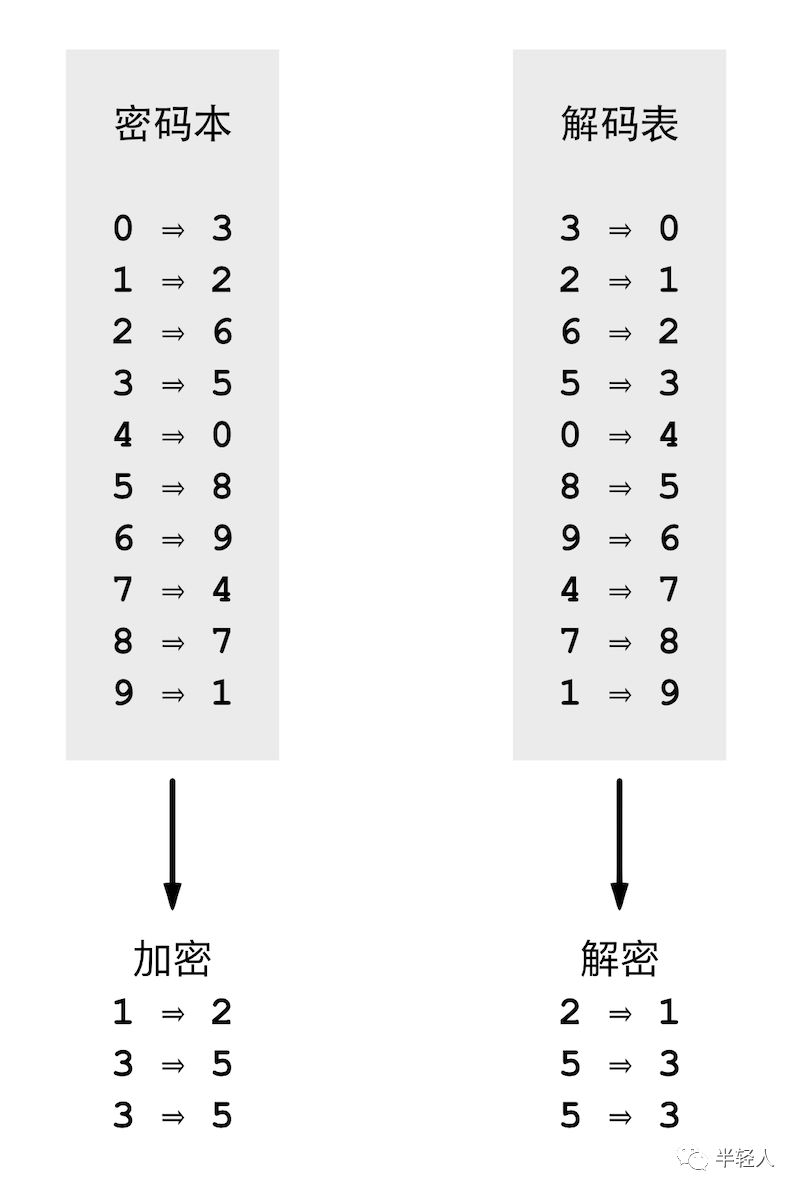
非非很快就掌握了制作这种密码本的方法。上图是非非制作的很多个密码本中的一个。当加密一个“133xxxxxxxx”的电话号码时，先查密码本，比如得到“133”对应的密文是“255”，然后非非把加密后的数字写在纸上，封装在信封里，神秘兮兮地假扮成战地通讯兵送给我解密，我拆开信封，查解码表得到原文“133”。

替换密码非常简单，在大多数情况下也很容易破解。但是，与小朋友玩替换密码的目的不在于真的加密一份情报，而是让小朋友潜移默化地理解以下几个信息学和计算机科学的基本概念：

信息可以用不同的编码方法来表达。有时候，简单变换编码方法（比如用字符“3”表示十进制的“0”）在效果上就是一种加密。

用某种编码表达的一份信息，可以被送给一个处理信息的人（比如上面游戏中负责加密信息的情报员），也可以被送入一个处理信息的机器（比如密码机或通用计算机），这份信息可以被称为“输入信息”。

人或机器可以用特定的“操作”对信息进行处理（比如上面游戏中的加密和解密操作）。

处理后的信息，可以用特定的编码方式呈现或显示出来（比如上面游戏中经过加密的“密文”或经过解密的“明文”）。

现代计算机在本质上就是一台读取信息、处理信息再输出信息的通用机器。

玩了几次替换密码，非非并不满足。他不停追问，恩尼格码密码机肯定不会这么简单吧？当然，德国人设计的军用恩尼格码密码机虽然属于替换密码的一种实现方式（多表替换密码，Polyalphabetic cipher），但复杂度远远超过我和非非玩的简单加解密游戏。不过，要理解恩尼格码密码机的实现原理也不算很难，用纸板、剪刀和笔，其实就可以动手制作一个简化版的恩尼格码密码机。

首先，恩尼格码密码机里有一个关键部件——反射器。“反射”在这里的意思就是将要加密的字符每两个一对儿地连接在一起，互相作为对方的密文或明文。这样做的好处是，加密和解密可以用完全相同的操作，查询完全相同的“密码本”——事实上，二战时使用恩尼格码密码机的操作员，无论为原文加密，还是为密文解密，都会按照密码本的约定设置好当天的接线板、转轮位置等，然后直接在键盘上输入原文或密文，并从指示灯中读出相应的密文或原文。

反射器的原理可以用一个数字纸盘和一个外接圆环来简单模拟。如下图所示，中央白色圆盘上的数字0~9在外圈蓝色圆环中被两两连接在一起。初始状态下，0与3的连接既可以表示原文“0”对应于密文“3”，也可以表示原文“3”对应于密文“0”。白色的中央圆盘和外圈的蓝色圆环组成了一个最简单的反射器，同时也定义了初始状态时的密码本。

恩尼格码密码机的一个复杂之处在于，每加密一个字符，密码本都会变化一次，这种变化，可以由字母转轮的转动来实现。回到上图中圆盘和圆环的例子，我和非非用纸板剪成圆形，组装成上图的样子，中央圆盘可以旋转。这时，当我们在初始位置对第一个字符进行了加密（比如将“1”加密成“5”）后，中央圆盘就必须顺时针旋转一格。旋转后，外圈圆环定义的反射关系，就变化成了另一种方式。我们在这个状态下，将电话号码的第二个数字“3”加密成“1”。下一步，中央圆盘再转一格，这时要加密的电话号码第三个数字虽然还是“3”，但加密结果已经变成了“9”。——每加密或解密一个字符，密码本就变化一次，这其实就是恩尼格码密码机的精髓所在了。

真实的恩尼格码密码机使用了多个转轮，这增加了密码本的复杂度。我和非非的“纸板密码机”其实也可以模拟多个转轮的情况。下图展示了我们在中央白色圆盘和外圈蓝色圆环之间，多引入了一个绿色转轮后的样子。绿色转轮上，我和非非画了一些或直接连接，或交叉连接的线条，把中央圆盘的数字和外圈圆环的线路端点连接起来。这样一来，从中央圆盘的一个数字出发，通过绿色圆环，再通过蓝色圆环，然后依次返回到另一个数字，整个路径变得大为复杂。每次加密一个字符后，中央圆盘就顺时针转动一格，这时，每两个字符之间的连接或对应关系就与上一个位置大为不同。为了增加复杂度，夹在中间的绿色圆环也可以在特定时候转动——比如，中央圆盘每转动10次，绿色圆环就转动1次。

基于我们的“纸板密码机”，如果把10个数字扩展到A~Z的26个字母，再把绿色圆环从1个扩展到3个、5个或更多，其复杂度就和二战时德国人使用的恩尼格码密码机差距不大了。

恩尼格码密码机利用转轮和连线组成动态变化的密码本，这个技巧让非非小朋友大呼神奇。能够在纸板上简单重现恩尼格码密码机的实现原理，对喜欢历史也喜欢科技的小朋友来说，是非常有趣的体验。当然，最重要的还是要让小朋友在这个游戏的过程里，亲自感受信息处理的基本逻辑。经过了这样的游戏体验，未来小朋友肯定更容易理解 “数据” “指令” “编码”“解码”等概念。

信息检索的奥秘：搜索引擎角色扮演

自从在学校里学过拼音并能用键盘输入汉字之后，我们家非非就经常在谷歌或百度上搜索他喜欢的信息，比如蜥蜴有多少种，战列舰有几门主炮，古代青铜器上的花纹长什么样，最早的个人电脑和今天的电脑有何不同，等等等等。搜索得多了，非非有一次就好奇地问我，谷歌和百度这样的搜索引擎，到底是如何在那么短的时间里，找到许多许多信息的？

这真是一个好问题！非非虽知道我曾在谷歌工作过很多年，也去谷歌总部和谷歌北京的办公室玩耍过，可他此前并不太清楚谷歌到底是做什么的。他能一边使用搜索引擎，一边主动提出关于搜索引擎的问题，这还真是让做过很多年搜索相关算法的我大为感动呢。

当然，感动归感动，到底该如何向七八岁的小朋友科普搜索引擎知识呢？到底是具体的搜索算法更重要，还是人类数千年来摸索的信息组织和管理思想更重要？有没有可能通过一个好玩的游戏，让小朋友自己来了解组织信息的基本手段？

我和非非拿出白纸，开始玩一个“搜索引擎角色扮演”的小游戏。我把白纸裁成8片，让非非在每片纸上写一个编号。我将每片纸称作一个“信息盒子”。然后，我在每个信息盒子里，用英文字母写上不同的信息，比如1号盒子里是“A”“B”“C”，2号盒子里是“C”“D”……如下图：

这时，我让非非扮演一个“搜索引擎”。非非心领神会，立即张开嘴巴，用手势示意，他的嘴巴就是搜索框，现在可以开始搜索了。作为用户，我提了几个从简单到复杂的搜索需求，分别是：

字母“F”在哪些信息盒子里出现过？

字母“A”在所有这些信息盒子里一共出现了多少次？

字母“A”和字母“B”同时在哪些信息盒子里出现过？

有没有哪个信息盒子同时包含了字母“A”、字母“C”和字母“E”？

对于这几个搜索问题，非非很快就找到了虽然笨拙、但肯定奏效的解决方案。他针对每个问题，都会从编号1到编号8，一个接一个地查看每个信息盒子里的信息，然后给出答案。

我问非非，如果按照你这种方式来实现搜索引擎，你觉得会有什么问题吗？非非回答，这样做太慢了，每次都要把所有信息盒子看一遍，如果信息盒子特别多，那要花多少时间啊。

我问非非，你用谷歌或百度时，输入一个查询，谷歌和百度回答你的速度有多快？非非说，特别快，几乎是一眨眼的时间。谷歌和百度一定不会像我一样每次都把所有信息盒子看一遍。

显然，真正的搜索引擎使用的是更聪明的方法。小朋友一旦意识到了这一点，自然就提起了极大的兴趣，非要刨根问底弄清楚。于是，我开始教非非如何为已有信息建立“倒排索引”。

我跟非非讲，搜索引擎建立索引的做法其实特简单，只是将原来的信息变换了一种组织方式。刚才我们看到的信息，是以每个信息盒子为单位的。为了更快地完成搜索，我们需要换一种信息的组织方式，即，我们从每个字母的角度出发，先创建一张表格，记录下每个字母到底在哪些信息盒子里出现过。这个表格的每一行对应一个字母，字母后面记录的是一组信息盒子的编号，表示这个字母在哪些信息盒子里出现过。如果一个字母在某个信息盒子里出现过两次，就把信息盒子的编号记录两次。倒排索引的建立方法不算难，非非很快就在纸上完成了倒排索引的编制：

利用倒排索引，稍加提示，非非快速掌握了搜索的技巧。要想搜索某个字母在哪些盒子里出现过，只要直接读出倒排索引中该字母对应的那一行就可以了。要想搜索某个字母在所有盒子中出现过几次，只要数一下该字母对应的编号个数就可以了。要想搜索某两个字母在哪些盒子里同时出现过，我们需要归并两个字母对应的编号序列，找出在两个序列里同时出现的那些编号。

玩了几次搜索引擎角色扮演的游戏，非非好像恍然大悟似地说，我知道了，原来把信息编制成索引，就可以又准又快地查找信息。那么说，我们上学时查的《新华字典》，其实也是一种索引啦，因为可以从一个字查到这个字的意思。确实，《新华字典》本身就是按拼音顺序编排的一种索引结构，虽然有别于搜索引擎的倒排索引，但也属于信息的一种有序组织方式。相比之下，专业书籍在书后所附的关键词索引，在功能上更接近搜索引擎一些。

陪孩子玩搜索引擎游戏，其实只是想让小朋友弄明白：

信息的组织方式可以有很多种。

有序的信息组织，可以大幅加快信息检索的速度。

搜索引擎的基本原理是用计算机来重新组织信息，并通过对索引的查询完成快速检索。

非非很快就把这种重新组织信息的技能举一反三，用在他熟悉的各种地方。比方说，他刚背过《道德经》开头几句。他发现，假设把每一句装进一个有编号的信息盒子，就可以用每个单字作为索引入口，建立起单字到句子编号的倒排索引，就像下图这样：

不过，玩搜索引擎角色扮演游戏也有一个副作用：非非小朋友对爸爸曾经在谷歌做的工作，彻底失去了神秘感。非非说，原来爸爸在谷歌做工程师，就是在开发这么一个程序呀。说这话的时候，非非一脸不屑。

要让非非对谷歌、百度之类现代搜索引擎的实现复杂度有一些认知，其实也不算太难。这部分得益于前面我们介绍过的“积木游戏”，即，如何让小朋友熟悉比较大的数量级或真实尺度。

我还是拿人工编排和使用倒排索引作为示例，跟非非一起讨论：一个小朋友最多可以为多少个信息盒子（或者说，多少要检索的网页）建立并管理索引？非非的猜测是100个。我接着告诉非非，根据公开数据估计，谷歌索引的网页数量，大概在几十到几百万亿的样子。既然每个人可以管理100个网页的索引，要想全部用人工来管理谷歌的所有网页，恐怕需要约一万亿人（这远远超出了地球上人类的总人口，有必要从邻近的外星球上把外星人也请过来）。

现在，假设我们有了足够多的可以建立和管理索引的人，我们的搜索引擎该如何建设呢？

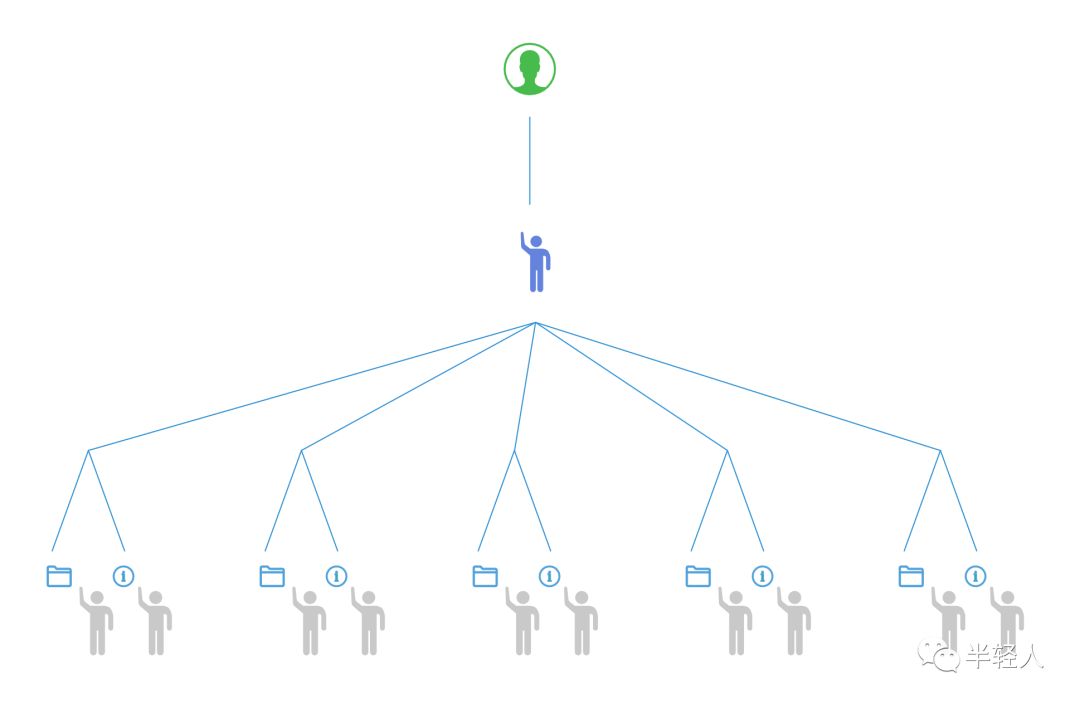
上图中，绿色头像代表搜索引擎的用户。灰色小人代表我们请来的一万亿人类与外星人志愿者大军，他们也被称为“工人”（Worker）。我们可以把工人分成两组，一组人专门建立和处理索引，一组人专门管理原始的信息盒子（网页），这两组工人既可以两两搭档工作，也可以分别在各自的大组中工作。这时，因为志愿者太多，我们不得不请来一名或多名“指挥官”（Master），见图中的蓝色小人。搜索引擎用户提出的搜索请求，要先发送给指挥官，然后再由指挥官分发给每个工人，工人根据自己管理的网页或索引，完成一部分搜索任务后，直接将结果返回给指挥官。一旦指挥官收到了所有工人返回的结果，就会将结果合并、去重、排序，然后返回给用户（注：这里对分布式索引和检索系统的Worker和Master工作原理的讲解仅为简化后的示意，与真实系统有较大差别）。

指挥官和工人的比喻，非非大概只能理解个皮毛。但通过这样的讲解，非非还是可以约略知道，原来爸爸在谷歌时所写的程序，并不似想象中那么简单。重要的是，这样的讲解可以在非非心里埋下一颗将复杂任务分而治之的种子，这种子将来发芽长大时，小朋友与现代计算机科学里最重要的概念之一——分布式计算——之间就没有太多隔阂了。

少谈教育，多玩游戏

上一篇《AI时代，提高孩子创造未来的能力，陪孩子玩什么游戏？》内容稍杂了一点，既有训练逻辑思维的游戏，也有训练语言能力、表达能力乃至创造力的游戏。这一篇作为续篇，我只介绍了与科学认知、信息学和编程逻辑这三方面相关的小游戏。接下来，我还是会不定期地把我和非非常玩的游戏记录下来，以续篇的形式发出，但每个续篇会有不同的侧重方向——也许，下一篇可以集中讨论语言和表达能力？

有人质疑我写的这些游戏的可操作性和可复制性。比方说，有人就问过我，你这些游戏看上去挺好，但如果家长的数学不好或编程不好，该怎么陪孩子玩，怎么引导孩子呢？你有没有类似教学大纲或教学参考书之类的东西？

很遗憾，我既不知道类似问题的答案，也没有教学大纲或教学参考书。

我把我与非非小朋友常玩的，有关逻辑思维训练或科学认知训练的游戏记录下来，只是想和大家分享这些有趣的经历。我不是教育学家，不知道该如何将教育方法变成任何人都很容易获取的“用户手册”。另一方面，我也不愿看到有趣的游戏摇身变成枯燥、呆板的条条框框。

这个世界已拥有太多的程式化教育，何必再添一门让小朋友皱眉的乏味功课呢？

孩子们能从游戏里感悟、领会到有趣的知识，学到有用的思维方法，当然最理想不过。但就算孩子只能体会到游戏本身的快乐，这快乐又何尝不是一种珍贵的童年记忆呢？

游戏就是游戏——让我们少谈教育，多玩游戏。