关于距离计算的总结

距离计算在自然语言处理中得到广泛使用，不同距离计算方式应用与不同的环境，其中也产生了很多不同的效果。

1 余弦距离

余弦夹角也可以叫余弦相似度。集合中夹角可以用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。

余弦取值范围为[-1,1]。求得两个向量的夹角，并得出夹角对应的余弦值，词余弦值就可以用来表示这两个向量的相似性。夹角越小，趋近于0度，余弦值越接近于1，它们的方向就更加吻合，即更加相似。当两个向量的方向完全相反时，夹角的余弦取最小值-1。当余弦值为0时，两向量正交，夹角为90度。因此可以看出，余弦相似度于向量的幅值无关，于向量的方向相关。

公式描述：

Python代码实现：

 import numpy as np # np.dot(vec1,vec2) 量向量（数组）：两个数组的点积，即元素对应相乘后求和 # np.linalg.norm(vec1)：即求vec1向量的二范数（向量的模）  vec1 = [1,2,3,4] vec2 = [5,6,7,8] dist1 = np.dot(vec1, vec2)/(np.linalg.norm(vec1)*np.linalg.norm(vec2)) print("余弦距离测试结果为：\t"+str(dist1))

2 欧氏距离

欧几里得距离即欧几里得空间中两点间的直线距离。

Python实现：

 import numpy as np vec1 = np.mat([1,2,3,4])        # 生成numpy矩阵 vec2 = np.mat([5,6,7,8])  # 根据公式求解1 dist1 = np.sqrt(np.sum(np.square(vec1 - vec2))) print("欧式距离测试结果是：\t"+ str(dist1))  dist2 = np.sqrt((vec1-vec2)*(vec1-vec2).T) # 根据公式求解2 print("欧式距离测试结果是：\t"+ str(dist2))

3 曼哈顿距离

曼哈顿距离也成为城市街区距离。用来表示两个点在标准坐标系上的绝对轴距之和，即从一个路口到另外一个路口，驾驶距离不是两点之间的直线距离。

Python实现

 import numpy as np  vec1 = np.mat([1,2,3,4]) vec2 = np.mat([6,7,8,9]) dist = np.sum(np.abs(vec1 - vec2)) print("曼哈顿距离测试结果是：\t"+str(dist))

4 明可夫斯基距离

明氏距离又叫明可夫斯基距离，是欧氏空间中的一种测度，被看作欧氏距离和曼哈顿距离的一种推广。

当p=1时，就是曼哈顿距离

当p=2时，就是欧氏距离

当p=3时，就是切比雪夫距离

python实现

可参照之前代码

5 切比雪夫距离

python实现

 import numpy as np vec1 = np.mat([1,2,3,4]) vec2 = np.mat([5,6,7,8]) dist = np.max(np.abs(vec1 - vec2)) print("切比雪夫距离测试结果是：\t" + str(dist))

6 杰卡德距离

杰卡德（Jaccard）相似系数：两个集合A和B的交集在元素在A、B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示。杰卡德距离：在占比中所取的是两个集合中不同元素。

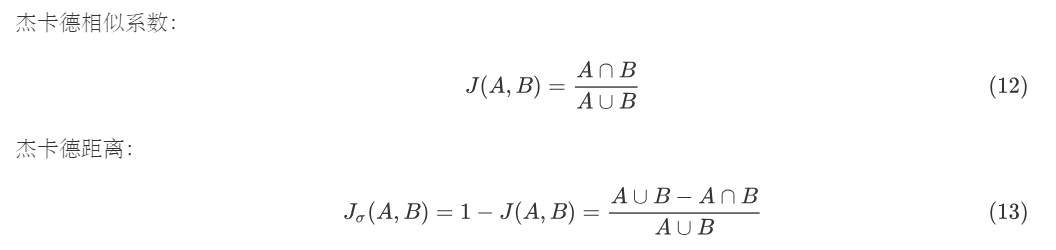
Python实现：

 import numpy as np v1 = np.random.random(10) > 0.5
        # 生成10个true false数据（即0，1） v2 = np.random.random(10) > 0.5 vec1 = np.asanyarray(v1, np.int32)
        # 转换位0、1矩阵 vec2 = np.asanyarray(v2, np.int32) # 距离计算 up = np.double(np.bitwise_and((vec1 != vec2),np.bitwise_or(vec1 !=0,vec2!=0)).sum())
        # 涉及到数学逻辑运算 down = np.double(np.bitwise_or(vec1 !=0 ,vec2!=0).sum())
        # 取并集, (vec1 !=0 ,vec2!=0)先转对应元素为true ，false的矩阵 dist = (up/down) print("杰卡德距离测试结果是：\t"+str(dist))

7 汉明距离

在信息论中，两个登场字符串之间的汉明距离对应位置上的不同字符的个数。也就是说，将一个字符串变换成另一个字符串所需要替换的字符个数。

例如：“toned”与“roses”之间的汉明距离就是3

python实现：

 import numpy as np v1=np.random.random(10)>0.5 v2=np.random.random(10)>0.5 vec1=np.asarray(v1,np.int32) vec2=np.asarray(v2,np.int32) dist=np.mean(vec1!=vec2)
        # 取均值 print("汉明距离测试结果是:\t"+str(dist))