

Pedro Domingos教授的研究论文汇集机器学习研究人员的经验教训
电子说
描述
机器学习算法被认为能够通过学习数据来弄清楚如何执行重要任务。
这意味着数据量越大,这些算法就可以解决更加复杂的问题。然而,开发成功的机器学习应用程序需要一定的“民间技巧”,这在教科书或机器学习入门课程中很难找到。
Pedro Domingos教授的一篇很好的研究论文,该论文汇集了机器学习研究人员和从业者的经验教训。
1.学习=表示+评估+优化
你有一个应用程序,你认为机器学习可能是一个很好的选择。现在,在机器学习领域,每年都会有大量的机器学习算法可供选择,有数百种机器学习算法问世。应该使用哪一个?
在这个巨大的空间中不迷失的关键是要明白所有机器学习算法的都由三个核心要素组成:
表示:输入数据,即要使用的特征,学习器和分类器必须以计算机可以理解的语言表示。学习器可以学习的分类器集称为学习器的假设空间。如果分类器不在假设空间中,则无法进行学习。
澄清说明:分类器与学习器的含义是什么?假设你有训练数据,并使用你构建另一个程序(模型)的程序处理这些数据,例如决策树。学习器是从输入数据构建决策树模型的程序,而决策树模型是分类器(能够为每个输入数据实例提供预测输出的东西)。
评估:需要评估函数来区分好的分类和坏的分类。算法内部使用的评估函数可能与我们希望分类器优化的外部评估度量不同(为了便于优化,并且与后面讨论的问题有关)
优化:最后,我们需要一种方法来在分类器中进行搜索,以便我们可以选择最佳的分类器。学习器效率的关键是选择优化技术。通常从使用现成的优化器开始。如果需要,以后你可以用自己的设计替换它们。
下表显示了这三个组件中每个组件的一些常见示例。
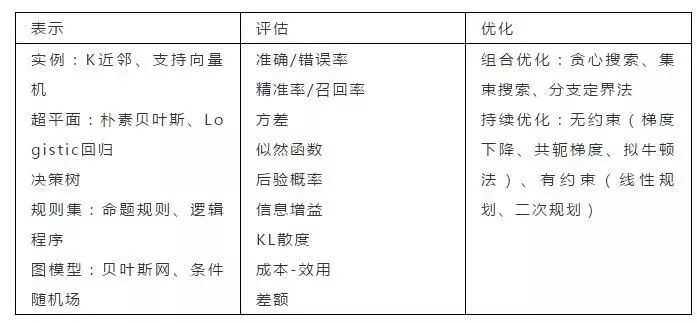
2.泛化才有用
机器学习的基本目标是概括超出训练集中的例子。因为,无论我们拥有多少数据,我们都不太可能在测试时再次看到这些确切的示例。在训练集上做得很好很容易。初学者中最常见的错误是测试训练数据并得到成功的假象。如果所选分类器随后在新数据上进行测试,则通常不会比随机猜测更好。因此,从一开始就设置一些数据,并且仅使用它来测试最终选择的分类器,然后在整个数据上学习最终分类器。
当然,保留数据会减少可用于训练的样本数。这可以通过交叉验证来缓解:比如,将你的训练数据随机分成十个子集,在训练其余部分时保持每个子集,在其未使用的示例上测试每个学习的分类器,并对结果求平均值,来看特定参数设置的效果如何。
3.只有数据还不够
当泛化是目标时,我们会遇到另一个主要后果:仅凭数据是不够的,无论你拥有多少数据。假设我们想学习一百万个例子中100个变量的布尔函数(0/1分类)。这意味着2 ^100-10^6个例子,你不知道它们的类。如果手头没有更多信息,这怎么能优于随机猜测呢?
似乎我们陷入了困境。幸运的是,我们想要在现实世界中学习的特性并不是从所有数学上可能的函数集中统一绘制的!实际上,非常一般的假设——就像具有相似类的类似示例——是机器学习如此成功的一个重要原因。
这意味着专业知识和对数据的理解对于做出正确的假设非常重要。对学习知识的需求应该不足为奇。机器学习并不神奇,它无法从无到有。它的作用是从更少的东西中获得更多。与所有工程一样,编程需要做很多工作:我们必须从头开始构建所有东西。学习更像是农业,让大自然完成大部分工作。农民将种子与营养物质结合起来种植农作物。学习者将知识与数据相结合以优化程序。
4.过拟合的多面性
过度拟合的问题是机器学习的问题。当你的学习器输出一个对训练数据100%准确但对测试数据只有50%准确的分类器时,实际上它可以输出一个对两者都准确度为75%的分类器,它已经过拟合。
机器学习中的每个人都知道过拟合,但它有多种形式,并不是很明显。理解过拟合的方法之一是将泛化误差分解为偏差和方差。
偏差是学习者一直学习同样错误的倾向。与真实信号无关,方差是学习随机事物的倾向。飞镖图比可以更好地理解这一点,如下图所示:
例如,线性学习器具有较高的偏差,因为当两个类之间的划分不是明确的超平面时,学习器无法正确地判别关系。决策树没有这个问题,因为它们的学习方法很灵活。但另一方面,它们可能有高度差异——在同一任务的不同训练数据集上学习的决策树通常是非常不同的,而实际上它们应该是相同的。
现在,如何处理过拟合?
可以在此处使用交叉验证,例如通过使用它来选择要学习的决策树的最佳大小。但请注意,这里还有一个问题:如果我们使用它来选择太多参数,它本身就会开始过拟合,我们又回到了同样的陷阱。
除了交叉验证之外,还有许多方法可以处理过拟合。最受欢迎的是在评估函数中添加正则化项。另一个选择是执行卡方等统计显著性检验,以分析添加更多复杂性是否会对类分布产生任何影响。这里的一个重点是没有特定的技术“解决”过拟合问题。例如,我们可以通过陷入欠拟合(偏差)的相反误差来避免过度拟合(方差)。同时避免两者都需要学习一个完美的分类器,并没有一种技术总能做到最好(没有免费的午餐)。
5.高维中的直觉失效
过拟合后,机器学习中最大的问题是维数的诅咒。这个表达式意味着当输入是高维的时,许多在低维度下工作正常的算法变得难以处理。
由于固定大小的训练集覆盖了输入空间的一小部分(可能的组合变得巨大),因此随着示例的维度(即特征的数量)的增长,正确泛化的难度呈指数级增加。但这就是为什么机器学习既有必要又有难度。正如你在下图所示,即使我们从1维过渡到3维,能够分辨出不同示例的工作似乎开始变得越来越难——在高维度上,所有示例都开始相似。
这里的一般问题是,我们来自三维世界的直觉使我们在高维度上失败。例如,高维度橙色的大部分体积都在外部,而不是内部!
令人难以置信的是:如果恒定数量的示例在高维超立方体中均匀分布,并且如果我们通过将其刻在超立方体中来近似超球面,则在高维度中,超立方体的几乎所有体积都在超球面之外。这是个坏消息。因为在机器学习中,一种类型的形状通常由另一种形状近似。
澄清注意:如果你对所有“夸大其词”感到困惑,超立方体内部的超球面看起来像是这样的二维和三维:
因此,你现在可以理解,构建2维或3维分类器很容易,但在高维度上,很难理解发生了什么。反过来,这使得设计好的分类器变得困难。事实上,我们经常陷入这样的陷阱:认为获取更多特征不会带来负面影响,因为在最坏的情况下,它们不会提供关于类的新信息。但事实上,维度的诅咒可能会超过它们的好处。
启示:下次当你考虑添加更多特征时,请考虑当你的维度变得太大时可能出现的潜在问题。
6.特征工程是关键
当一天结束时,所有机器学习项目中有成功的,也有失败的。它们之间有区别呢?这个不难想到,最重要的因素就是使用的特征。如果有许多独立的特征,并且每个特征都与类的相关性很好,那么机器学习就很容易。相反,如果类是需要通过复杂方式处理特征后才能被使用,那么事情就变难了,这也就是特征工程——根据现在输入的特征创建新的特征。
通常原始数据格式基本不能为建模所用。但你可以从中构建可用于学习的特征。事实上,这是机器学习项目中的最花精力的部分。但这也是最有趣的部分之一,在这里直觉、创造力和“小技巧”与技术是同样重要的东西。
经常会有初学者惊讶一个机器学习项目中花费在训练上的时间竟如此之少。但是,如果考虑收集数据,整合数据,清理数据并对其进行预处理的时间以及在特征选择上的试错次数,这个时间就相对合理。
更何况,机器学习在构建数据集和运行学习样例上不是一次性的过程,而是一个迭代的过程,需要运行学习样例,分析结果,修改数据或学习样例,以及重复上述过程。训练往往是最快的部分,但那是因为我们对这部分相当熟练!特征工程很难,因为它是专业领域的,不过学习器在很大程度上是通用的。当然,机器学习界的梦想之一就是提高特征工程的自动化程度。
7.丰富的数据胜过聪明的算法
假设你已经构建了一组最好的特征,但是你得到的分类器仍然不够准确。你现在还可以做什么?有两个主流的办法:
设计更好的机器学习算法或者是收集更多数据(更多样例,可能还有更多原始特征)。机器学习研究人员会去改进算法,但在现实中,通往成功的最快途径往往是获取更多数据。
根据经验,具有大量数据的傻瓜算法胜过一个具有适度数量的聪明算法。
在计算机科学中,通常情况下,两个主要的资源限制是时间和内存。但在机器学习中,还有第三个约束:训练数据。在这三个中,今天的主要瓶颈是时间,因为有大量的可用数据,但没有足够的时间来处理它们,所以数据被闲置了。这意味着在实践中,更简单的分类器会胜出,因为复杂的分类器需要很长的学习时间。
使用更聪明的算法并不会给出更好的结果,部分原因是在一天中它们都在做同样的事情,将所有学习样例基本上都是通过将相邻的样例分组到同一个类来工作的。关键的区别在于对“相邻”的定义。
当我们有非均匀分布的数据时,即使复杂的学习样例也可以产生非常不同的边界来对结果进行分类,最终它们仍然在重要区域做出相同的预测(具有大量训练样例的区域,因此也可能出现大多数文本样例)。正如下图所示,无论是花式曲线,直线还是逐步边界,我们都可以得到相同的预测:
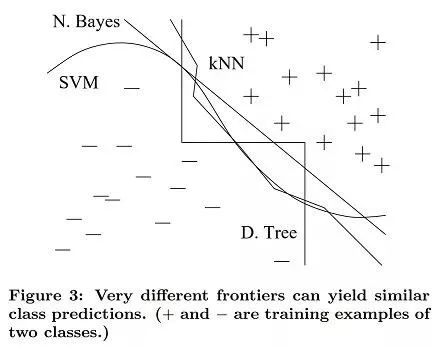
通常,首先尝试最简单的学习器(例如,逻辑回归前的朴素贝叶斯,支持向量机之前的邻近算法)。复杂的学习器很吸引人,但它们通常很难使用,因为它们需要控制更多的旋钮以获得好的结果,并且因为它们的内部更像是黑箱。
8.组合多个模型,而非只用一个
在机器学习的早期阶段,努力尝试使用多种学习器的各种变形,并选择最好的那个。但是研究人员发现,如果不是选择其中最好的单一模型,而是结合各种变形会得到更好的结果,建模者只需稍加努力就可以获得显著提升的效果。现在建这种模型融合非常普遍:
在最简单的技术称为bagging算法,我们使用相同的算法,但在原始数据的不同子集上进行训练。最后,我们取均值或通过某种投票机制将它们组合起来。
Boosting算法中学习器按顺序逐一训练。随后的每一个都将其大部分注意力集中在前一个错误预测的数据点上。我们会一直训练到对结果感到满意为止。
Stacking算法中,不同独立分类器的输出成为新分类器的输入,该分类器给出最终预测。
在Netflix算法大赛中,来自世界各地的团队竞相建立最佳的视频推荐系统。随着比赛的进行,发现将学习器与其他团队相结合可以获得了最佳成绩,并且合并为越来越大的团队。获胜者和亚军都是超过100个学习器的叠加集成,两个集成的结合进一步改善了结果。算法组合将更好!
9.理论保证和实际具有差异
机器学习论文充满理论保证。我们应该对这些保证做些什么?归纳法传统上与演绎法形成对比:在演绎法中,你可以保证结论是正确的,在归纳法中就很难说。最近几十年的一个重要进展是我们认识到可以做归纳结果正确性的保证,前提是如果我们愿意接受概率保证。
例如,我们可以保证,给定一个足够大的训练集,在很大的概率上,学习器会返回一个成功泛化的假设或无法找到一个保持正确的假设。
另一种常见的理论保证是给定无穷的数据,学习器可以保证输出正确的分类器。在实践中,由于我们之前讨论过的偏置-方差的权衡,如果在无穷数据情况下,学习器A比学习器B好,那么在有限数据的情况下B通常比A好。
理论保证在机器学习中的主要作用不是作为实际决策的标准,而是作为理解算法设计的起点。
10.简单并不意味着准确
在机器学习中,奥卡姆剃刀原理通常被认为是给定两个具有相同训练误差的分类器,两者中较简单的可能具有较低的测试误差。
但事实并非如此,我们之前看到了一个反例:即使在训练误差达到零之后,通过添加分类器,一个boosted ensemble的泛化误差也会继续改善。与直觉相反,模型的参数数量与过拟合之间没有必要的联系。也就是说在机器学习中,一个更简单的假设仍然应该是首选,因为简单本身就是一种优势,而不是因为它意味着准确性。
11.可表示不等于可学习
仅仅因为可以表示函数并不意味着可以学习它。例如,标准决策树学习器无法学习叶子多于训练样例的树木。
给定有限的数据、时间和内存,标准学习器只能学习所有可能功能的一小部分,并且这些子集对于不同表示的学习器是不同的。因此,这里的关键是尝试不同的学习器(并可能将它们结合起来)是值得的。
12.相关性不意味着因果性
我们都听说过相关性并不意味着因果性,但仍然有人常常倾向于认为相关性意味着因果关系。
通常,学习预测模型的目标是将它们用作行动指南。如果我们发现用户在超市经常买了啤酒就会买尿不湿,那么也许把啤酒放在尿不湿部分旁边会增加销量。但除非我们进行真实的实验,否则很难判断这是否属实。相关性标志着一个潜在的因果关系,我们可以将其作为进一步研究的方向,而非我们的最终结论。
结论
跟其他学科一样,机器学习有很多“民间智慧”,很难获得但对成功至关重要。
- 相关推荐
- 机器学习
-
求大神分享单片机从业的经验教训和学习历程?2021-09-18 0
-
借鉴开发人员累计的经验教训构建更出色的嵌入式系统2017-11-16 1121
-
工程师跨度13年、回顾194个bug总结的18条编码、测试和调试经验教训2018-02-27 1081
-
google机器学习团队开发机器学习系统Seti的一些经验教训2018-06-01 1683
-
研究人员实现无创早期肺癌筛查,以机器学习为基础2020-03-27 847
-
搜索工程师正在借鉴Microsoft AI研究人员的经验教训2020-04-20 1900
-
研究人员使用AI教机器人如何将物体交给人类2020-04-28 1742
-
研究人员通过AI和机器人来治疗手部震颤疾病2020-04-29 936
-
研究人员已经使用机器学习来开发血液测试2020-05-21 1961
-
70年人工智能研究,解读研究者最大的惨痛教训经验2020-08-14 506
-
研究人员使用低成本的柔性芯片制造了机器学习处理引擎2020-09-11 2119
-
研究人员开发了一种新型的磁力驱动高速软件机器人2020-10-10 2852
-
研究人员宣布了一种新的AI机器学习工具2020-11-23 1898
-
写在最前:单片机从业的经验教训和历程。2021-11-15 339
-
嵌入式微控制器应用中的无线(OTA)更新:设计权衡与经验教训2023-11-23 223
全部0条评论

快来发表一下你的评论吧 !

