揭秘合成器 解析电子打击乐器

在本系列的第一篇文章中我们介绍了声音的组成元素以及分解方式，从而回答了「谐波是什么？谐波从哪里来？」这一问题。我们用震荡的绳子类比谐波振荡器，讲解了每种旋律乐器最基本的发声原理。

在今后的文章中，你会了解到只需使用几个简单的谐波合成器就可以模拟（或者说「合成」）出许多「真实」的乐器。比如说，锯齿波（sawtooth wave）可以模拟出管弦乐团的铜管和弦乐音色、方波（square wave）可以合成出单簧管等木管乐器的音色，声音较为单薄的脉冲波（pulse wave）可以提供类似双簧管和巴松管的尖锐声音。

不光只有管弦乐器，相同的波形同样用于可以合成现代乐器。将锯齿波和脉冲波混合可以得到与真实贝斯吉他极其类似的音色；给经过适当调制的锯齿波加上一些效果器可以模拟出主音吉他的声音。当然，在演奏这些音色的时候你需要用与吉他类似的演奏技法才能保证听感尽量真实，但这不是本文要讨论的重点。重点在于：即使用一个只提供三种简单波形的合成器你也可以模拟出各式各样的音色。

不过，除了谐波振荡器之外，还有一类振荡器存在。这些「非谐波」振荡器和谐波振荡器一样重要，但它们两类的工作原理却大相径庭。包括爵士鼓、定音鼓以及许多民族乐器在内的打击乐器的声音在现代西方音乐中被频繁应用。为什么这些打击乐器的声音与旋律乐器的音色差别如此巨大呢？以及，我们该如何运用减法合成的手法模拟这些打击乐器的声音呢？

回想一下我们在上篇文章中讨论的绳子，不考虑其可以忽略不计的粗度，绳子只有一个维度——长度。虽然其他因素也会对绳子的震荡产生影响，比如说它的密度和张力，但在三维空间中，对于绳子来说最重要的属性只有长度。管状物也（大致）相同，其口径与材质会对其声音产生明显的影响，但是最重要的属性也只有长度一个。

现在想象一个圆形薄膜，其圆周的每一个点都被固定，并且被施加同等的力。鼓乐器的鼓面可以被类比为类似的圆膜，但我们在这里要将其当作另外一种振荡器来看待。像之前一样，为了简化这一假设，我们忽略鼓边匡上的木材和金属等因素，专注于鼓面这一振荡器本身。

这一圆膜和绳子的最大区别显而易见：与绳子不同，鼓面有两个维度：鼓面是一个平面，而不是一条线。你可能已经猜到鼓在被敲击、被拨动或者被吹动的时候的震荡方式和绳子相比会有很大区别。没错，振荡器的物理维度对于其声学属性来说至关重要。

让我们以一个圆形鼓乐器为例。与前文的绳子一样，它的鼓面圆周处被固定，震动的时候圆周无法自由移动。

现在想想看如果敲击这一鼓面的正中央，鼓面会产生什么样的震动。如果你的回答是和绳子一样上下往返运动的话，那么你就答对了。从侧面观察，圆膜的基频的震荡方式与绳子的震荡方式极其类似——参照图 1。这一震动类型被称作膜状物的 w01 震动模式。

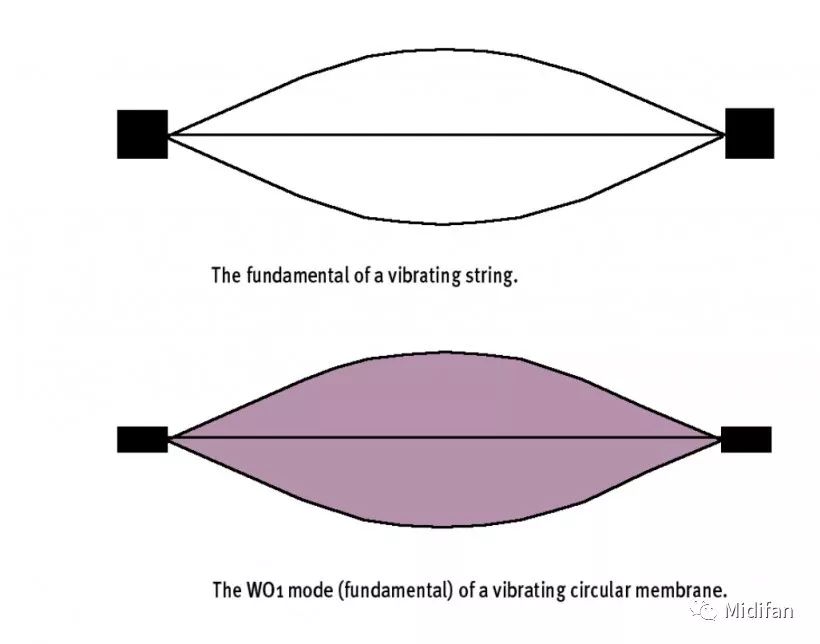
图 1：绳子的基频震动与圆形薄膜的 w01 震动模式 

（别担心，这次我不会和上一篇文章一样深入讨论这一震动的数学原理。因为膜状物的震动实在过于复杂，就算你是天体物理学家看到那些震荡模式的公式恐怕也会头疼。） 

因为你在敲击鼓面的正中央，所以你没办法用创建绳子的第二谐波的方法，将手指放在鼓面正中央，所以我们来看看鼓面震动的第三谐波。再回想一下绳子的震动方式，如果你将手指放在绳长三分之一的位置，可以生成频率正好为基频三倍的谐波。
       但如果用相同的方式，将手指放在鼓面半径三分之一的位置，那么你就找错位置了。与绳子的整数分之一的简单的「零点」关系不同，鼓面的零点要用一个叫做「贝塞尔函数」的极为复杂的公式计算。具体的计算方式我们不在本文讨论，你只需要知道，贝塞尔函数告诉我们鼓面的第一零点位于从鼓面中心到鼓边 42.6 的位置。另外，鼓面在进行这种震动（w02 震动模式）的时候产生的频率为基频的 2.296 倍。所以说，虽然膜状物的奇数泛音震动方式和绳子看起来相似，但其实两者的声学属性却大相径庭（见图 2）。

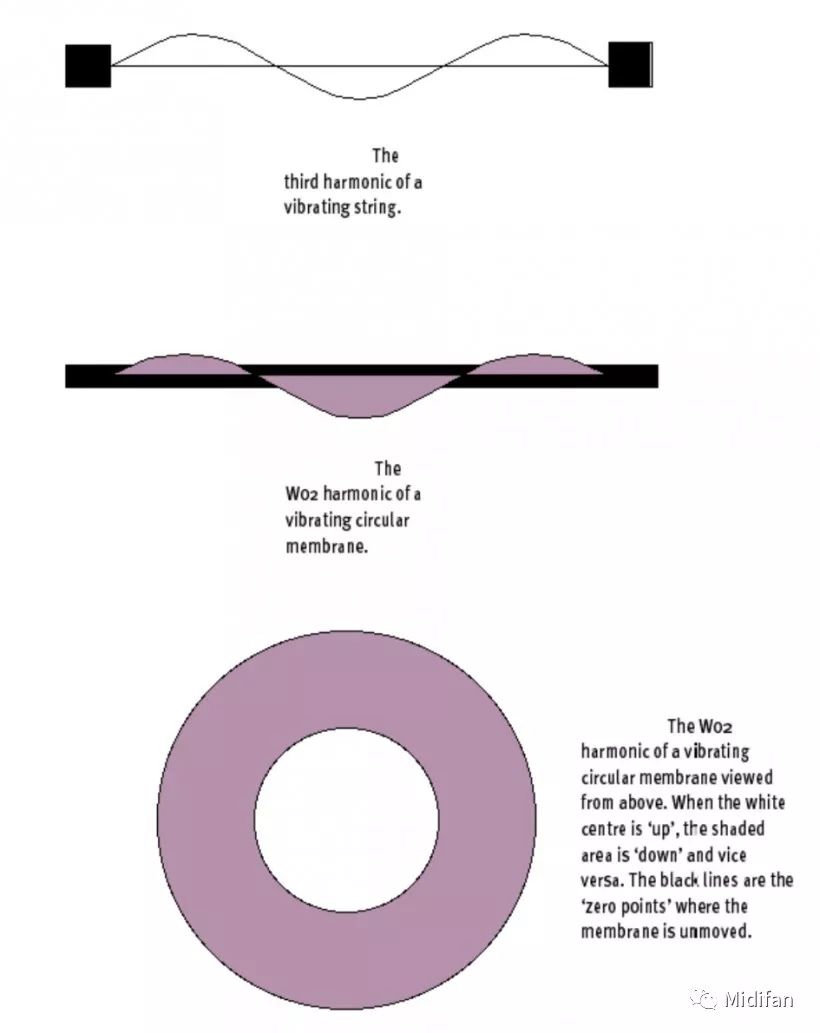
图 2：（由上到下依次为）绳子震荡产生的第三谐波；圆膜的 w02 震动模式；从上至下观察的圆膜 w02 震动，中央的白色部分位于平面「上方」，圆周处的阴影部分位于「下方」，以此往复震动。黑色的实线为震动的「零点」，薄膜的此处保持静止 

绳子的下一个奇数谐波——第五谐波将绳子平均分为五段，其频率为基频的五倍整。相对的，鼓面的下一个奇数谐波的零点位于圆心到圆周处 27.8 和 63.8 的位置，其频率为基频的 3.6 倍（图 3）。

图 3：从上至下观察的圆膜 w03 震动模式，白色部分位于平面「上方」，阴影部分位于「下方」，以此往复震动 

更为复杂的是，如果你敲击的不是鼓面的正中央，哪怕只是偏移一点点都会导致鼓面的震动方式变得完全不同，而且现实世界中，敲鼓的时候几乎每次都敲不到正中央。图 4 展示了鼓面的其他震动模式中的一小部分，以及震动产生的谐波与基础频率 f 的关系。

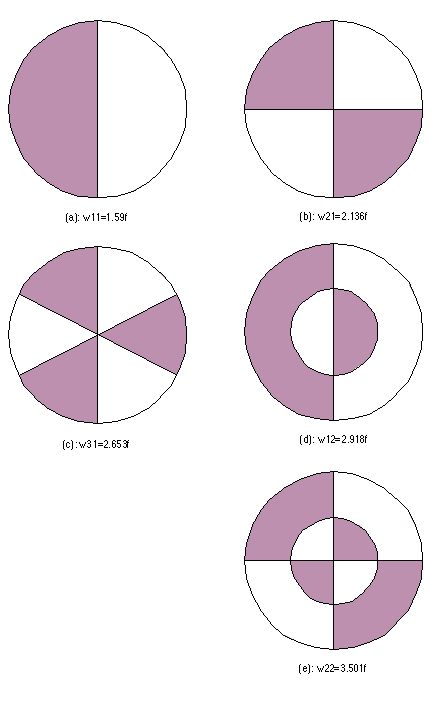
图 4：鼓面的其他几种震动模式 

和绳子一样，鼓面在震动的时候不只会生成一个单独的频率，而是会以多种模式同时震动。另外，这些震动的幅度与衰减速度全都不同。鼓乐器的音色因此而极其复杂，无法用简单的谐波振荡器生成的波形轻易模拟。

为了更明确地说明这一点，让我们把锯齿波的前四个谐波与鼓被敲击时产生的波形的前几个谐波分布对比来看（见图 5）。

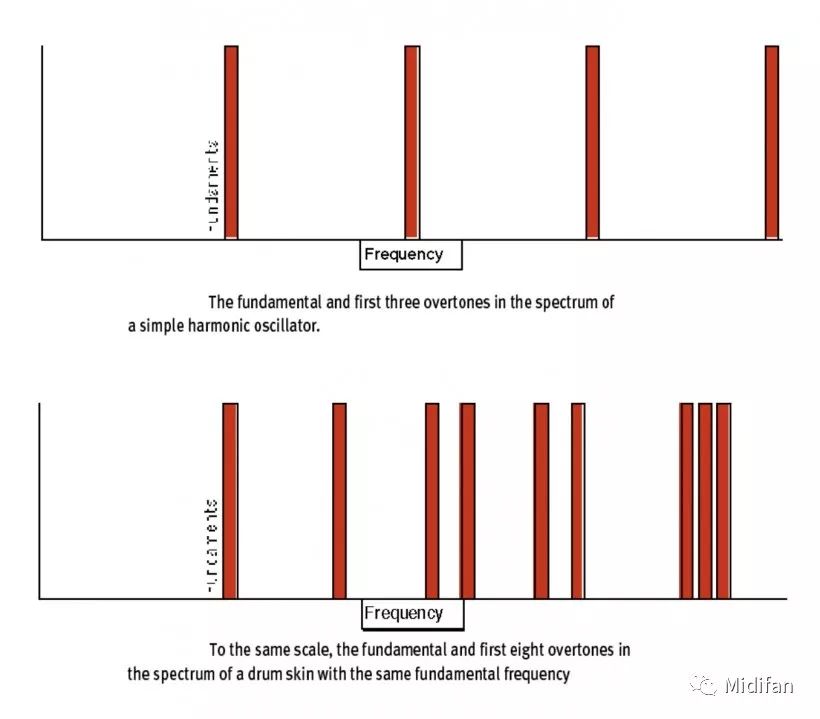
图 5：（上）简单谐波振荡器的基频与前三个泛音；（下）同样基频的鼓面及其前八个泛音 

不难看到，简单谐波振荡器产生的谐波在频谱上规则分布，而鼓面震动产生的谐波数量更多，并且以一种不规则的形态分布。正是因此鼓乐器的音色具备「无调性」的特征，我们在聆听鼓音色的时候很难感知到一个简单的音高或者声调。如果你继续观察鼓面的高频谐波，你就会发现其在频率越高的位置谐波的数量就越多，并且分布越紧凑。随便观察一个鼓面震动的频谱，即便是基频只有 100Hz 的鼓音色，它的谐波分布也能一直延展至人类听觉极限 20kHz 甚至更高的位置。

然而这还仅仅只是理想状态下的情况，真实世界中的各种因素会让鼓音色变得更为复杂得多。比如说，无论你将鼓调整得多么精准，鼓面的不同位置的张力总是会有一些细微的差别，其震动模式也会因此发生变化，几乎无法准确计算。另外，每个鼓手都知道，敲鼓的时候用力越大鼓的音高就越高，也就是说鼓面的位移幅度还会对鼓的基频产生影响...

我的建议是：虽然鼓的发声原理看上去简单，但实际情况要复杂得多的多，还是不要试图精确分析它为好。有研究者花了几十年时间构建出来了庞大、复杂的膜状物震动数学模型，但即使是运用了这些复杂算法的 DSP 设备产生的鼓音色与「真实」的鼓乐器比起来效果也只能算差强人意。所以说我们的模拟合成器就只能模拟 70 年代的小号和提琴音色，在鼓音色面前只能缴械投降了吗？然而答案并非如此...

让我们把鼓音色放在模拟合成器的环境中思考。如果我们要合成一个与鼓的声音类似的音色，我们需要一个类似前文描述的分布非常密集的谐波，并且需要保证这些谐波之间没有传统的和声关联。幸运的是，大多数合成器都有一个具备类似功能的模块——「噪声发生器（noise generator）」可以同时产生所有的音频频率，利用这一特性我们可以取得普通振荡器难以产生的波形，为模拟「鼓」音色提供基础。实际上，许多 90 年代经典的打击乐音色——Roland CR78, CR5000, TR808 等等鼓机的声音都是使用经过滤波的噪声合成的。

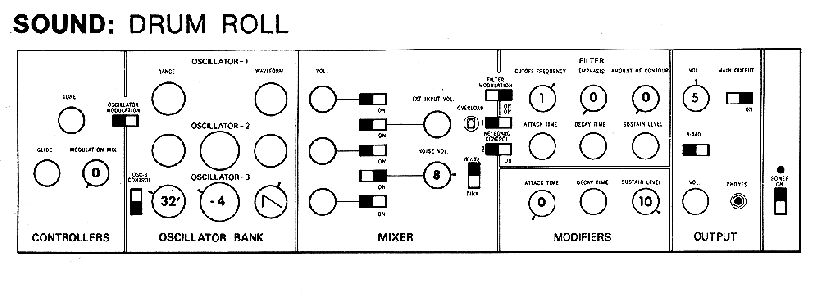
图 6：使用 Minimoog 合成器合成的简单鼓音色 

但除了鼓之外其他的打击乐器又该怎么办呢？其实包括钹和锣在内的这些乐器在许多方面都和鼓非常类似。虽然这些乐器的质地是坚固的，并且边缘没有被固定，和柔性、被拉伸的鼓面不同，但它们的震荡模式的数学原理和膜状物其实是共通的。即使是铃铛这类拥有一定体积，看上去是三维的乐器也其实被描述为二维振荡器更加合适，因为它们可以被简化为是由弯曲、折叠的平面构成的。

然而，金属打击乐器与鼓乐器在物理构造上的区别导致了只用噪声发生器合成出的铃铛与锣声等音色效果并不是很理想。这也就是类似图 6 中的 Minimoog 这类基础合成器的短板。然而如果观察 ARP Odyssey 或者 ARP 2600 这些复杂合成器的音色表，你却能找到许多「金属」的音色。这是因为这些合成器都具备「环形调制器（ring modulator）」模块。环形调制器是一个可以生成大量密集、不和谐泛音的电路，其泛音特征与金属薄片类似。利用这一特性，再结合滤波器与包络的调制，就能合成出简单谐波振荡器难以生成的打击乐音色。