为什么要用稀疏自编码器

什么是自编码

简单的自编码是一种三层神经网络模型，包含了数据输入层、隐藏层、输出重构层，同时它是一种无监督学习模型。在有监督的神经网络中，我们的每个训练样本是（X，y），然后y一般是我们人工标注的数据。比如我们用于手写的字体分类，那么y的取值就是0~9之间数值，最后神经网络设计的时候，网络的输出层是一个10个神经元的网络模型（比如网络输出是（0，0，1，0，0，0，0，0，0，0），那么就表示该样本标签为2）。然而自编码是一种无监督学习模型，我们训练数据本来是没有标签的，那么自编码是这样干的，它令每个样本的标签为y=x，也就是每个样本的数据x的标签也是x。自编码就相当于自己生成标签，而且标签是样本数据本身。

三层自编码神经网络模型如下：

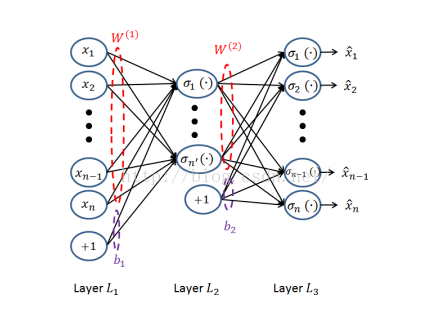
自编码网络包含两个过程：

（1）从输入层-》隐藏层的原始数据X的编码过程：

（2）从隐藏层-》输出层的解码过程：

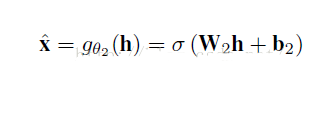
那么数据X的重构误差损失函数就是：

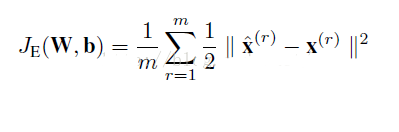
其中M是训练样本的个数。

因此等我们训练完网络后，当我们随便输入一个测试样本数据X‘，那么自编码网络将对X‘先进行隐藏层的编码，然后再从隐藏-》输出完成解码，重构出X’。隐藏层可以看成是原始数据x的另外一种特征表达。

这个时候就会有人问自编码有什么作用，训练一个神经网络模型，让它输入是x，然后输出也近似x，有毛用？其实自编码可以实现类似于PCA等数据降维、数据压缩的特性。从上面自编码的网络结构图，如果输入层神经云的个数n小于隐层神经元个数m，那么我们就相当于把数据从n维降到了m维；然后我们利用这m维的特征向量，进行重构原始的数据。这个跟PCA降维一模一样，只不过PCA是通过求解特征向量，进行降维，是一种线性的降维方式，而自编码是一种非线性降维。

当然自编码隐藏层可以比输入层的神经元个数还多，然后我们可以在神经网络的损失函数构造上，加入正则化约束项进行稀疏约束，这个时候就演化成了稀疏自编码了，因此我们接着就说说稀疏自编码。

为什么要用稀疏自编码器

对于没有带类别标签的数据，由于为其增加类别标记是一个非常麻烦的过程，因此我们希望机器能够自己学习到样本中的一些重要特征。通过对隐藏层施加一些限制，能够使得它在恶劣的环境下学习到能最好表达样本的特征，并能有效地对样本进行降维。这种限制可以是对隐藏层稀疏性的限制。

如果给定一个神经网络，我们假设其输出与输入是相同的，然后训练调整其参数，得到每一层中的权重。自然地，我们就得到了输入的几种不同表示（每一层代表一种表示），这些表示就是特征。自动编码器就是一种尽可能复现输入信号的神经网络。为了实现这种复现，自动编码器就必须捕捉可以代表输入数据的最重要的因素，就像PCA那样，找到可以代表原信息的主要成分。

当然，我们还可以继续加上一些约束条件得到新的Deep Learning方法，如：如果在AutoEncoder的基础上加上L1的Regularity限制（L1主要是约束隐含层中的节点中大部分都要为0，只有少数不为0，这就是Sparse名字的来源），我们就可以得到Sparse AutoEncoder法。

之所以要将隐含层稀疏化，是由于，如果隐藏神经元的数量较大（可能比输入像素的个数还要多），不稀疏化我们无法得到输入的压缩表示。具体来说，如果我们给隐藏神经元加入稀疏性限制，那么自编码神经网络即使在隐藏神经元数量较多的情况下仍然可以发现输入数据中一些有趣的结构。

2. 稀疏自编码器的解释

稀疏性可以被简单地解释如下。如果当神经元的输出接近于1的时候我们认为它被激活，而输出接近于0的时候认为它被抑制，那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里我们假设的神经元的激活函数是sigmoid函数。如果你使用tanh作为激活函数的话，当神经元输出为-1的时候，我们认为神经元是被抑制的。

3. 模型

5

我们的目标是，使得hw，b（x）=xhw，b（x）=x。并且通过隐含层，得到输入的压缩表示。

在神经网络里面，我们得到的隐含层输出用a表示。在这里，我们将其转换一下概念。a（2）jaj（2）是隐含层第j个单元的输出。a（2）j（x（i））aj（2）（x（i））表示在给定输入为 x 情况下，自编码神经网络隐藏神经元 j 的激活度。 进一步，让

ρˆ=1m∑mi=1a（2）j（x（i））ρ^=1m∑i=1maj（2）（x（i））

表示隐藏神经元 j 的平均活跃度（在训练集上取平均）。我们可以近似的加入一条限制。

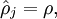
其中， ρρ 是稀疏性参数，通常是一个接近于0的较小的值（比如 ρρ= 0.05 ）。换句话说，我们想要让隐藏神经元 ρˆρ^的平均活跃度接近0.05。为了满足这一条件，隐藏神经元的活跃度必须接近于0。

为了实现这一限制，我们将会在我们的优化目标函数中加入一个额外的惩罚因子，而这一惩罚因子将惩罚那些ρˆρ^ 和 ρρ 有显著不同的情况从而使得隐藏神经元的平均活跃度保持在较小范围内。惩罚因子的具体形式有很多种合理的选择，我们将会选择以下这一种（KL散度）：

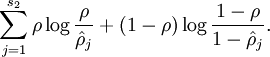
其中为了方便书写：

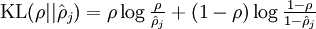
这样，神经网络整体代价函数就可以表示为：

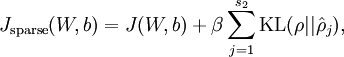
然后我们基于此再推导一次神经网络的反向传播算法。

最后我们得到，原本的神经网络误差项：

变成：

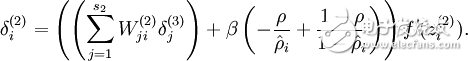
接下来就是训练神经网络，直到收敛了。到最后，我们可以得到输入层到隐含层的权重，利用这我们可以知道我们学习到了什么。具体可参考可视化自编码器训练结果