稀疏自编码器及TensorFlow实现详解

自编码器（AutoEncoder）顾名思义，就是可以用自身的高阶特征编码自己。自编码器实际上也是一种神经网络，它的输入和输入的维度是一样的。借助稀疏编码的思想，目标是使用稀疏的一些高阶特征重新组合来重构自己。

早年在关于稀疏编码（Sparse Coding）的研究中，通过对大量黑白风景照片提取16*16的图像碎片分析，研究发现几乎所有的图像碎片都可以由64种正交的边组合得到，并且组合出一张图像碎片需要的边的数量是很少的，也就是稀疏的。声音也有同样的情况，大量未标注的音频中可以得到20种基本结构，绝大多数声音都可以由这些基本的结构线性组合得到。这就是特征的稀疏表达，通过少量的基本特征组合、拼装得到更高层抽象的特征。

Sparsity 是当今机器学习领域中的一个重要话题。

Sparsity 的最重要的“客户”大概要属 high dimensional data 了吧。现在的机器学习问题中，具有非常高维度的数据随处可见。例如，在文档或图片分类中常用的 bag of words 模型里，如果词典的大小是一百万，那么每个文档将由一百万维的向量来表示。高维度带来的的一个问题就是计算量：在一百万维的空间中，即使计算向量的内积这样的基本操作也会是非常费力的。不过，如果向量是稀疏的的话（事实上在 bag of words 模型中文档向量通常都是非常稀疏的），例如两个向量分别只有L1 和 L2 个非零元素，那么计算内积可以只使用min（L1，L2） 次乘法完成。因此稀疏性对于解决高维度数据的计算量问题是非常有效的。

稀疏自编码器及TensorFlow实现详解

稀疏自编码器（又称稀疏自动编码机）中，重构误差中添加了一个稀疏惩罚，用来限定任何时刻的隐藏层中并不是所有单元都被激活。如果 m 是输入模式的总数，那么可以定义一个参数 ρ_hat，用来表示每个隐藏层单元的行为（平均激活多少次）。基本的想法是让约束值 ρ_hat 等于稀疏参数 ρ。具体实现时在原始损失函数中增加表示稀疏性的正则项，损失函数如下：

如果 ρ_hat 偏离 ρ，那么正则项将惩罚网络，一个常规的实现方法是衡量 ρ 和 ρ_hat 之间的 Kullback-Leiber（KL） 散度。

准备工作

在开始之前，先来看一下 KL 散度 DKL 的概念，它是衡量两个分布之间差异的非对称度量，本节中，两个分布是 ρ 和 ρ_hat。当 ρ 和 ρ_hat 相等时，KL 散度是零，否则会随着两者差异的增大而单调增加，KL 散度的数学表达式如下：

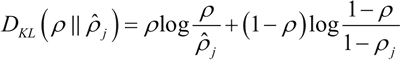
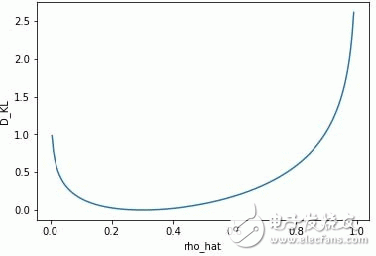
下面是 ρ=0.3 时的 KL 的散度 DKL 的变化图，从图中可以看到，当 ρ_hat=0.3时，DKL=0；而在 0.3 两侧都会单调递增：

具体做法

导入必要的模块：

从 TensorFlow 示例加载 MNIST 数据集：

定义 SparseAutoEncoder 类，除了引入 KL 散度损失之外，它与前面的自动编码机类非常相似：

将 KL 约束条件添加到损失函数中，如下所示：

其中，alpha 是稀疏约束的权重。该类的完整代码如下所示：

声明 SparseAutoEncoder 类的一个对象，调用 fit（） 训练，然后计算重构的图像：

重构损失均方误差随网络学习的变化图：

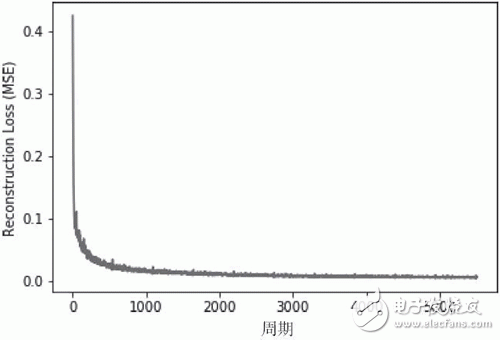
查看重构的图像：

结果如下：

解读分析

必须注意到，稀疏自编码器的主要代码与标准自动编码机完全相同，稀疏自编码器只有一个主要变化——增加了KL散度损失以确保隐藏（瓶颈）层的稀疏性。如果将两者的重构结果进行比较，则可以看到即使隐藏层中的单元数量相同，稀疏自动编码机也比标准自动编码机好很多：

在 MNIST 数据集上，标准自动编码机训练后的重构损失是 0.022，而稀疏自编码器是 0.006，由此可见稀疏自编码器对数据的内在表示学习得更好一些。