

RC充电电路曲线及电表案例
描述
当电压源施加到RC电路时,电容器C通过电阻充电,R
所有电气或电子电路或系统都受到某种形式的“时间 - 当首先对信号或电压施加连续,(DC)或交流(AC)时,它在输入和输出之间延迟。
这种延迟通常被称为时间延迟或时间常数电路,它是首次施加阶跃电压或信号时电路的时间响应。任何电子电路或系统的合成时间常数将主要取决于与其电容或电感相连的无功分量,并且是对单位的响应时间的测量,Tau -τ
当增加的直流电压施加到放电电容器时,电容器吸收充电电流并“充电”,当电压降低时,电容器以相反方向放电。由于电容器能够存储电能,因此它们就像小电池一样,可以根据需要存储或释放能量。
电容器极板上的电荷如下: Q = CV 。电容器能量的充电(存储)和放电(释放)永远不会立即发生,但需要一定的时间才能使电容器充电或放电到其最大电源值的一定百分比内所需的时间被称为时间常数(τ)。
如果电阻与形成RC电路的电容串联,电容会逐渐充电电阻器直到电容器两端的电压达到电源电压。时间也称为瞬态响应,电容器完全充电所需的时间约等于5时间常数或 5T 。
此瞬态响应时间 T ,以 τ = R x C 为单位,以秒为单位,其中 R 是值以欧姆为单位的电阻和 C 是以法拉为单位的电容值。这就形成了RC充电电路的基础, 5T 也可以被认为是“5 x RC”。
RC充电电路
下图显示了一个与电阻串联的电容( C ),( R )形成RC充电电路通过机械开关连接直流电池电源( Vs )。当开关闭合时,电容器将逐渐通过电阻器充电,直到其两端的电压达到电池的电源电压。电容器充电的方式也如下所示。
RC充电电路

我们在上面假设,电容 C 完全“放电”且开关(S)完全打开。这些是电路的初始条件,然后 t = 0 , i = 0 和 q = 0 。当开关闭合时,时间从 t = 0 开始,电流开始通过电阻器流入电容器。
由于电容器两端的初始电压为零,( Vc = 0 )电容似乎是外部电路的短路,最大电流仅通过电阻 R 限制。然后通过使用基尔霍夫电压定律(KVL),电路周围的电压降为:
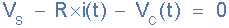
现在流经电路的电流称为充电电流,通过使用欧姆定律得出: i = Vs / R 。
RC充电电路曲线
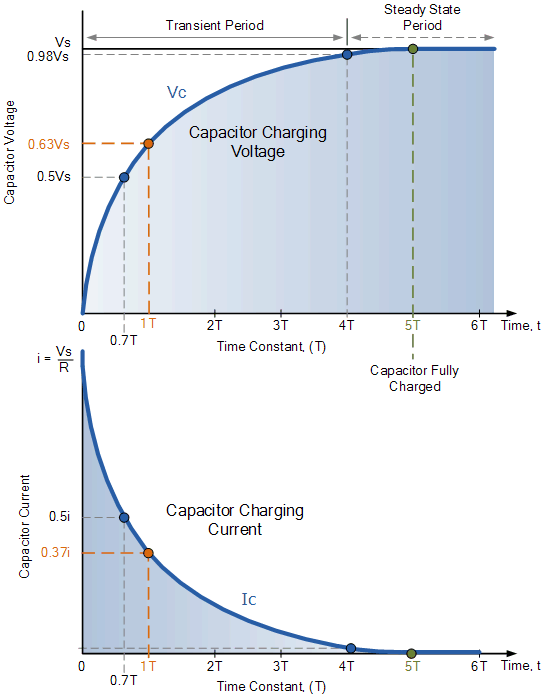
电容现在开始充电,如图所示,RC充电曲线的上升在开始时更陡,因为充电速率在开始时最快,然后随着电容器的变化而逐渐减小以较慢的速率充电。
随着电容器充电,电路板上的电位差逐渐增大,电容器充电的实际时间达到 63%其最大可能电压,在我们的曲线 0.63Vs 中称为一个时间常数,( T )。
此 0.63Vs 电压点的缩写为 1T ,(一个时间常数)。
电容继续充电, Vs 之间的电压差并且 Vc 减小,因此电路电流 i 。然后在最终条件下,当电容器被称为完全充电时,大于五个时间常数( 5T ), t = ∞, i = 0 , q = Q = CV 。然后在无穷大时,电流减小到零,电容就像一个开路状态,因此,电压降完全在电容上。
所以在数学上我们可以说电容器充电所需的时间到一个时间常数,( 1T )给出如下:
RC时间常数,Tau

此RC时间常数仅指定一个充电速率,其中 R 在Ω中, C 以法拉为单位。
由于电压 V 与电容器上的电荷有关,公式为 Vc = Q / C ,电压两端的电压值( Vc )在充电期间的任何时刻都给出如下:
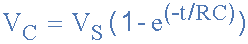
其中:
Vc 是电容两端的电压
Vs 是电源电压
t 是自施加电源电压以来经过的时间
RC 是RC充电电路的时间常数
经过相当于4个时间常数的周期后,( 4T )此RC充电电路中的电容几乎完全充电,电容两端的电压现在约为其最大值的98%, 0.98Vs 。电容达到 4T 点所需的时间称为瞬态周期。
经过 5T
后
span>电容器现在已充满电,电容器两端的电压( Vc )等于电源电压( Vs )。当电容器完全充电时,电路中不再有电流流过。此 5T 点之后的时间段称为稳态周期。
然后我们可以在下表中显示百分比电压和电流值对于给定时间常数的RC充电电路中的电容器。
RC充电表

注意作为收费曲线RC充电电路是指数级的,由于存储在电容器中的能量,电容器实际上永远不会变为100%完全充电。因此,出于所有实际目的,在五个时间常数之后,电容器被认为是完全充电的。
当电容器两端的电压 Vc 随时间变化时,并且是不同的值每次常数达到 5T 时,我们可以计算出任何给定点的电容器电压值 Vc 。
RC充电电路示例No1
计算以下电路的RC时间常数τ。
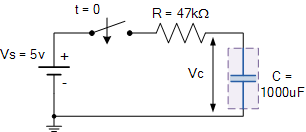
时间常数τ使用公式 T = R x C 以秒为单位。
因此时间常数τ是给定为: T = R x C = 47k x 1000uF = 47秒
a)在0.7时间常数下,电容两端的电压是多少? ?
在0.7时间常数( 0.7T )Vc = 0.5Vs。因此,Vc = 0.5 x 5V = 2.5V
b)电压值是多少?电容在1时间常数?
在1时间常数( 1T )Vc = 0.63Vs。因此,Vc = 0.63 x 5V = 3.15V
c)需要多长时间“完全充电“电容器?
电容器将以5个时间常数充满电。
1个时间常数( 1T )= 47秒,(从上面)。因此, 5T = 5 x 47 = 235秒
d)100秒后电容器两端的电压?
电压公式为 Vc = V(1-e ( - t / RC)) 所以这变成: Vc = 5(1 - e ( - 100/47))
其中:V = 5伏, t = 100秒,RC =从上面47秒。
因此, Vc = 5(1 - e ( - 100/47)) = 5(1 - e -2.1277 )= 5(1 - 0.1191)= 4.4伏
我们见过电容器上的电荷由下式给出: Q = CV 并且当电压首先施加到电容器的极板上时,它以由其时间常数τ。
在下一个教程中,我们将检查放电电容器的电流 - 电压关系,并在电容器板短接在一起时查看与之相关的曲线。
-
AA电池充电表2022-08-08 0
-
关于RC充电电路的一些方法总结!2020-09-08 0
-
RC充电电路图2009-05-08 2023
-
rc串联电路的幅频特性曲线介绍2018-02-10 81902
-
RC放电电路曲线定义案例2019-06-27 26191
-
RC积分器电路公式及增长案例曲线摘要2019-06-27 32135
-
一文详解RC充电电路计算方法2022-05-17 18813
-
你需要了解的RC放电电路2023-05-22 1793
-
RC充电电路的计算及仿真2023-07-12 3202
-
RC充电电路中要多久才能把电容的电充满?2023-11-02 1201
-
RC时间常数的意思是什么?怎么算RC时间常数?RC时间常数的测量?2023-11-20 14058
-
RC滞后和RC延迟是同一种电路吗?2023-11-20 798
-
RC电路是什么?为什么充放电慢?2023-11-20 2093
-
rc复位电路的电阻作用2023-12-14 1773
-
电池充电特性曲线2023-12-22 3067
全部0条评论

快来发表一下你的评论吧 !

