感应电抗相量图和电频率案例

线圈的感应电抗取决于施加电压的频率，因为电抗与频率成正比

到目前为止，我们已经研究了连接到直流电源的电感的行为，并希望通过现在我们知道，当在电感上施加直流电压时，通过它的电流的增长不是瞬间的，而是由电感自感应或反电动势值决定的。

我们也看到了电感器电流继续上升，直到它在五个时间常数后达到其最大稳态条件。流过电感线圈的最大电流仅受线圈绕组的电阻部分的限制，单位为欧姆，正如我们从欧姆定律所知，这是由电压与电流之比决定的， V / R 。

当在电感器上施加交流或交流电压时，通过它的电流与施加的直流电压的行为非常不同。正弦电源的影响在电压和电流波形之间产生相位差。现在在交流电路中，电流流过线圈绕组的反对不仅取决于线圈的电感，还取决于交流波形的频率。

对流过线圈的电流的反对交流电路由电路的交流电阻决定，通常称为阻抗（Z）。但是电阻总是与直流电路相关联，所以为了区分直流电阻和交流电阻，通常使用电抗。

就像电阻一样，电抗值也用欧姆测量但是给出符号 X ，（大写字母“X”），以区别于纯电阻值。

由于我们感兴趣的组件是电感器，因此，电感器的电抗称为“感应电抗”。换句话说，当在交流电路中使用时，电感器的电阻称为感应电抗。

感应电抗，其符号为 X L ，是交流电路中与电流变化相反的特性。在我们关于交流电路中电容器的教程中，我们看到在纯电容电路中，电流 I C “LEADS”电压为90 o 。在纯电感的交流电路中，恰恰相反，电流 I L “LAGS”施加的电压为90 o 或（π） / 2 rads）。

交流电感电路

在上面的纯电感电路中，电感直接连接在交流电源电压上。随着电源电压随频率的增加而减小，相对于这种变化，自感应反电动势也会在线圈中增加和减少。

我们知道这种自感电动势与电磁场成正比。通过线圈的电流变化率最大，因为电源电压从其正半周期到负半周期交叉，反之亦然，在点0 o 和180 o 沿着正弦波。

因此，当AC正弦波以其最大或最小峰值电压电平交叉时，电压的最小变化率发生。在周期中的这些位置，最大或最小电流流过电感电路，如下所示。

交流电感相量图

这些电压和电流波形表明，对于纯电感电路，电流滞后电压90 o 。同样，我们也可以说电压使电流超过90 o 。无论哪种方式，一般表达式是当前滞后，如矢量图所示。这里，电流矢量和电压矢量显示为90° o 。 电流滞后于电压。

我们也可以将此语句写为， V L = 0 o 和 I L = - 90 o 关于电压， V L 。如果电压波形被归类为正弦波，则电流 I L 可归类为负余弦，我们可以定义任意点的电流值。时间为：

其中：ω以弧度/秒为单位 t 以秒为单位。

由于在纯电感电路中电流始终滞后电压90° o ，我们可以通过了解电压的相位来找到电流的相位，反之亦然。因此，如果我们知道 V L 的值，那么 I L 必须滞后90 o 。同样，如果我们知道 I L 的值，那么 V L 因此必须由90 o引导。然后，电感电路中的电压与电流之比将产生一个方程，该方程定义了线圈的感应电抗，X L。

感应电抗

我们可以将感应电抗的上述等式重写为更熟悉的形式，使用普通频率以弧度为单位提供而不是角频率，ω，其值为：

其中： ƒ是频率， L 是线圈的电感，2πƒ=ω。

从上面的感应电抗方程，可以看出，如果频率或电感中的任何一个增加，则总感应电抗值也将增加。当频率接近无穷大时，电感器电抗也会增加到无穷大，就像开路一样。

然而，当频率接近零或DC时，电感器电抗会降低到零，就像短路一样。这意味着感应电抗与频率“成比例”。

换句话说，感抗随频率增加，导致 X L 小低频和 X L 在高频时为高电平，如下图所示：

频率感应电抗

<表类=“table2”>

斜率表示电感的“感应电抗”增加随着它的供电频率增加。

因此感应电抗与频率给定成正比:( X L αƒ）

然后我们可以看到在DC处电感器具有零电抗（短路），在高频时电感器具有无功电抗（开路）。

感应电抗实例No1

电感线圈150mH，零电阻连接在100V，50Hz电源上。计算线圈的感抗和流过它的电流。

通过LR系列电路供电

到目前为止，我们已经考虑过纯电感线圈，但不可能有纯电感，因为所有线圈，继电器或螺线管都会有一定的电阻，无论线圈匝数有多小。正在使用的电线。然后我们可以将简单线圈视为与电感串联的电阻。

在包含电感， L 和电阻的交流电路中， R 电压， V 将是两个分量电压的相量和， V R 和 V L 。这意味着流过线圈的电流仍将滞后于电压，但是小于90 o 的量取决于 V R 的值和 V L 。

电压和电流之间的新相角被称为电路的相角，并给出了希腊符号phi，Φ。

为了能够产生电压和电流之间关系的矢量图，必须找到参考或公共分量。在串联的R-L电路中，当相同的电流流过每个元件时，电流是常见的。该参考量的矢量通常从左到右水平绘制。

从我们关于电阻器和电容器的教程中我们知道电阻式交流电路中的电流和电压都是“同相”的，因此向量， V R 在当前或参考线上按比例绘制。

我们也从上面知道，当前“滞后”了纯电感电路中的电压，因此矢量， V L 在电流基准前面绘制90 o ，并且与 V R ，如下所示。

LR系列交流电路

在上面的矢量图中可以看到行OB 表示电流参考线，线 OA 是电阻元件的电压，并且与电流同相。线 OC 表示电流前的感应电压为90 o ，因此可以看出电流滞后电压90 o 。线 OD 给出了电路上的结果或电源电压。电压三角形来自毕达哥拉斯定理，并给出如下：

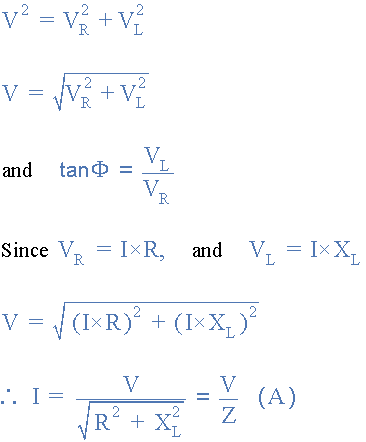
在直流电路中，比率为电压到电流称为电阻。然而，在AC电路中，该比率被称为阻抗，Z，其单位再次以欧姆为单位。阻抗是包含电阻和感抗的“交流电路”中的电流总阻抗。

如果我们将电压三角形的边上方除以电流，则得到另一个三角形，其边代表线圈的电阻，电抗和阻抗。这个新三角被称为“阻抗三角”

阻抗三角

感应电抗示例No2

电磁线圈的电阻为30欧姆，电感为0.5H。如果流过线圈的电流是4安培。计算，

a）频率为50Hz时的电源电压。

b）电压和电流之间的相角。

电源交流电感的三角形

我们可以将另一种类型的三角形配置用于电感电路，即“功率三角形”。电感电路中的功率称为无功功率或伏特无功电阻，符号Var，以伏安为单位测量。在RL系列交流电路中，电流滞后电源电压角度Φ o 。

在纯电感交流电路中，电流将与电源电压完全相差90° o 。因此，线圈消耗的总无功功率将等于零，因为所产生的自感应电动势功率抵消了任何消耗的功率。换句话说，纯电感器在一个完整周期结束时消耗的净功率（瓦特）为零，因为能量都来自电源并返回到电源。

无功功率，（ Q ）线圈可以给出： I 2 xX L （类似于I 2 直流电路中的R）。然后，交流电路中功率三角形的三个边由视在功率（ S ），实际功率（ P ）和无功功率（ Q ）如图所示。

Power Triangle

请注意由于绕组的电阻产生阻抗， Z ，实际的电感或线圈将消耗功率，单位为瓦特。