LR系列电路定律和瞬态曲线案例及功率

所有线圈，电感器，扼流圈和变压器在其周围产生磁场，包括与电阻串联的电感，形成LR系列电路

本节的第一篇关于电感器的教程，我们简要地看了一下电感的时间常数，说明流经电感的电流不会瞬间改变，但会以恒定的速率增加，这是由电感中的自感电动势决定的。

其他换句话说，电路中的电感器与电流的流动相反，（i）通过它。虽然这是完全正确的，但我们在教程中假设它是一个理想的电感器，没有与其线圈绕组相关的电阻或电容。

然而，在现实世界中“ALL”线圈是否它们是是扼流圈，螺线管，继电器或任何伤口组件总是会有一定的阻力，无论多小。这是因为实际线圈匝数用于使其使用具有电阻值的铜线。

然后，出于现实目的，我们可以将我们的简单线圈视为“电感”，L与“电阻”串联，R。换句话说，形成LR系列电路

ALR系列电路基本上由一个电感电感器L组成，L与一个电阻器串联。电阻“R”是构成电感线圈的导线匝数或环路的直流电阻值。考虑下面的LR系列电路。

LR系列电路

以上 LR串联电路连接在恒压源（电池）和开关之间。假设开关S打开直到它在时间t = 0闭合，然后保持永久闭合，产生“阶跃响应”型电压输入。电流，i开始流过电路，但不会迅速上升到其最大值Imax，由V / R（欧姆定律）的比值决定。

这个限制因素是由于存在由于磁通量的增长，电感器内的自感电动势（Lenz定律）。经过一段时间后，电压源抵消了自感电动势的影响，电流变得恒定，感应电流和磁场减小到零。

我们可以使用基尔霍夫电压定律，（ KVL ）定义电路周围存在的各个电压降，然后希望用它来表示电流的流动。

基尔霍夫电压定律（KVL）给出了：

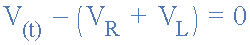
电阻上的电压降 R I * R （欧姆法）。

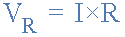
电感器上的电压降 L 现在是我们熟悉的表达式 L （di / dt）

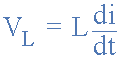
然后个别电压的最终表达式在LR周围下降串联电路可以给出：

我们可以看到电阻两端的电压降取决于电流， i ，而电感上的电压降取决于电流的变化率， di / dt 。当电流等于零时，（ i = 0 ）在时间 t = 0 时，上述表达式（也是一阶微分方程）可以被重写为给出在任何时刻的电流值为：

LR系列电路中电流的表达式

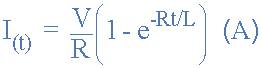
其中：

V 以伏特为单位

R 以欧姆为单位

L 在Henries中

t 是秒。

e 是基础自然对数= 2.71828

LR系列电路的时间常数，（τ）给出为L / R和其中V / R表示五个时间常数值后的最终稳态电流值。一旦电流达到5τ时的最大稳态值，线圈的电感就会减小到零，更像是一个短路，并有效地将其从电路中移除。

因此流过线圈的电流仅受线圈绕组的欧姆电阻元件的限制。表示电路电压/时间特性的电流增长的图形表示可以表示为。

LR系列电路的瞬态曲线

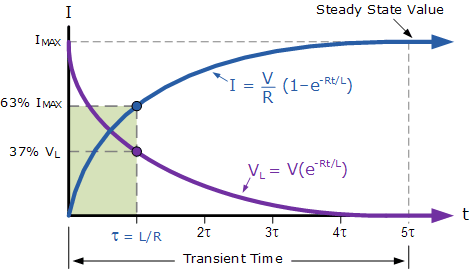
由于电阻上的电压降， V R 等于 I * R （欧姆定律），它将具有与当前相同的指数增长和形状。但是，电感上的电压降 V L 的值等于： Ve （ - Rt / L） 。然后，电感两端的电压 V L 的初始值将等于 t = 0 时的电池电压或开关为首先闭合，然后如上面的曲线所示，指数衰减到零。

LR系列电路中流过的电流达到最大稳态值所需的时间相当于大约<5>时间常数或5τ。此时间常数τ，以τ = L / R （以秒为单位）测量，其中 R 为值电阻的单位为欧姆， L 是亨利斯电感的值。这就形成了RL充电电路的基础 5 τ也可以被认为是“ 5 *（L / R）”或电路的瞬态时间

任何电感电路的瞬态时间由电感和电阻之间的关系决定。例如，对于固定值电阻，电感越大，瞬态时间越慢，因此LR串联电路的时间常数越长。同样，对于固定值电感，电阻值越小，瞬态时间越长。

然而，对于固定值电感，通过增加电阻值，电路的瞬态时间和时间常数变短。这是因为随着电阻增加，电路变得越来越具有电阻性，因为与电阻相比，电感值变得可以忽略不计。如果电阻值与电感相比增加得足够大，则瞬态时间将有效地降低到几乎为零。

LR系列电路示例No1

具有电感的线圈将40mH和2Ω的电阻连接在一起以形成LR串联电路。如果它们连接到20V直流电源。

a）。电流的最终稳态值是什么。

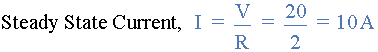
b）RL系列电路的时间常数是什么。

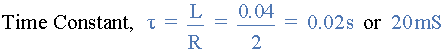
c）RL系列电路的瞬态时间是什么。

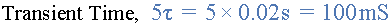
d）10ms后诱导电动势的值是多少。

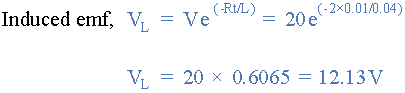
e）开关关闭后电路电流值的一个时间常数是什么。

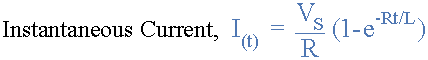
电路的时间常数，τ在问题b）中计算为 20ms的 。那么此时的电路电流如下：

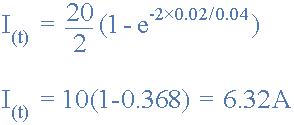
您可能已经注意到问题的答案（e）在一个时间常数下给出6.32安培的值，等于我们计算的10安培的最终稳态电流值的63.2％（a） 。该值为63.2％或0.632xI MAX 也与上面所示的瞬态曲线相对应。

LR系列电路中的功率

然后从上面看，电压源向电路供电的瞬时速率如下：

瞬时速率电阻以热量的形式消耗的功率为：

能量的速率以磁势能量的形式存储在电感中的情况如下：

然后我们可以找到总数RL系列电路中的功率乘以 i ，因此：

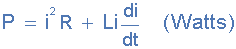
第一个 I 2 R 项表示电阻器在加热时消耗的功率，第二项表示电感器吸收的功率，即其磁能。