异或门等效电路教程及功能

异或逻辑功能是一种非常有用的电路，可用于许多不同类型的计算电路

在之前的教程中，我们看到通过使用三个主要门，在AND门，OR门和NOT门之间，我们可以构建许多其他类型的逻辑门功能，例如NAND门和NOR门或我们可以想象的任何其他类型的数字逻辑功能。

但是还有另外两种类型的数字逻辑门虽然它们本身不是基本门，因为它们是通过将其他逻辑门组合在一起构建的，但它们的输出布尔函数非常重要，可以被视为完整的逻辑门。这两个“混合”逻辑门称为异或（Ex-OR）门，它与异或（Ex-NOR）门互为补充。

以前，我们看到对于2输入 OR 门，如果A =“1”，ORB =“1”，或两者兼而有之A + B =“1”然后数字门的输出也必须处于逻辑电平“1”，因此，这种类型的逻辑门被称为 Inclusive-OR 功能。当A和B =“1”时，逻辑门的名称来自包括 Q =“1”的情况。

然而，逻辑输出当ONLYA =“1”或ONLYB =“1”但NOT同时在一起时获得“1”，给出二进制输入“01”或“10”，则输出为“1”。这种类型的门称为异或功能，或者更常见的是 Ex-Or 功能。这是因为当A和B都是“1”时，它的布尔表达式排除了“OR BOTH”Q =“1”的情况。

换言之，当其两个输入端子相对于彼此处于“不同”逻辑电平时，异或门ONLY的输出变为“高”。

输入端的奇数个逻辑“1”在输出端给出逻辑“1”。这两个输入可以处于逻辑电平“1”或逻辑电平“0”，给出布尔表达式： Q =（A⊕B）= A .B + A. B

异或门功能，或Ex-OR简而言之，通过将标准逻辑门组合在一起形成更复杂的门功能来实现，这些门功能广泛用于构建算术逻辑电路，计算逻辑比较器和错误检测电路。

双输入“异或” “gate基本上是模2加法器，因为它给出了两个二进制数的总和，因此在设计上比其他基本类型的逻辑门更复杂。真实表，逻辑符号和2输入异或“门的实现如下所示。

数字逻辑”异或“门

2输入异或门

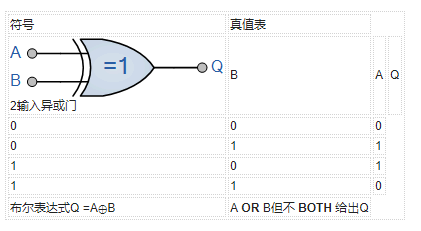
给出布尔表达式of：Q = A B + A B

上面的真值表显示异或门的输出仅为“高”时它的两个输入端都相对于每个输入端处于“不同”的逻辑电平河如果这两个输入A和B都处于逻辑电平“1”或两者都处于逻辑电平“0”，则输出为“0”，使得栅极为“奇数但不是偶数栅极”。换句话说，当输入中存在奇数个1时，输出为“1”。

异或门的这种能力比较两个逻辑电平和产生取决于输入条件的输出值在计算逻辑电路中非常有用，因为它给出了以下布尔表达式：

Q =（A⊕B）= A .B + A。 B

由2输入 Ex-OR实现的逻辑功能给出为：“ A OR B但不是”将在 Q 处给出输出。一般情况下，只有当门的输入端有ODD1时， Ex-OR 门才会给出逻辑“1”的输出值，如果两个数字相等，输出为“0”。

然后具有两个以上输入的 Ex-OR 函数称为“奇函数”或模2和（Mod-2-SUM），而不是 Ex-OR 。此描述可以扩展为适用于任意数量的单个输入，如下所示，用于3输入 Ex-OR 门。

3输入异或门

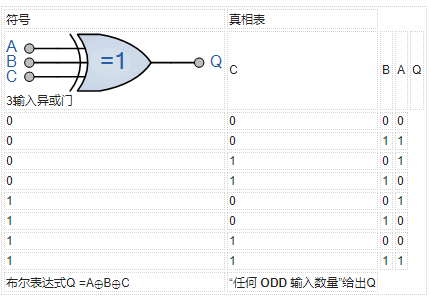
给予布尔表达式：Q = A BC + A B C + AB C + ABC

用于表示 Excl的符号usive-OR 奇数函数与标准的Inclusive-OR Gate略有不同。逻辑 OR 门的逻辑或布尔表达式是逻辑加法的逻辑加法，用标准加号表示。

用于描述<的布尔表达式的符号b>异或“函数是一个圆圈内的加号（ + ）（Ο）。此异或符号还表示数学“子对象的直接和”表达式，异或“函数的结果符号为：（⊕）。

我们之前说过， Ex-OR 功能不是基本的逻辑门，而是连接在一起的不同逻辑门的组合。使用上面的2输入真值表，我们可以将 Ex-OR 函数扩展为：（A + B）。（ AB ）这意味着我们可以使用以下单独的门实现这个新表达式。

异或门等效电路

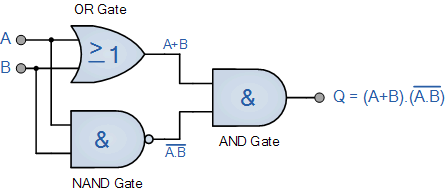
上面实现 Ex-OR 函数的一个主要缺点是它包含三种不同类型的逻辑门 OR ， NAND ，最后 AND 在其设计中。从单个门生成 Ex-OR 函数的一种更简单的方法是使用我们最喜欢的 NAND 门，如下所示。

Ex-或使用与非门实现功能

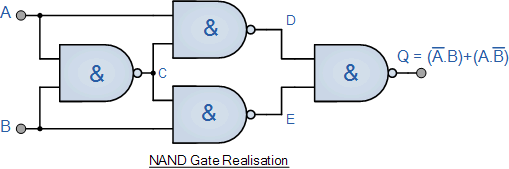
异或门主要用于构建执行算术运算和计算的电路，特别是加法器和半加法器，因为它们可以提供“进位”功能或作为受控逆变器，其中一个输入通过二进制数据和另一个输入提供控制信号。

通用数字逻辑异或门IC包括：

TTL逻辑Ex -OR Gates

74LS86 Quad 2-input

CMOS逻辑异或门

CD4030 Quad 2-input

7486四路2输入异或门

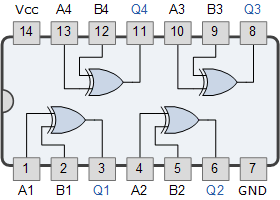
异或“逻辑功能是一种非常有用的电路，可用于许多不同类型的计算电路。虽然它本身不是一个基本的逻辑门，但它的实用性和多功能性已经把它变成了一个标准的逻辑函数，它有自己的布尔表达式，运算符和符号。 异或门可广泛用作标准四路双输入74LS86 TTL门或4030B CMOS封装。

其最常用的应用之一是作为基本逻辑比较器，当其两个输入位不相等时，产生逻辑“1”输出。因此，异或门具有称为奇函数的不等式状态。为了比较包含两个或更多位的数字，需要额外的异或门，74LS85逻辑比较器为4位宽。

在下一个关于数字逻辑门的教程中

b>，我们将看看数字逻辑 Exclusive-NOR 门，它通常被称为Ex-NOR门功能，用于TTL和CMOS逻辑电路以及它的布尔代数定义和真值表。