NOR门教程等效电路

异或非门功能是一个数字逻辑门，它是异或功能的反向或互补形式

基本上，“异或”门是一个组合异或门和非门，但有一个类似于标准NOR门的真值表，因为它的输出通常为逻辑电平“1”，当ANY时，输出“低”到逻辑电平“0”其输入处于逻辑电平“1”。

但是，仅当输入的BOTH处于相同逻辑电平时，才会获得输出“1” ，二进制“1”或“0”。例如，“00”或“11”。然后，此输入组合将给出布尔表达式：Q =（A⊕B）= AB + AB

然后输出数字当其两个输入端A和B处于“SAME”逻辑电平时，逻辑异或非门ONLY变为“高电平”，逻辑电平可以处于逻辑电平“ 1“或逻辑电平”0“。换句话说，其输入上的偶数个逻辑“1”在输出端给出逻辑“1”，否则在逻辑电平“0”。

然后这种类型的门给出并输出“ 1“当其输入”逻辑上等于“或”等效“时，这就是为什么有时会调用Exclusive-NOR门a等效门。

异或非门的逻辑符号只是一个带有圆或“反转气泡”的异或门，（ο）在其输出端代表NOT函数。然后逻辑异或非门是我们之前看到的异或门（A⊕B）的反向或“互补”形式。

Ex-NOR门等效

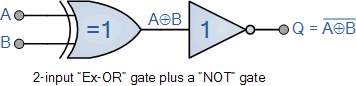
异或非门，也写成：“Ex-NOR”或“XNOR”，通过将标准门组合在一起形成更复杂的门功能来实现功能，下面给出了2输入 Exclusive-NOR 门的示例。

数字逻辑“Ex-NOR”门

2输入异或门

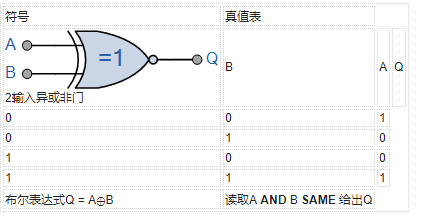
给出布尔表达式：Q = AB + AB

由2输入实现的逻辑功能NOR 门给出为“当A和B都是SAME ”时将给出 Q 的输出。通常，只有当栅极输入端有偶数1时，一个异或非门才会给出逻辑“1”的输出值（反向OR gate）除非所有输入均为“LOW”。

然后具有两个以上输入的 Ex-NOR 函数称为“偶函数”或modulo-2-sum（Mod-2-SUM），而不是 Ex-NOR 。该描述可以扩展为适用于任意数量的单个输入，如下所示，用于3输入 Exclusive-NOR 门。

3输入异或门

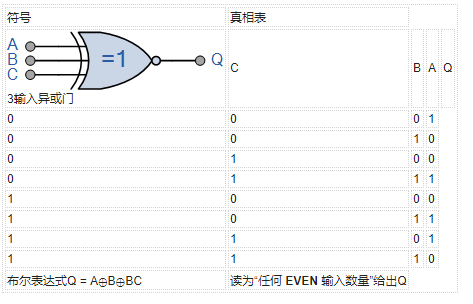
给出布尔表达式：Q = ABC + AB C + A B C + <跨度> A BC

我们之前说过， Ex-NOR 功能是不同基本逻辑门 Ex-OR 和 NOT 门的组合，并且通过使用在上面的2输入真值表中，我们可以将 Ex-NOR 函数扩展为： Q = A⊕B =（AB）+（ A 。 B ）这意味着我们可以使用以下单独的门来实现这个新表达式。

Ex-NOR门等效电路

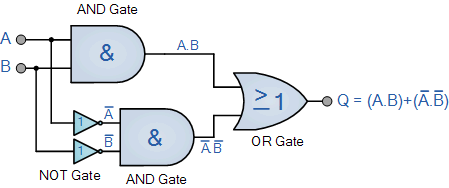
上面实现 Ex-NOR 函数的一个主要缺点是它包含三个不同的类型逻辑在其基本设计中对 AND ， NOT 以及最后一个 OR 门进行门控。从单门类型产生 NOR 功能的一种更简单的方法是使用 NAND 门，如下所示。

Ex-NOR功能实现使用与非门

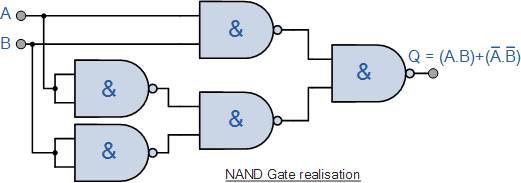
Ex-NOR 门主要用于电子电路执行算术运算和数据检查，例如 Adders ， Subtractors 或 Parity Checkers 等。作为 Ex-NOR 当两个输入相等时，门给出逻辑电平“1”的输出，它可用于比较两个二进制数字或数字的幅度，因此在数字比较器电路中使用 Ex-NOR 门。

常用的数字逻辑异或非门IC包括：

TTL Logic Ex-NOR Gates

74LS266 Quad 2-input

CMOS逻辑Ex-NOR门

CD4077 Quad 2-input

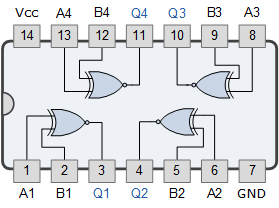
74266四路2输入异或非门

在下一个关于数字逻辑门的教程中，我们将看到数字三态缓冲器，也称为非反相缓冲器，用于TTL和CMOS逻辑电路以及其布尔代数定义和真相表。