

并联电阻的计算公式
描述
当两个端子分别连接到另一个电阻器或电阻器的每个端子时,称电阻器并联连接在一起
与前一个串联电阻器电路不同,在并联电阻器中网络电路电流可以采用多条路径,因为电流有多条路径。然后并联电路被归类为电流分压器。
由于电源电流有多条路径流过,并联网络中所有分支的电流可能不同。然而,并联电阻网络中所有电阻器的电压降是相同的。然后,并联的电阻在它们之间有一个公共电压,对于所有并联的元件都是如此。
因此我们可以定义并联电阻电路作为电阻器连接到相同的两个点(或节点)并且通过其具有连接到公共电压源的多于一个电流路径的事实来识别的电阻器。然后在下面的并联电阻示例中,电阻 R 1 两端的电压等于电阻 R 2 两端的电压等于 R 3 的电压等于电源电压。因此,对于并联电阻网络,其给出如下:
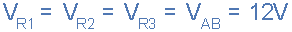
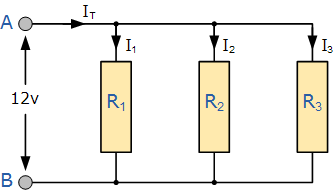
在以下电阻并联电路中的电阻 R 1 , R 2 和 R 3 两个点之间并联连接在一起 A 和 B ,如图所示。
并联电阻电路
在之前的串联电阻网络中,我们看到了总电阻 R T 电路等于加在一起的所有单个电阻的总和。对于并联电阻,等效电路电阻 R T 的计算方式不同。
这里,倒数( 1 / R )各个电阻的值全部加在一起而不是电阻本身与代数和的倒数给出等效电阻,如图所示。
并联电阻方程
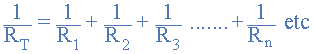
然后,并联连接的两个或多个电阻的等效电阻的倒数是各个电阻的倒数的代数和。
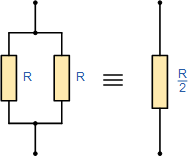
如果两个并联的电阻或阻抗相等且相同,则总电阻或等效电阻R T 为等于一个电阻值的一半。这等于R / 2和三个相等的并联电阻,R / 3等。
注意,等效电阻总是小于并联网络中的最小电阻,所以总电阻 R T 将随着附加的并联电阻的增加而减少。
并联电阻给出了一个称为电导的符号,符号G,其中电导单位为Siemens,符号S。电导是电阻的倒数或倒数,(G = 1 / R)。为了将电导转换回电阻值,我们需要取电导的倒数,然后将电阻器的总电阻 R T 并联。
我们现在知道连接在相同两点之间的电阻器是并联的。但是并联电阻电路可以采用除上面给出的明显形式之外的许多形式,这里是电阻器如何并联连接在一起的几个例子。
各种并联电阻网络
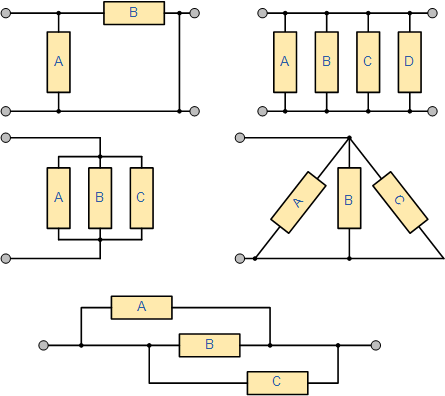
上面的五个电阻网络可能看起来彼此不同,但它们都被排列为并联的电阻因此,相同的条件和公式适用。
并联电阻器实例No1
求出总电阻, R T 以下电阻连接在并联网络中。
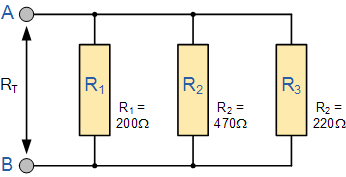
总电阻 R T 跨两个终端 A 和 B 计算如下:
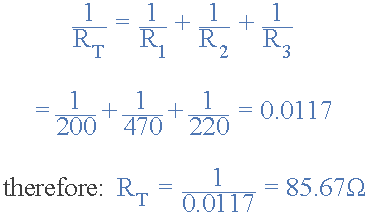
这种倒数计算方法可用于计算单个并行网络中连接在一起的任意数量的单个电阻。
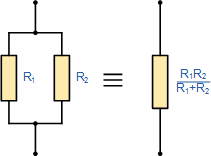
但是,如果只有两个并联的电阻,那么我们可以使用更简单,更快速的公式来找到总电阻或等效电阻值R T 并帮助减少倒数数学
这种更快的并行计算两个电阻的方法,具有相等或不相等的值,如下:

并联电阻器No2
考虑以下电路,并联组合中只有两个电阻器。
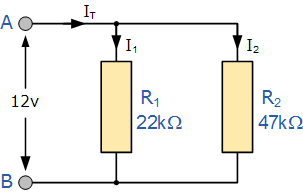
使用上面的公式将两个电阻并联连接在一起,我们可以计算总电路电阻, R T :
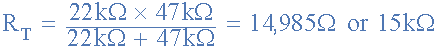
要记住并联电阻的一个要点是,t并联连接在一起的任何两个电阻的总电路电阻( R T )总是LESS,而不是最小电阻的值在上面的例子中,组合的值计算如下: R T =15kΩ,其中作为最小电阻的值22kΩ,更高。换句话说,并联网络的等效电阻将始终小于组合中最小的单个电阻。
此外,在 R 1 <的情况下/ span>等于 R 2 的值,即 R 1 = R 2 ,网络的总电阻恰好是其中一个电阻的值的一半, R / 2 。
同样,如果三个或更多电阻各有一个相同的值并联连接,则等效电阻将等于 R / n 其中 R 是电阻的值, n 是组合中单个电阻的数量。
例如,六个100Ω电阻以并联组合连接在一起。因此,等效电阻为: R T = R / n = 100/6 =16.7Ω。但请注意,这仅适用于等效电阻。那些电阻都具有相同的值。
并联电阻电路中的电流
总电流 I T 进入并联电阻电路是在所有并联支路中流动的所有单独电流的总和。但是流过每个并联支路的电流量可能不一定相同,因为每个支路的电阻值决定了该支路内流动的电流量。
例如,尽管并联组合具有电阻相同,电阻可能不同,因此流过每个电阻的电流肯定会因欧姆定律的不同而不同。
考虑上面并联的两个电阻。流过并联连接在一起的每个电阻( I R1 和 I R2 )的电流不是必须具有相同的值,因为它取决于电阻器的电阻值。但是,我们知道在 A 点进入电路的电流也必须在 B 点退出电路。
基尔霍夫电流定律指出:“离开电路的总电流等于进入电路的电流 - 没有电流丢失”。因此,在电路中流动的总电流如下:
I T = I R1 + I R2
然后使用欧姆定律,流经上述实例No2的每个电阻的电流可以计算为:
电流流动在 R 1 = V S ÷R 1 = 12V÷22kΩ=0.545mAor545μA
电流 R 2 = V S ÷R 2 = 12V÷47kΩ=0.255mAor255μA
因此给我们一个总电流 I T 在电路周围流动:
I T = 0.545mA + 0.255mA = 0.8mA或800μA
这也可以使用欧姆定律直接验证:
I T = V S ÷R T = 12÷15kΩ= 0.8mA或800μA (相同)
给出用于计算并联电阻电路中流动的总电流的公式,它是加在一起的所有单个电流的总和,给出如下:
I total = I 1 + I 2 + I 3 ... .. + I n
然后并联电阻网络也可以被认为是“电流分压器”,因为电源电流在各个并联支路之间分裂或分开。因此,具有 N 电阻网络的并联电阻器电路将具有N个不同的电流路径,同时保持其自身的公共电压。并联电阻也可以互换,而不会改变总电阻或总电路电流。
并联电阻No3
计算各个分支电流和从中抽取的总电流以下电阻组并联在一起的电源供电。
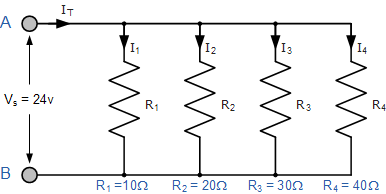
由于电源电压常见对于并联电路中的所有电阻,我们可以使用欧姆定律来计算单个支路电流,如下所示。
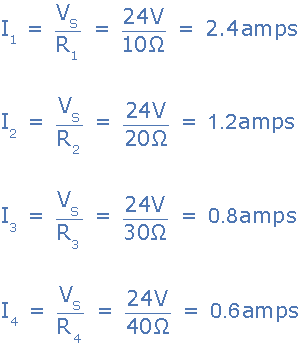
然后流入并联电阻器组合的总电路电流 I T 将为:
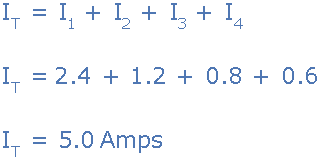
通过找到等效电路电阻 R T ,也可以找到并验证这个5安培的总电路电流值。并联支路并将其分为电源电压, V S 如下所示。
等效电路电阻:
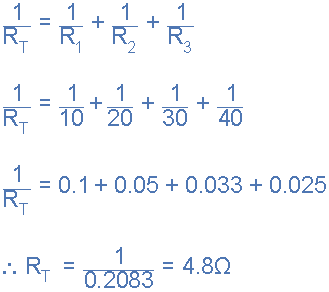
然后流入电路的电流将是:
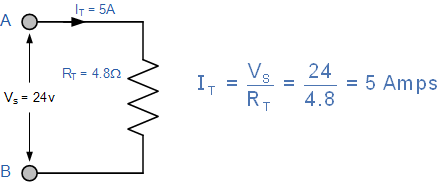
并联电阻器
总结一下。当连接两个或多个电阻器使得它们的两个端子分别连接到另一个或多个电阻器的每个端子时,它们被称为并联连接在一起。并联组合中每个电阻两端的电压完全相同,但流过它们的电流不相同,这取决于它们的电阻值和欧姆定律。然后并联电路是电流分压器。
并联组合的等效或总电阻 R T 通过相互加法和总电阻值求得将始终小于组合中最小的单个电阻器。并联电阻网络可以在同一组合内互换,而不会改变总电阻或总电路电流。即使一个电阻可能开路,并联电路中连接在一起的电阻也将继续工作。
到目前为止,我们已经看到电阻网络以串联或并联组合方式连接。在下一个关于电阻器的教程中,我们将同时以串联和并联组合方式将电阻连接在一起,从而产生混合或组合电阻电路。
-
功率的计算公式2009-02-24 26754
-
电阻衰减网络计算公式2008-04-21 7419
-
功率的计算公式/电功率计算公式2008-08-13 134592
-
常用体积计算公式2010-07-17 597524
-
并联电阻的等效计算公式2010-08-30 60603
-
电压为12伏的led串并联用限流电阻计算公式2011-07-01 18193
-
电感的计算公式2016-05-06 2534
-
电容降压原理和计算公式2016-06-22 2368
-
并联电阻计算公式 并联电阻阻值怎么计算2016-09-19 145728
-
LC谐振频率计算公式 LC串联和并联谐振频率计算2016-10-10 354301
-
串并联电路中的等效电阻计算公式2018-01-16 7006
-
电阻串联和并联的计算方法_电阻串联和并联的作用2018-01-21 219032
-
并联谐振电路的工作原理及计算公式2022-09-05 35079
-
电容与电阻并联计算公式2023-08-25 17736
-
电机扭矩的计算公式和转速计算公式2023-12-25 9360
全部0条评论

快来发表一下你的评论吧 !

