

串联电阻和并联电阻的计算方法
描述
电阻可以无限数量的串联和并联组合连接在一起形成复杂的电阻电路
在之前的教程中,我们学习了如何将各个电阻连接在一起形成一个系列电阻器网络或并联电阻器网络我们使用欧姆定律来查找流入的各种电流和每个电阻器组合的电压。
但是如果我们想要以“BOTH”并联和串联方式连接各种电阻器怎么办?在同一电路中组合产生更复杂的电阻网络,我们如何计算这些电阻组合的电路电阻,电流和电压的总和。
将串联和并联电阻网络组合在一起的电阻电路一般称为电阻器组合或混合电阻器电路。计算电路等效电阻的方法与任何单个串联或并联电路的方法相同,希望我们现在知道串联的电阻器承载完全相同的电流,并联的电阻器具有完全相同的电压。
例如,在以下电路中计算从12v电源获取的总电流( I T )。
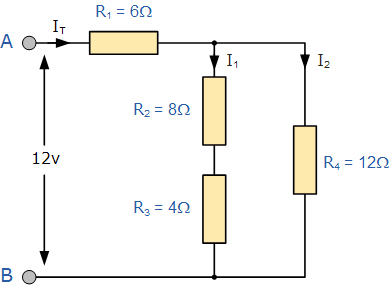
乍一看这似乎是一项艰巨的任务,但如果我们仔细观察,我们可以看到两个电阻, R 2 和 R 3 实际上都是以“SERIES”组合连接在一起所以我们可以将它们加在一起产生相同的电阻相同正如我们在串联电阻教程中所做的那样。因此,该组合的合成电阻为:
R 2 + R 3 =8Ω+4Ω=12Ω
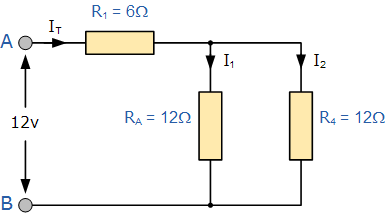
所以我们可以替换电阻 R 2 和 R 3 上面用一个电阻值12Ω
>>
所以我们的电路现在在“PARALLEL”中有一个电阻 R A ,电阻 R 4 。使用并联方程式中的电阻,我们可以使用以下两个并联电阻的公式将此并联组合减少到单个等效电阻值 R (组合) 。
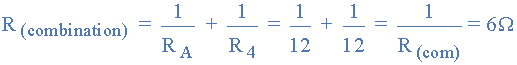
结果电阻电路现在看起来像这样:
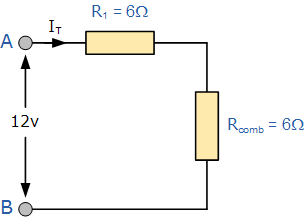
我们可以看到剩下的两个阻力, R 1 和 R (梳理) 以“SERIES”组合连接在一起,并且它们可以再次加在一起(电阻串联),以便点 A 和 B 因此给出:
R = R comb + R 1 =6Ω+6Ω= 12Ω
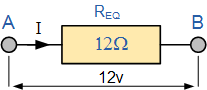
单电阻12Ω可用于替换原始电路中连接在一起的原始四个电阻。
现在使用欧姆定律,电路的值电流( I )简单计算如下:
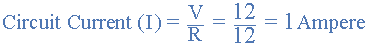
所以任何复杂的电阻电路通过使用上述步骤替换所有串联或并联连接在一起的电阻,可以将由几个电阻组成的电阻简化为只有一个等效电阻的简单单电路。
我们可以通过使用更进一步欧姆法找到两个分支电流, I 1 和 I 2 ,如图所示。
V (R1) = I * R 1 = 1 * 6 = 6伏
V (RA) = V R4 =(12 - V R1 )= 6伏
因此:
I 1 = 6V÷R A = 6÷12 = 0.5A或500mA
I 2 = 6V÷R 4 = 6÷12 = 0.5A或500mA
由于两个分支的电阻值在12Ω时相同,因此 I 1 和 I 2 每个也等于0.5A(或500mA)。因此,总电源电流 I T : 0.5 + 0.5 = 1.0安培,如上所述。
在进行这些更改后,使用复杂电阻组合和电阻网络绘制或重绘新电路有时会更容易,因为这有助于数学的视觉辅助。然后继续更换任何串联或并联组合,直到找到一个等效电阻 R EQ 。让我们尝试另一种更复杂的电阻组合电路。
串联电阻和并联电阻No2
求出等效电阻, R EQ 用于以下电阻器组合电路。
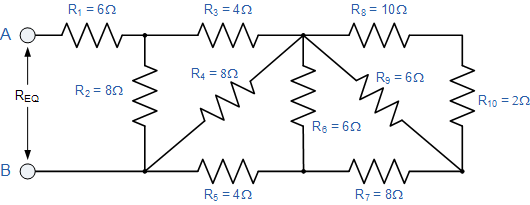
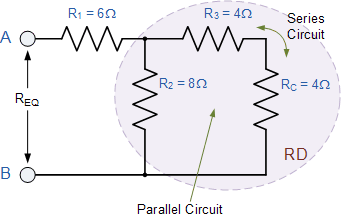
再次,乍一看这个梯形电阻网络似乎很复杂任务,但与以前一样,它只是连接在一起的串联和并联电阻的组合。从右侧开始并使用两个并联电阻的简化公式,我们可以找到 R 8 与 R 10 <的等效电阻/ sub> 组合并称之为 R A 。
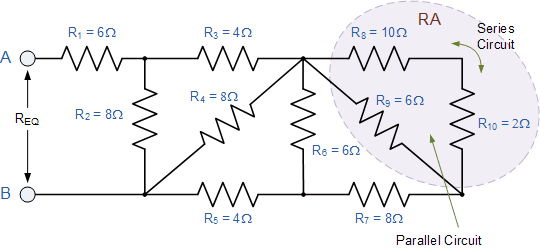
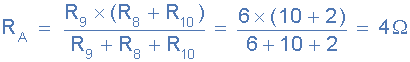
R A 与 R 7 因此总电阻 R A + R 7 = 4 + 8 =12Ω如图所示。
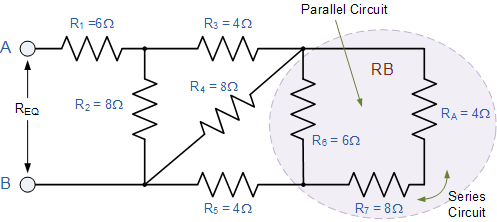
12Ω的电阻值现在为与 R 6 平行,可以计算为 R B 。
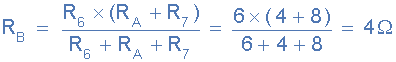
R B 与 R 5 因此总电阻 R B + R 5 = 4 + 4 =8Ω,如图所示。
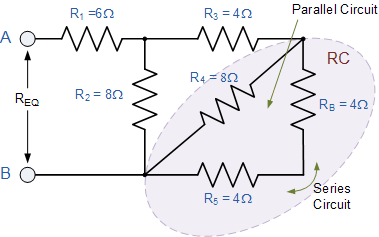
8Ω的电阻值现在与 R 4并联 并且可以计算为 R C ,如图所示。
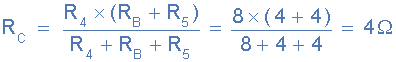
R C 与 R 3 串联,因此总电阻 R C + R 3 =8Ω如图所示。
8Ω的电阻值现在与 R 2 并联,我们可以从中计算 R D as:
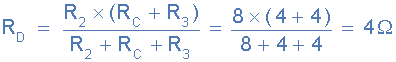
R D 与 R 1 串联,因此总电阻 R D + R 1 = 4 + 6 =10Ω如图所示。
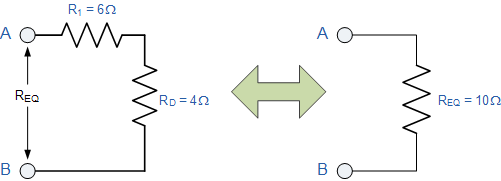
然后复杂的组合上面的电阻网络包括十个串联连接在一起的独立电阻,并联组合可以用一个等效电阻( R EQ )代替10Ω。
解决任何组合抗蚀剂时或者由串联和并联支路的电阻组成的电路,我们需要采取的第一步是识别简单的串联和并联电阻支路,并用等效电阻代替它们。
这一步将使我们能够降低电路的复杂性,帮助我们将复杂的组合电阻电路转换成单个等效电阻,记住串联电路是分压器,并联电路是电流分压器。
然而,计算更复杂的T-焊盘衰减器和电阻桥网络不能简化为使用等效电阻的简单并联或串联电路,需要采用不同的方法。这些更复杂的电路需要使用Kirchhoff的电流定律和Kirchhoff的电压定律来解决,这将在另一个教程中讨论。
在下一个关于电阻器的教程中,我们将会看到在两个点(包括电阻器)的电位差(电压)处。
-
并联电阻的基本原理、计算方法及影响因素2024-07-29 17126
-
电阻串联和并联哪个电阻大2023-09-14 14337
-
串联和并联组合电阻器2023-09-01 5261
-
led电阻器如何工作的,led电阻计算方法2023-07-20 5306
-
变频器制动电阻设计计算方法2023-01-03 12289
-
电阻的串联和并联阻值怎么计算?2021-05-01 52719
-
升压电路取样电阻的计算方法2021-04-06 1769
-
并联谐振串联谐振计算方法介绍2020-06-19 5414
-
绕线电阻的计算方法_绕线电阻的制作过程2018-01-24 22938
-
电阻串联与并联有什么区别_电阻串联和并联的区别2018-01-21 149077
-
用DrDAQ证明串联和并联电阻的公式2017-06-21 2729
-
贴片电阻串联和并联的作用2017-03-16 5869
-
如何识别色环电阻 色环电阻计算方法读数2016-09-23 132405
-
并联电阻计算公式 并联电阻阻值怎么计算2016-09-19 145754
全部0条评论

快来发表一下你的评论吧 !

