

RC区分器电路公式输出及波形案例摘要
描述
无源RC微分器是一个串联RC网络,它产生的输出信号对应于微分的数学过程。
对于无源RC微分电路,输入连接到电容输出电压来自与 RC积分电路完全相反的电阻。
无源RC微分器只不过是与电阻串联的电容这是一种频率相关器件,它具有与固定电阻串联的电抗(与积分器相反)。就像积分电路一样,输出电压取决于电路RC时间常数和输入频率。
因此在低输入频率时,电容的电抗,X C 是高阻断任何直流电电压或缓慢变化的输入信号。在高输入频率时,电容电抗很低,允许快速变化的脉冲直接从输入端传递到输出端。
这是因为容抗电容的比率(X C )对于不同的频率,电阻(R)是不同的,频率越低,输出越少。因此,对于给定的时间常数,随着输入脉冲的频率增加,输出脉冲越来越像输入脉冲的形状。
我们在关于被动高通的教程中看到了这种效应滤波器,如果输入信号是正弦波,rc微分器将简单地用作具有与RC对应的截止或转角频率的简单高通滤波器(HPF)串联网络的时间常数(tau,τ)。
因此,当用纯正弦波馈电时,由于标准,RC微分电路作为简单的无源高通滤波器。 X C = 1 /(2πC)的容抗电阻公式。
但也可以配置一个简单的RC网络来执行输入信号的微分。我们从之前的教程中知道,通过电容器的电流是一个复数指数,由下式给出: i C = C(dVc / dt)。电容器充电(或放电)的速率与电阻量和电容量成正比,给出电路的时间常数。因此,RC微分电路的时间常数是等于R和C乘积的时间间隔。考虑下面的基本RC串联电路。
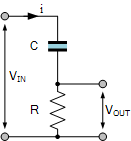
RC微分电路
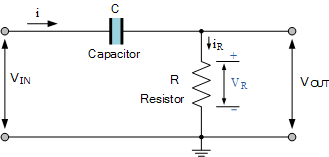
对于RC微分电路,输入信号施加到电容的一侧,输出通过电阻,然后V OUT 等于V R 。由于电容器是频率相关元件,所以在板上建立的电荷量等于电流的时域积分。也就是说,电容器需要一定的时间才能完全充电,因为电容器不能立即以指数方式充电。
我们在教程中看到 RC积分器单级电压脉冲施加到RC积分器的输入端,如果RC时间常数足够长,则输出变为锯齿波形。 RC微分器也将改变输入波形,但与积分器的方式不同。
电阻器电压
我们之前说过,对于RC微分器,输出等于电阻两端的电压,即:V OUT 等于V R 并且是一个电阻,输出电压可以然而,电容器两端的电压不能立即改变,而是取决于电容C的值,因为它试图在其板上存储电荷Q.然后,流入电容器的电流,即 i t 取决于电路板上电荷的变化率。因此,电容器电流与电压不成比例,而与其时间变化成正比,给出:i = dQ / dt。
当电容器极板上的电荷量等于 Q = C x Vc ,即电容乘以电压时,我们可以推导出电容器电流的公式为:
电容器电流
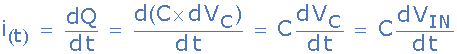
因此电容器电流可写为:

由于V OUT 等于V R ,其中V R 根据欧姆定律也是相等的:i R xR。流过电容器的电流也必须流过电阻,因为它们都串联连接在一起。因此:
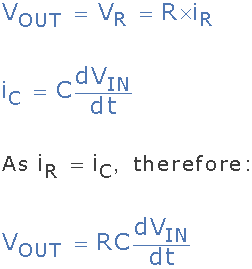
因此,为RC微分电路提供的标准公式为:
RC微分公式

然后我们可以看到输出电压V OUT 是输入电压的导数,V IN ,由RC的常数加权。其中RC表示串联电路的时间常数τ。
单脉冲RC微分器
当首次将单步电压脉冲施加到输入时对于RC微分器,电容器“最初出现”为快速变化信号的短路。这是因为方波的正向边缘的斜率dv / dt非常大(理想情况下是无限的),因此在信号出现的瞬间,所有输入电压都会通过电阻器出现的输出。
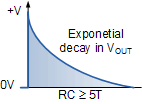
在输入信号的初始正向边沿经过并且输入的峰值恒定后,电容开始充电它的正常方式是通过电阻响应输入脉冲,其速率由RC时间常数τ= RC决定。
当电容充电时,电阻两端的电压,输出降低以指数方式,直到电容器在5RC(5T)的时间常数后变为完全充电,导致电阻器上的输出为零。因此,满充电电容两端的电压等于输入脉冲的值,如下:V C = V IN ,只要输入脉冲的幅度,这个条件就成立不会改变。
如果输入脉冲现在变化并返回到零,则脉冲的负向边沿的变化率通过电容器到达输出,因为电容器无法响应高dv / dt变化。结果是输出端出现负向峰值。
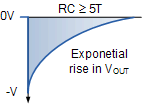
在输入信号的初始负向边沿后,电容器恢复并启动正常放电,电阻上的输出电压,以及输出电压随着电容放电而开始呈指数增长。
因此,无论何时输入信号快速变化,输出端都会产生电压尖峰。该电压尖峰的极性取决于输入是在正方向还是在负方向上变化,因为输入信号的正向边沿产生正尖峰,并且由于负输出而产生负尖峰。输入信号。
因此,RC微分器输出实际上是输入信号的变化率图,它与方波输入波没有相似之处,但由于输入脉冲值改变时由窄正负尖峰组成。
通过改变方波输入脉冲的时间周期T相对于串联组合的固定RC时间常数,输出脉冲的形状将如图所示改变。
RC微分器输出波形
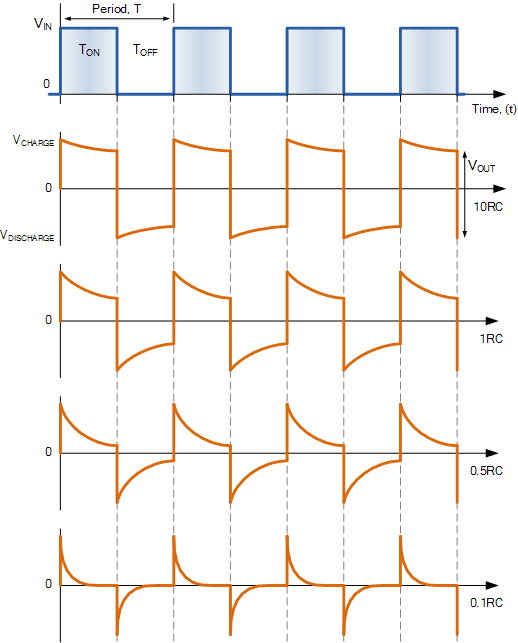
然后我们可以看到输出波形的形状取决于脉冲宽度的比例到RC时间常数。当RC比脉冲宽度大得多(大于10RC)时,输出波形类似于输入信号的方波。当RC比脉冲宽度小得多(小于0.1RC)时,输出波形采用非常尖锐和窄的尖峰形式,如上所示。
因此通过改变10RC电路的时间常数到0.1RC我们可以产生一系列不同的波形。通常在RC微分电路中总是使用较小的时间常数,以在R上的输出端提供良好的尖锐脉冲。因此,方波脉冲的差分(高dv / dt阶跃输入)是无限短的尖峰,导致RC微分电路。假设方波波形的周期T为20mS,脉冲宽度为10mS(20mS除以2)。为使尖峰放电至其初始值的37%,脉冲宽度必须等于RC时间常数,即RC = 10mS。如果我们选择一个电容值,C为1uF,则R等于10kΩ。
为使输出类似于输入,我们需要RC为脉冲宽度值的十倍(10RC),因此,对于电容值,例如1uF,这将给出一个电阻值:100kΩ。同样,为了使输出类似于尖锐脉冲,我们需要RC为脉冲宽度的十分之一(0.1RC),因此对于相同的电容值1uF,这将给出一个电阻值:1kΩ,依此类推。
RC分化器示例
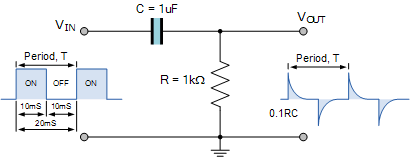
因此RC值为脉冲的十分之一宽度(在我们的例子中,这是0.1 x 10mS = 1mS)或更低,我们可以在输出端产生所需的尖峰,并且给定脉冲宽度的RC时间常数越低,尖峰越尖锐。因此,输出波形的确切形状取决于RC时间常数的值。
RC微分器摘要
我们在这里看到RC微分器教程,输入信号施加到电容器的一侧,输出通过电阻器。微分电路用于产生定时电路应用的触发或尖峰型脉冲。
当该RC电路应用方波步进输入时,它会在输出端产生完全不同的波形。输出波形的形状取决于输入方波的周期时间T(因此频率,f)和电路的RC时间常数值。
当输入波形的周期时间电路RC时间常数也类似于(或更高频率),输出波形类似于输入波形,即方波轮廓。当输入波形的周期时间远长于(较低频率)电路RC时间常数时,输出波形类似于窄的正和负尖峰。
输出的正尖峰由输入方波的前沿,而输出的负尖峰是由输入方波的下降沿产生的。然后RC微分电路的输出取决于输入电压的变化率,因为效果非常类似于微分的数学函数。
-
方波经过rc电路后的波形变化大吗2024-07-23 3355
-
方波通过RC成为了什么波形2024-07-22 5873
-
labview公式波形里的公式2024-01-07 3049
-
什么是rc电路的时间常数呢?2023-11-21 6450
-
如果输入占空比为50%的方波到一个RC电路,输出是什么波形?2023-10-24 3579
-
桥式整流器输出电压波形特性和计算公式2023-06-20 25059
-
你需要了解的RC电路波形2023-05-19 5859
-
一文读懂无源RC微分器电路2023-03-13 2139
-
不同RC波形频率响应2019-06-27 12402
-
什么是rc一阶电路的零输出响应2017-11-01 19405
-
带负反馈电路的RC电桥振荡器2009-11-28 1331
-
RC正弦波发生器及波形变换2009-03-17 10236
-
rc振荡电路频率计算公式2008-10-30 95505
-
RC滤波电路的计算及公式2008-10-21 53768
全部0条评论

快来发表一下你的评论吧 !

