频率响应曲线增益案例摘要

放大器或滤波器的频率响应显示输出增益如何响应不同频率的输入信号

放大器和滤波器是广泛使用的具有放大和滤波特性的电子电路因此，它们的名称。

放大器产生增益，而滤波器改变电信号相对于其频率的幅度和/或相位特性。由于这些放大器和滤波器在其设计中使用电阻器，电感器或电容器网络（RLC），因此这些电抗元件的使用与电路频率响应特性之间存在重要关系。

处理AC时电路假设它们以固定频率工作，例如50Hz或60Hz。但是，线性交流电路的响应也可以用恒定幅度但具有变化频率的交流或正弦输入信号来检查，例如在放大器和滤波器电路中发现的那些。然后，这允许使用频率响应分析来研究这样的电路。

电气或电子电路的频率响应使我们能够准确地看到输出增益（称为幅度响应）和相位（称为相位响应）在特定的单一频率或从0Hz，（dc）到数千的不同频率的整个范围内变化兆赫兹，（MHz）取决于电路的设计特性。

一般来说，电路或系统的频率响应分析是通过绘制其增益，即输出信号的大小来表示的。其输入信号，输出/输入与电路或系统预期工作的频率范围相对应。然后，通过了解每个频率点的电路增益（或损耗），有助于我们了解电路在不同频率信号之间的区别（或不良）。

给定频率的频率响应电路可以显示为幅度（增益）与频率（ƒ）的图形草图。水平频率轴通常以对数标度绘制，而表示电压输出或增益的垂直轴通常以十进制分度绘制为线性标度。由于系统增益可以是正的也可以是负的，因此y轴可以同时具有正值和负值。

在电子设备中，对数或简称“log”定义为必须提高基数以获得该数字的功率。然后在波德图上，对数x轴刻度以 log 10 分度渐变，因此每十倍频率（例如，0.01,0.1,1,10,100） ，1000等，在x轴上等间隔。与对数相反的是反对数或“反对数”。

频率响应曲线的图形表示称为波特图，因此波德图通常被认为是半 - 对数图，因为一个标度（x轴）是对数而另一个（y轴）是线性的（log-lin图），如图所示。

频率响应曲线

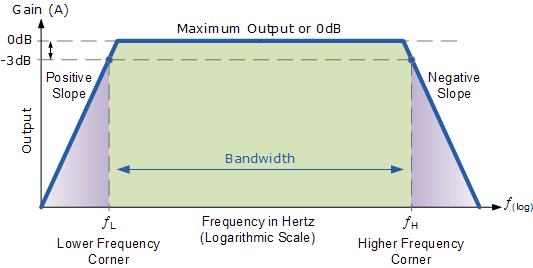
然后我们可以看到任何给定电路的频率响应是其行为的变化与输入信号频率的变化，因为它显示了频段输出（和增益）保持相当恒定的频率。 ƒ L 和ƒ H 之间的大小频率范围称为电路带宽。因此，我们能够一目了然地确定给定频率范围内任何正弦输入的电压增益（以dB为单位）。

如上所述，伯德图是频率响应的对数表示。大多数现代音频放大器具有平坦的频率响应，如上所示，在20 Hz至20 kHz的整个音频范围内。音频放大器的这个频率范围称为带宽（BW），主要由电路的频率响应决定。

频率点ƒ L 和ƒ H 与下角或截止频率有关，上角或截止频率点分别为电路增益从高处下降和低频率。频率响应曲线上的这些点通常称为-3dB（分贝）点。所以带宽简单地给出如下：

分贝，（dB）是1/10 是用于测量增益的常见非线性单位，定义为 20log 10 （A）其中 是十进制增益，绘制在y轴上。零分贝（0dB）对应于单位的幅度函数，给出最大输出。换句话说，当 Vout = Vin 时会出现0dB，因为在此频率级别没有衰减，并且给出如下：

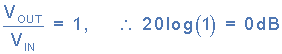
我们从上面的Bode图中看到，在两个角落或截止频率点，输出从0dB下降到-3dB并继续以固定速率下降。这种下降或增益的减小通常被称为频率响应曲线的滚降区域。在所有基本的单阶放大器和滤波器电路中，该滚降率定义为20dB / decade，相当于6dB /倍频程的速率。这些值乘以电路的顺序。

这些-3dB转角频率点定义了输出增益降至其最大值的70.71％的频率。然后我们可以正确地说-3dB点也是系统增益降低到其最大值的0.707的频率。

频率响应-3dB点

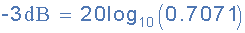
-3dB点也称为半功率点，因为此拐角频率的输出功率将是其最大0dB值的一半，如图所示。

因此，在截止频率下，输出到负载的输出功率有效“减半”，因此带宽（BW）频率响应曲线也可以定义为这两个半功率点之间的频率范围。

对于电压增益，我们使用 20log 10 （Av），对于当前增益 20log 10 （Ai），对于功率增益，我们使用 10log 10 （ AP） 。注意，乘法因子20并不意味着它是10的两倍，因为分贝是功率比的单位而不是实际功率水平的度量。 dB的增益也可以是正的或负的，正值表示增益，负值衰减。

然后我们可以在下表中呈现电压，电流和功率增益之间的关系。

分贝增益等价

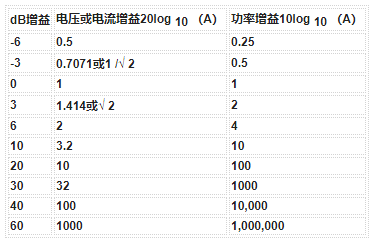
分贝示例e No1运算放大器可以具有开环电压增益，（ A VO ）超过1,000,000或100dB。

如果电子系统在施加12mV信号时产生24mV输出电压，则计算系统输出电压的分贝值。

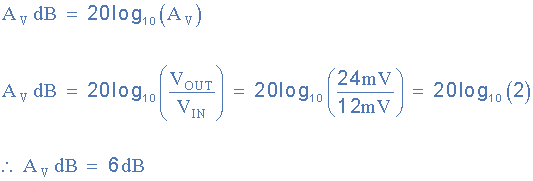
分贝示例No2

如果音频放大器的输出功率在信号频率为1kHz时测量为10W，而在信号频率为10kHz时测量为1W。计算功率的dB变化。

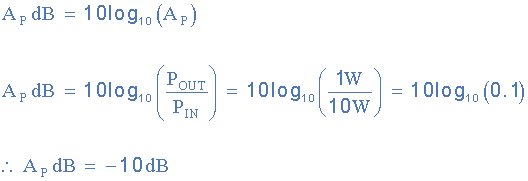
频率响应摘要

在本教程中，我们已经看到了频率范围电子电路工作的是由其频率响应决定的。器件或电路的频率响应通过显示其增益或其允许的信号量随频率变化来描述其在指定信号频率范围内的操作。

波特图是图形表示电路频率响应特性因此可用于解决设计问题。通常，电路增益幅度和相位函数使用沿x轴的对数频率刻度显示在单独的图形上。

带宽是电路在其上下切割之间工作的频率范围 - 关闭频率点。这些截止或拐角频率点表示与输出相关的功率下降到其最大值的一半的频率。这些半功率点对应于相对于其最大dB值的3dB增益（0.7071）的下降。

大多数放大器和滤波器具有平坦的频率响应特性，其中电路的带宽或通带部分是在很宽的频率范围内保持平坦且恒定。谐振电路设计用于通过一系列频率并阻止其他频率。它们使用电阻，电感和电容构建，其电抗随频率变化，它们的频率响应曲线看起来像一个急剧的上升或点，因为它们的带宽受共振的影响，这取决于谐振的 Q 。电路，作为更高的 Q 提供更窄的带宽。