

复数和相量运算复数定义及案例转换汇总
描述
电气工程中使用的数学将电阻,电流或直流电压加在一起使用所谓的“实数”,用作整数或分数。
但实数不是我们需要使用的那种数字,特别是在处理频率相关的正弦源和矢量时。除了使用正常数字或实数之外,还引入了复数,以便使用负数的平方根,√ 来解决复杂方程式。 1 。
在电气工程中,这种类型的数字称为“虚数”,为了区分虚数和实数,字母“ j ”已知通常在电气工程中使用j-operator。因此,字母“ j ”放在实数前面以表示其虚数操作。
虚数的例子是: j3 , j12 , j100 等。然后复数由两个不同但非常相关的部分组成,“实数”加上“虚数” “。
复数表示二维复数或s平面中以两个不同轴为参照的点。水平轴称为“实轴”,而垂直轴称为“虚轴”。复数的实部和虚部分别缩写为Re(z)和Im(z)。
由实数(有效成分)和虚数(无功成分)组成的复数)数字可以加上,减去和使用,与用基本代数分析直流电路完全相同。
数学中用于加减虚数的规则和定律与对于实数,j2 + j4 = j6等。唯一的区别在于乘法,因为两个虚数相乘在一起变为负实数。实数也可以被认为是一个复数,但假想零部分标记为j0。
j-operator的值恰好等于√ -1 ,因此“ j ”,( jxj )的连续乘法将导致 j 具有以下值为 -1 , -j 和 +1 。由于j运算符通常用于指示向量的逆时针旋转,因此每个连续的乘法或幂“ j ”, j 2 ,j 3 等将迫使矢量沿逆时针方向旋转固定角度90° o ,如下所示。同样,如果向量的乘法产生 -j 运算符,则相移将为-90 o ,即顺时针旋转。
矢量旋转的j运算符
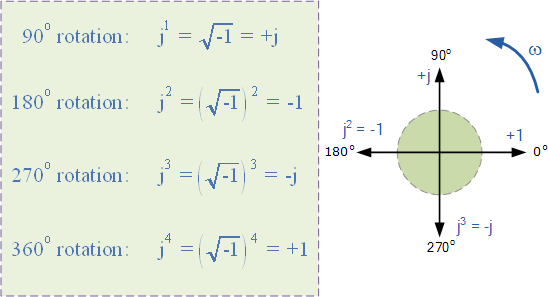
因此,通过将虚数乘以 j 2 将向量旋转 180 o 逆时针旋转,乘以 j 3 旋转 270 o 并通过 j 4 将其旋转 360 o 或回到原来的位置。乘以 j 10 或 j 30 将导致向量逆时针旋转适当的量。在每次连续旋转中,矢量的大小始终保持不变。
在电气工程中,有不同的方式以图形或数学方式表示复数。使用余弦和正弦规则的一种方法称为笛卡尔或矩形形式。
使用矩形形式的复数
在关于Phasors的最后一个教程中,我们看到一个复数由一个实部和一个虚部表示,它采用通用形式:

其中:
Z - 是代表向量的复数
x - 是实部或活动部件
y - 是虚部或反应部件
j - 由√ -1
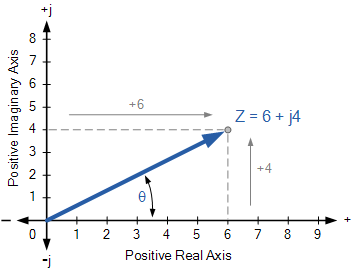
定义在矩形形式中,复数可以表示为二维点平面称为复合或s-plane。因此,例如, Z = 6 + j4 表示单个点,其坐标在水平实轴上表示6,在垂直虚轴上表示4,如图所示。
使用复数复杂或s面
但是,由于矩形形式的复数的实部和虚部都可以是正数或负数,因此实轴和虚轴都必须同时扩展。正面和负面的方向。然后产生一个复杂的平面,有四个象限,称为Argand Diagram,如下所示。
四象限Argand图
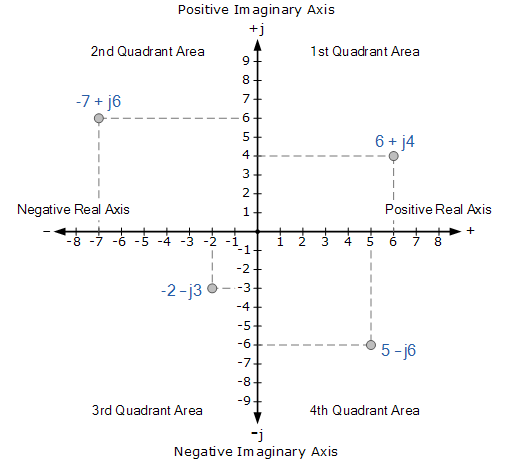
在Argand图上,横轴表示垂直虚轴右侧的所有正实数,以及垂直虚轴左侧的所有负实数。所有正虚数都表示在水平轴上方,而所有负虚数都低于水平实轴。然后生成一个二维复平面,其中有四个不同的象限,标记为 QI , QII , QIII 和 QIV 。
上面的Argand图也可用于表示旋转相量作为复平面中的一个点,其半径由相量的大小给出,每个将围绕它绘制一个完整的圆2π/ω秒。
然后我们可以进一步扩展这个想法,以显示旋转90° o 的极坐标和矩形形式的复数的定义。
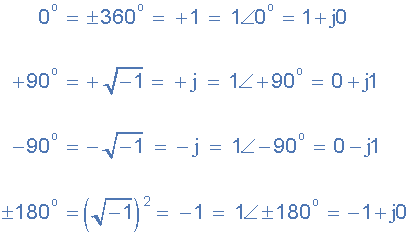
复数也可以有“零”实部或虚部等as: Z = 6 + j0 或 Z = 0 + j4 。在这种情况下,点直接绘制在实轴或虚轴上。此外,复数的角度可以使用简单的三角法计算,以计算直角三角形的角度,或者从正实轴开始沿着Argand图逆时针测量。
然后角度0和90 o 将位于第一象限( I ),角度(θ)介于90和180之间 o 在第二象限( II )。第三象限( III )包括180到270 o 之间的角度,而完成整个圆圈的第四个和最后一个象限( IV )包括270和360之间的角度 o 等。在所有四个象限中,相关角度可以从以下位置找到:
tan -1 (虚构成分÷实部成分)
复数的加法和减法
复数的加或减可以数学方式或以矩形形式进行图形化。另外,实际部分首先加在一起形成和的实部,然后虚部形成和的虚部,这个过程如下使用两个复数 A 和 B 作为示例。
复杂的加法和减法
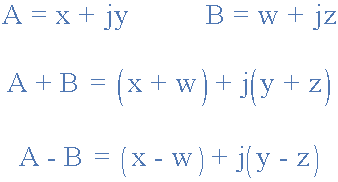
复数示例No1
两个向量分别定义为 A = 4 + j1 和 B = 2 + j3 。确定矩形( a + jb )形式的两个向量的和与差,并以图形方式确定为Argand图。
数学加法和减法
<跨度>加成
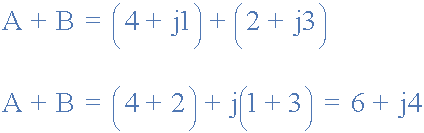
减法
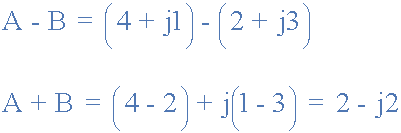
图形添加和减法
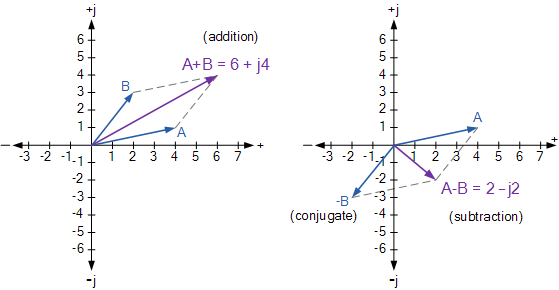
复数的乘法和除法
矩形形式中复数的乘法或多或少跟随与正规代数相同的规则以及运算符的连续乘法的一些附加规则,其中: j 2 = - 1 。因此,例如,将 A = 4 + j1 和 B = 2 + j3 的两个向量相乘,将得到以下结果。
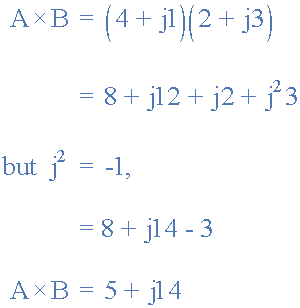
数学上,矩形复数的划分有点难以执行,因为它需要使用分母共轭函数将等式的分母转换为实数。这被称为“合理化”。然后,复数的划分最好使用“Polar Form”进行,我们将在后面介绍。但是,作为矩形形式的示例,我们可以找到vector A 的值除以vector B 。
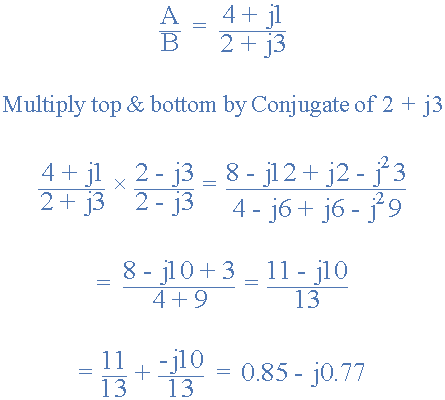
复共轭
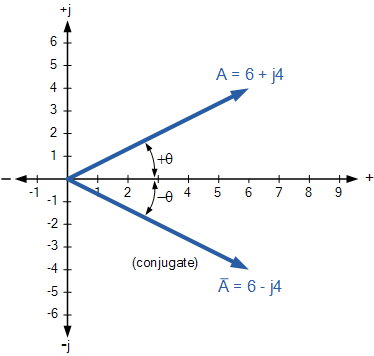
复共轭,或简单地共轭复数是通过反转代数符号找到的复数虚数仅在保持实数的代数符号相同的同时识别 z的复共轭使用符号 z 。例如, z = 6 + j4 的共轭是 z = 6-j4 ,同样 z = 6-的共轭j4 是 z = 6 + j4 。
复共轭的Argand图上的点在水平位置上具有相同的水平位置。实轴作为原始复数,但垂直位置相反。因此,复共轭可以被认为是复数的反映。以下示例显示复数, 6 + j4 及其在复平面中的共轭。
共轭复数
如上所述,复数与其复共轭的总和将始终为实数。然后,添加复数及其共轭仅将结果作为实数或有效分量,而它们的减法仅给出虚数或无功分量。复数的共轭是电气工程中用于确定使用矩形形式的交流电路的视在功率的重要元素。
使用极坐标形式的复数
与矩形形式不同在复平面中绘制点,复数的极坐标是根据其大小和角度编写的。因此,极坐标形式向量表示为: Z =A∠±θ,其中: Z 是极坐标形式的复数, A 是矢量的大小或模数,θ是 A 的角度或参数,可以是正数也可以是负数。该点的大小和角度仍然与上面的矩形形式相同,这次以极坐标形式表示点的位置以“三角形”表示,如下所示。
极性形式表示复数
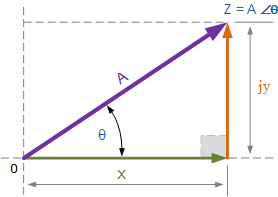
由于点的极坐标表示基于三角形,我们可以使用三角形的简单几何,尤其是三角形和毕达哥拉斯在三角形上的定理,以找出复数的大小和角度。正如我们从学校记得的那样,三角学处理边的关系和三角形的角度,因此我们可以将边之间的关系描述为:
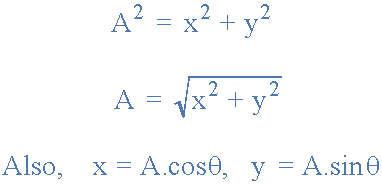
再次使用三角法,给出 A 的角度θ如下。

然后以Polar形式显示 A 的长度及其角度表示复数而不是点。同样以极性形式,复数的共轭具有相同的大小或模量,它是角度变化的符号,因此例如6∠30 o 将6∠-30 o 。
在矩形形式和极坐标形式之间转换
在矩形形式中,我们可以根据其直角坐标表示矢量,水平轴是其实轴,垂直轴是其虚轴或j分量。在极坐标形式中,这些实轴和虚轴简单地用“A∠θ”表示。然后使用上面的例子,矩形和极形之间的关系可以定义为。
将极性形式转换为矩形,(P→R)
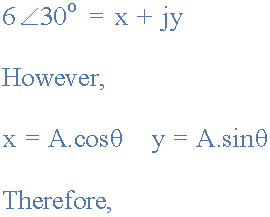
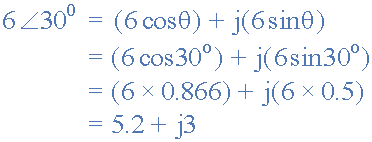
我们还可以将矩形转换回极性形式,如下所示。
将矩形转换为极坐标形式,(R→P)
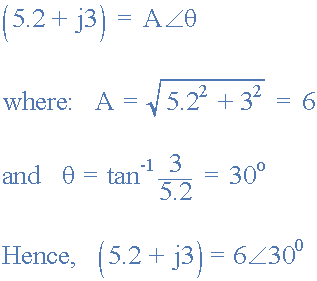
极地形式乘法和除法
矩形如上所述,形式最适合添加和减去复数,但极性形式通常更适合乘法和除法。为了将极坐标形式的两个向量相乘,我们必须首先将两个模数或大小相乘,然后将它们的角度加在一起。
极坐标中的乘法
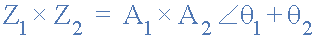
将6∠30 o 和8∠-45 o相乘 给我们。
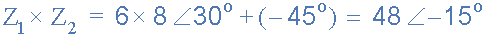
极地分裂
同样,分开两个极性形式的矢量,我们必须将两个模数分开然后减去它们的角度,如图所示。
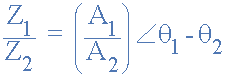
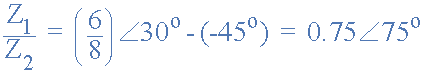
幸运的是,今天的现代科学计算器内置了数学函数(检查你的书),允许轻松转换矩形到极性形式( R→P ),然后从极性变为矩形,( R→P )。
使用指数形式的复数
到目前为止,我们已经考虑了矩形形式中的复数,( a + jb )和极地形式,(A∠±θ)。但是还有第三种表示复数的方法,该方法类似于对应于正弦曲线的长度(幅度)和相位角的极坐标形式,但使用自然对数的基数, e =2.718 281 .. 找到复数的值。第三种方法称为指数形式。
指数形式使用正弦的三角函数( sin )和直角三角形的余弦( cos )值,将复指数定义为复平面中的旋转点。寻找点位置的指数形式基于Euler's Identity,以瑞士数学家Leonhard Euler命名,并给出:
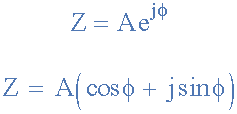
然后欧拉的身份可以用复平面上的以下旋转相量图表示。
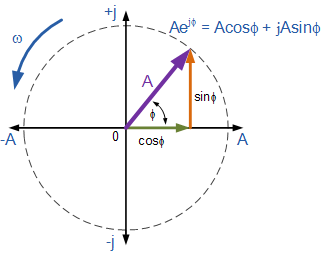
我们可以看到Euler的身份与上面的极性形式非常相似,并且它向我们显示了一个数字,例如 A e jθ 幅度为1的>也是一个复数。我们不仅可以将指数形式的复数转换为极性形式,例如: 2 e j30 =2∠30, 10 j120 =10∠120或 -6 j90 = - 6∠90,但欧拉的身份也为我们提供了一种将复数从指数形式转换为矩形形式的方法。然后,在定义复数时,指数,极坐标和矩形之间的关系给出为。
复数形式
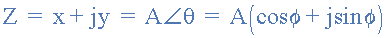
相量符号
到目前为止,我们已经看到了表示旋转的不同方式矢量或固定矢量使用复数来定义复杂平面上的点。相量符号是构造具有给定正弦波形的幅度和相位角的单个复数的过程。
然后相量符号或相量变换,因为它有时被称为,传递真实部分正弦函数: A (t) = A m cos(ωt±Φ)从时域到复数域,也被称为频域。例如:
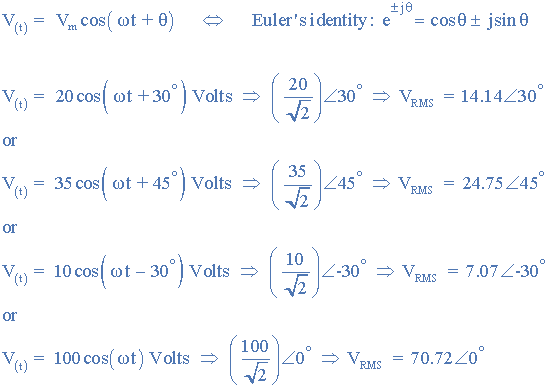
请注意√ 2 将最大振幅转换为a <有效或RMS值,相位角以弧度表示,(ω)。
复数汇总
然后总结本教程关于复杂数字以及在电气工程中使用复数。
复数由两个不同的数字组成,一个实数加上一个虚数。
虚数通过使用j与实数区分开来-operator。
前面带有字母“ j ”的数字将其标识为复合体中的虚数平面。
根据定义,j-operator j≡√ -1
可以添加,减去,乘以虚数
“ j ”乘以“ j “给出 j 2 = - 1
在矩形表格中,复数表示为复杂平面上的空间点。
在Polar Form中,复数由一条线表示,其长度为幅度和相位角。 / li>
在指数形式中,复数由一条线和相应的角度表示,该角度使用自然对数的底数。
复数可以用以下三种方式之一表示:
Z = x + jy »矩形表格
Z =A∠Φ»极地形式
Z = A jΦ »指数形式
Euler的身份可用于转换复杂从指数形式到矩形的数字。
在前面的教程中,我们已经看到我们可以使用相量来表示正弦波形,并且它们的幅度和相位角可以写在形式复杂的数字。我们还看到复数可以以矩形,极坐标或指数形式呈现,每个复数代数形式之间的转换包括加法,减法,乘法和除法。
在接下来的几个与AC串联电路中的相量关系相关的教程中,我们将研究一些常见无源电路元件的阻抗,并绘制流过元件的电流和施加在其上的电压的相量图。交流阻力。
-
谈谈电路计算中的余弦形式、相量形式和复数形式的关系2015-01-01 25322
-
请问:容抗的复数表达式的问题2016-02-27 13449
-
第30章 复数FFT的实现2016-09-28 7630
-
请问C66x系列有没有专门的矩阵复数这一类的运算库?2018-07-24 1692
-
复数浮点FFT说明资料2021-08-10 879
-
计算器-复数的计算方法2016-03-22 1374
-
计算器复数运算方法2017-01-22 1242
-
DAC转换汇总资源下载2021-07-31 1069
-
为什么复数不能够排序?2023-04-18 1347
-
FPGA常用运算模块-复数乘法器2023-05-22 4102
-
实数混频和复数混频有什么差别?2023-10-31 2670
-
信道系数为什么是复数呢?单数可以吗?2023-11-03 2845
-
Python中如何表达复数2023-11-21 3362
-
复数中i在Python中如何定义2023-11-22 4574
全部0条评论

快来发表一下你的评论吧 !

