

正弦波形构造转换频率公式定义案例
描述
当电流流过导线或导体时,导线周围会产生一个圆形磁场,其强度与电流值有关。
如果移动此单线导体或者在固定磁场内旋转,由于导体通过磁通量的移动,在导体内感应出“EMF”,(电动势)。
从这里可以看出电力和磁力之间的关系给我们带来了,正如迈克尔法拉第发现“电磁感应”的效果,电机和发电机用来为我们的主电源产生正弦波形是这个基本原理。 / p>
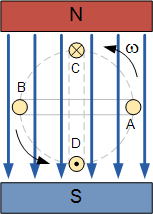
在电磁感应教程中,我们说过当单线导体穿过永久磁场从而切断其磁通线时,EMF然而,如果导体与t中的磁场平行移动,则会在其中感应出来。
在点 A 和 B 的情况下,没有切割磁通线并且没有EMF被感应到导体中,但是如果导体与磁场成直角移动,则在点 C 和 D 的情况下,切割最大磁通量,产生最大量的感应EMF。
此外,作为导体在 A 和 C ,0和90 o 之间的不同角度切割磁场,感应EMF的量将介于此零点之间和最大价值。然后,导体内感应的电动势的数量取决于导体与磁通量之间的角度以及磁场的强度。
交流发电机使用法拉第电磁感应的原理来转换机械能,如旋转,转换成电能,正弦波形。简单的发电机由一对永久磁铁组成,在北极和南极之间产生固定的磁场。在这个磁场内部是一个单一的矩形线圈,可以绕固定轴旋转,允许它以各种角度切割磁通量,如下所示。
基本单线圈交流发电机

当线圈围绕垂直于磁场的中心轴逆时针旋转时,线圈以不同角度切割在北极和南极之间设置的磁力线作为环路旋转。在任何时刻环路中感应EMF的量与线环的旋转角度成比例。
当线环旋转时,线中的电子围绕环绕一个方向流动。现在当导线环旋转超过180° o 点并沿相反方向的磁力线移动时,导线环中的电子改变并沿相反方向流动。然后电子运动的方向决定了感应电压的极性。
因此我们可以看到,当环路或线圈物理旋转一整圈或360 o 时,对于线圈的每次旋转产生一个波形周期产生完整的正弦波形。当线圈在磁场内旋转时,通过碳刷和滑环对线圈进行电连接,滑环用于传递线圈中感应的电流。
EMF的数量诱导成线圈切割磁力线由以下三个因素决定:
速度 - 速度线圈在磁场内旋转。
强度 - 磁场强度。
Length - 通过磁场的线圈或导体的长度。
我们知道电源的频率是一个周期出现的次数第二,该频率以赫兹为单位。如上所示,通过包括北极和南极的磁场,线圈的每次完整旋转产生一个感应电动势循环,如果线圈以恒定速度旋转,则每秒产生恒定数量的循环,给出恒定的频率。因此,通过增加线圈的旋转速度,频率也将增加。因此,频率与旋转速度成正比(ƒαN),其中Ν= rpm
此外,我们上面的简单单线圈发电机只有两个极点,一个是北极,一个南极,只给出一对极。如果我们在发电机上面增加更多的磁极,使其现在总共有四个极,两个北极和两个南极,那么对于线圈的每次旋转,将产生两个相同转速的循环。因此,频率与发电机的磁极对数(ƒαP)成正比,其中P =“极对数”。
然后从这两个事实我们可以说AC发电机的频率输出是:

其中: N 是旋转速度inr.p.m. P 是“极对”的数量,60将其转换为秒。
瞬时电压
在任何时刻线圈中感应的EMF时间取决于线圈切断磁极之间的磁通线的速率或速度,这取决于发电装置的旋转角度θ(θ)。由于交流波形不断改变其值或幅度,因此任何时刻的波形将具有与下一时刻不同的值。
例如,1ms处的值将与值在1.2ms等等。这些值通常称为瞬时值,或 V i 然后波形的瞬时值及其方向将根据线圈在磁场中的位置如下图所示。
磁场内磁场的位移

正弦波形的瞬时值作为“瞬时值=最大值xsinθ”给出,这由公式推广。

其中, V max 是线圈中感应的最大电压,θ=ωt,是旋转角度线圈相对于时间。
如果我们知道波形的最大值或峰值,通过使用上面的公式,可以计算沿波形的各个点的瞬时值。通过将这些值绘制到方格纸上,可以构建正弦波形。
为了简单起见,我们将绘制每45 o V MAX 值为100V。以较短的间隔绘制瞬时值,例如每30 o (12点)或10 o (36点),将产生更准确的正弦波形结构。
正弦波形构造


正弦波形上的点是通过投影获得的在0 o 和360 o 到波形的纵坐标,对应于角度θ,当线圈或线圈旋转一整圈,或360 o 时,产生完整波形。
从正弦波形图可以看出,当θ等于0 o 时,180 o 或360 o ,生成的EMF为零,因为线圈切割最小量的通量线。但当θ等于90 o 且270 o 时,生成的EMF处于其最大值,因为最大通量量被切断。 / p>
因此,正弦波形在90 o 处具有正峰值,在270 o 处具有负峰值。位置 B,D,F 和 H 生成与公式对应的EMF值: e =Vmax.sinθ。
然后我们的简单单回路发生器产生的波形形状通常被称为正弦波,因为据说它的形状是正弦波。这种类型的波形称为正弦波,因为它基于数学中使用的三角正弦函数( x(t)=Amax.sinθ)。
处理时在时域中的正弦波,尤其是与电流相关的正弦波,沿波形的水平轴使用的测量单位可以是时间,度或弧度。在电气工程中,更常见的是使用Radian作为沿水平轴而不是角度的角度的角度测量。例如,ω = 100rad / s,或500rad / s。
Radians
Radian,(rad)在数学上被定义为圆的象限,其中圆周上的距离等于圆的长度。同一圆的半径( r )。由于圆的圆周等于2πxradius,因此在圆的360 o 周围必须有2π弧度。
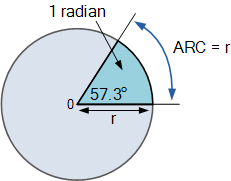
<换句话说,弧度是角度测量的单位,一个弧度(r)的长度将围绕圆的整个圆周拟合6.284(2 *π)倍。因此,一个弧度等于360 o /2π=57.3 o。在电气工程中,使用弧度非常常见,因此记住以下公式非常重要。
Radian的定义

使用弧度作为正弦波形的测量单位,可以得到2π弧度循环360 o 。那么一半的正弦波形必须等于1π弧度或者只是π(pi)。然后知道pi,(π)等于 3.142 ,因此正弦波形的度和弧度之间的关系如下:
关系在度和弧度之间

将这两个方程应用于波形上的各个点给我们。

下表给出了正弦分析中使用的更常见等效物的度数和弧度之间的转换。
度数和弧度之间的关系

发电机围绕其中心轴旋转的速度决定了正弦波形的频率。由于波形的频率为 f Hz或每秒周期,波形也具有角频率,ω,(希腊字母omega),以弧度/秒为单位。然后正弦波形的角速度给出为。
正弦波形的角速度

并且在英国,主电源的角速度或频率如下:

在美国作为他们的主电源频率为60Hz,可以给出: 377 rad / s
所以我们现在知道发电机围绕其中心轴旋转的速度决定了频率。正弦波形,也可以称为角速度,ω。但我们现在也应该知道完成一整圈所需的时间等于正弦波的周期时间( T )。
因为频率成反比因此,对于它的时间段,ƒ= 1 / T 我们可以用上面等式中的频率数量代替等效的周期时间量而代以给我们。

上述等式表明,对于正弦波形的较小周期时间,波形的角速度必须越大。同样在上面对于频率量的等式中,频率越高,角速度越高。
正弦波形示例No1
正弦波形定义为: V m = 169.8sin(377t)伏。在6毫秒(6ms)的时间后,计算波形的RMS电压,其频率和电压的瞬时值(V i 。)
我们从上面知道给出正弦波形的一般表达式是:

然后将它与我们给定的正弦波表达式进行比较 V m = 169.8sin(377t)以上的波形将为波形提供 169.8 伏的峰值电压值。
波形RMS电压计算如下:
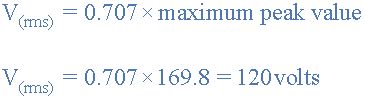
角速度(ω)以377 rad / s给出。然后2πƒ= 377 。所以波形的频率计算如下:

瞬时电压<在6mS的时间后,span> V i 的值为:

请注意,时间 t = 6mS 时的角速度以弧度(rads)给出。如果愿意,我们可以将其转换为等效角度,并使用该值代替计算瞬时电压值。因此,瞬时电压值的角度为:

正弦波形
然后使用广义格式用于分析和计算正弦波形的各种值如下:
正弦波形
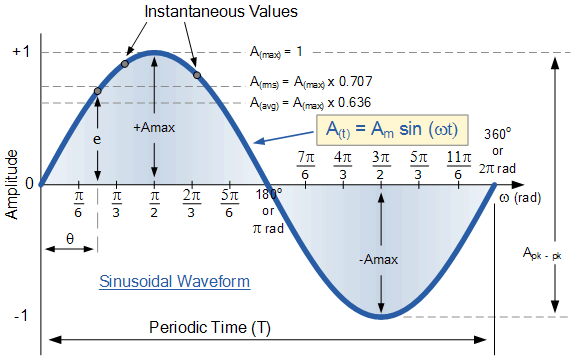
在下一个关于相位差的教程中,我们将研究两个具有相同频率但在不同时间间隔通过水平零轴的正弦波形之间的关系。
-
电源技术之正弦波形(一)2020-09-18 0
-
电源技术之正弦波形(二)2020-09-18 0
-
RC正弦波发生器及波形变换2009-03-17 9766
-
三相T/6正弦波形发生器电路图2009-07-17 2405
-
正弦波是什么,正弦波简介2010-04-15 24957
-
把三角波转换成正弦波的宽带正弦波转换器2010-05-06 7656
-
数字正弦波形产生的数学推导2011-05-24 824
-
Labview之不同扫描方式显示正弦波形2016-04-19 688
-
什么是正弦波逆变器_正弦波逆变器的工作原理及相关电路图2017-11-20 87539
-
单片机课设波形发生器 产生方波、三角波、正弦波、锯齿波 波形幅度可调、频率可调2021-11-15 2167
-
有源晶振的波形是正弦波吗?怎么测量?2023-04-17 2672
-
纯正弦波逆变器和修正弦波逆变器的区别2024-01-23 7669
-
振荡电路为什么能产生正弦波?正弦波振荡电路的振荡条件2024-04-04 3230
-
示波器测量正弦波波形的基本步骤2024-05-27 2979
-
正弦波逆变器的定义和基本结构2024-10-05 589
全部0条评论

快来发表一下你的评论吧 !

