有源带通滤波器电路频率案例

带通滤波器或任何滤波器的主要特性是它能够在指定频段或称为“通带”的频率范围内传递相对无衰减的频率。

对于低通滤波器，该通带从0Hz或DC开始，并继续向上到指定的截止频率点，距离最大通带增益-3dB。同样，对于高通滤波器，通带从-3dB截止频率开始，并继续向无穷大或有源滤波器的最大开环增益。

然而，有源频段通过滤波器略有不同，因为它是一个用于电子系统的频率选择滤波器电路，用于分离一个特定频率的信号，或一系列信号，这些信号位于信号的某个“频带”范围内其他频率。该频段或频率范围设置在标记为“较低频率”（ƒ L ）和“较高频率”（ƒ H ）同时衰减这两点之外的任何信号。

简单的有源带通滤波器可以通过级联轻松实现如图所示，一个低通滤波器与一个高通滤波器一起使用。

截止或转角低通滤波器（LPF）的频率高于高通滤波器（HPF）的截止频率，-3dB点的频率之差将决定带通滤波器的“带宽”，同时衰减任何频率。这些点之外的信号。制作非常简单的有源带通滤波器的一种方法是将我们先前看到的基本无源高通和低通滤波器连接到放大运算放大器电路，如图所示。

有源带通滤波器电路

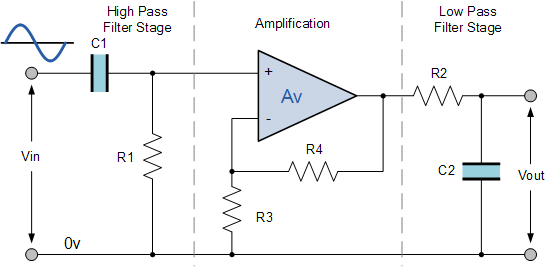
将各个低通和高通无源滤波器级联在一起产生低电平“ Q因子“型滤波器电路，具有宽通带。滤波器的第一级将是高通级，使用电容器阻止来自源的任何DC偏置。这种设计的优点是产生相对平坦的不对称通带频率响应，其中一半表示低通响应，另一半表示高通响应，如图所示。

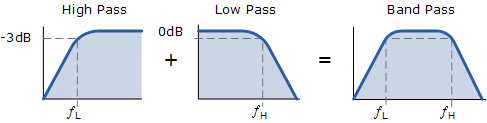
较高的角点（ƒ H ）以及较低的转角频率截止点（ ƒ L ）在标准的一阶低通和高通滤波器电路中计算与之前相同。显然，在两个截止点之间需要合理的分离，以防止低通和高通阶段之间的任何相互作用。放大器还提供两级之间的隔离，并定义电路的整体电压增益。

因此，滤波器的带宽是这些上下-3dB点之间的差值。例如，假设我们有一个带通滤波器，其-3dB截止点设置为200Hz和600Hz。然后滤波器的带宽如下：带宽（BW）= 600 - 200 = 400Hz。

有源带通滤波器的归一化频率响应和相移如下：

有源带通频率响应

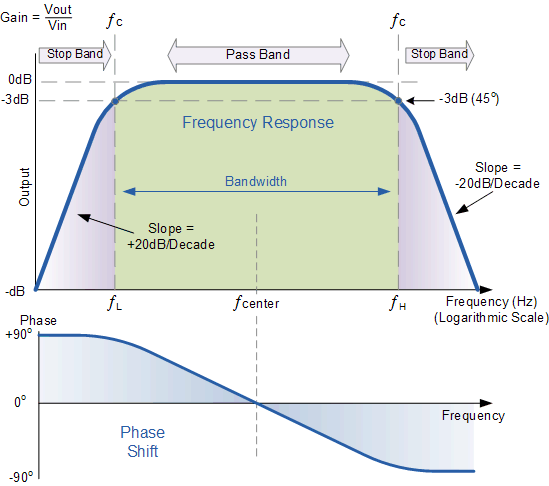
虽然上述无源调谐滤波器电路可用作波段通过滤波器，通带（带宽）可能相当宽，如果我们想要隔离一小段频率，这可能是一个问题。有源带通滤波器也可以使用反相运算放大器制作。

因此，通过重新排列滤波器内电阻器和电容器的位置，我们可以产生更好的滤波器电路，如下所示。对于有源带通滤波器，下限截止-3dB点由ƒ C1 给出，而上截止-3dB点由ƒ给出<子> C2 。

反向带通滤波器电路

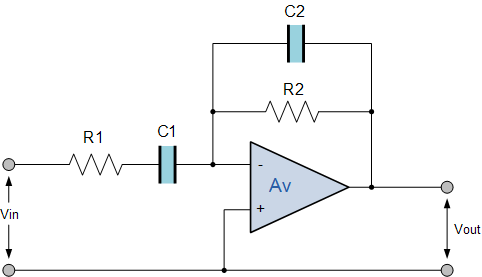
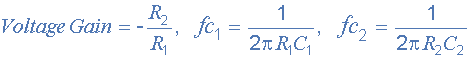
这种类型的带通滤波器设计为具有更窄的通带。滤波器的中心频率和带宽与 R1，R2，C1 和 C2 的值相关。滤波器的输出再次来自运算放大器的输出。

多反馈带通有源滤波器

我们可以通过重新排列来改善上述电路的带通响应这些组件再次产生无限增益多反馈（IGMF）带通滤波器。这种类型的有源带通设计产生一个基于负反馈有源滤波器的“调谐”电路，使其具有高“Q因子”（高达25）的幅度响应和在其中心频率两侧的急剧滚降。由于电路的频率响应类似于谐振电路，因此该中心频率称为谐振频率（ƒr）。考虑下面的电路。

无限增益多反馈有源滤波器

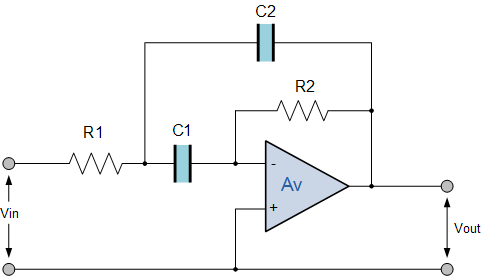
此有效频段通过滤波器电路使用运算放大器的全增益，通过电阻器施加多个负反馈， R 2 和电容器 C 2 。然后我们可以定义IGMF过滤器的特征如下：

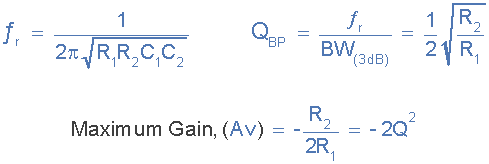
我们可以看到之间的关系电阻， R 1 和 R 2 确定带通“Q因子”和频率发生最大幅度时，电路的增益将等于 -2Q 2 。然后随着增益的增加，选择性也随之增加。换句话说，高增益 - 高选择性。

有源带通滤波器示例No1

有源带通滤波器，其电压增益 Av 为1 （1）使用无限增益多反馈滤波器电路构建1kHz的谐振频率ƒr。计算实现电路所需元件的值。

首先，我们可以确定两个电阻的值， R 1 和 R 2 有源滤波器需要使用电路增益来查找 Q ，如下所示。

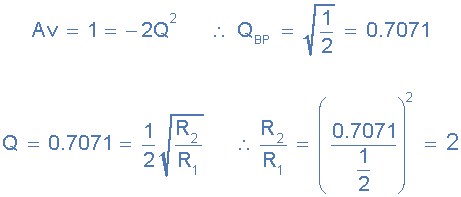
然后我们可以看到 Q = 0.7071 的值给出了电阻关系， R 2 是电阻 R 1 的两倍。然后我们可以选择任何合适的阻力值来给出所需的两个比率。然后电阻 R 1 =10kΩ且 R 2 =20kΩ。

中心或谐振频率为1kHz。使用获得的新电阻值，我们可以确定所需的电容值，假设 C = C 1 = C 2 。

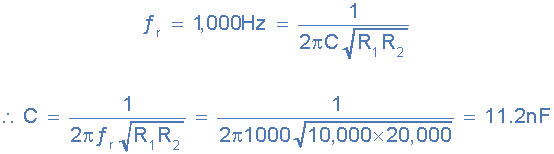
最接近的标准值是 10nF 。

谐振频率点

任何无源或有源带通滤波器的频率响应曲线的实际形状将取决于滤波器电路的特性，上面的曲线被定义为“理想”频带通过回应。有源带通滤波器是二阶型滤波器，因为它的电路设计中有“两个”无功分量（两个电容）。

由于这两个无功分量，滤波器的“中心频率”，ƒc将具有峰值响应或谐振频率（ƒr）。中心频率通常计算为上下截止点之间的两个-3dB频率的几何平均值，谐振频率（振荡点）如下：

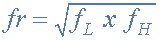
其中：

ƒ r 是共振或中心频率

ƒ L 是-3dB的截止频率点

ƒ H 是上-3db截止频率点

在我们上面的文本中的简单示例中，滤波器的上下-3dB截止点是在200Hz和600Hz分别，有源带通滤波器的谐振中心频率为：

“Q”或品质因数

在带通滤波器电路中，滤波器上下-3dB角点之间的实际通带的总宽度决定了品质因数或Q-point电路。该Q因子是对带通滤波器的“选择性”或“非选择性”如何朝向给定的频率扩展的度量。 Q因子的值越低，滤波器的带宽越宽，因此Q因子越高，滤波器越窄，“选择性”越大。

品质因数，Q <过滤器的/ b>有时会被赋予希腊符号Alpha，（α）并被称为alpha-peak frequency，其中：

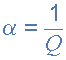
由于有源带通滤波器（二阶系统）的品质因数与“锐度”有关“滤波器响应其中心谐振频率（ƒr），它也可以被认为是”阻尼系数“或”阻尼系数“，因为滤波器具有更强的阻尼，它的响应更为平坦。同样，过滤器的阻尼越小，其响应越敏锐。阻尼比为希腊符号Xi，（ξ）其中：

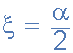
带通滤波器的“Q”是谐振频率，（ƒr）与带宽<的比率/ b>，（ BW ）在上下-3dB频率之间，并给出如下：

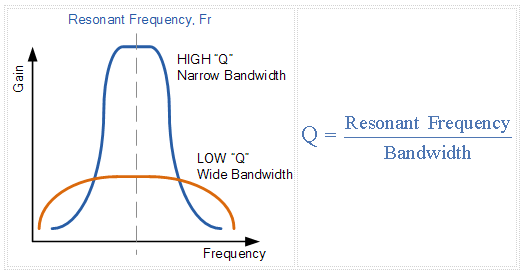
然后为我们在带通滤波器的品质因数“Q”之上的简单示例如下：

346Hz / 400Hz =0.865。请注意，Q是一个比率且没有单位。

在分析有源滤波器时，通常会考虑归一化电路，它产生具有矩形形状的“理想”频率响应，并且通带和阻带之间的过渡，具有突然或非常陡峭的滚降斜率。然而，这些理想的响应在现实世界中是不可能的，因此我们使用近似来为我们设计的滤波器类型提供最佳的频率响应。

可能是最好的滤波器近似值这是Butterworth或最大平坦的响应滤波器。在下一个教程中，我们将研究更高阶的滤波器，并使用巴特沃斯近似来产生滤波器，其频率响应与通带中的数学上一样平坦，并具有平滑的过渡或滚降速率。