

Sallen和Key过滤器电路分压器及函数方程案例
描述
Sallen-Key滤波器拓扑用作实现更高阶有源滤波器的构建块
Sallen和Key Filter设计是一个二阶有源滤波器拓扑,我们可以用作实现高阶滤波器电路的基本构建模块,如低通滤波器(LPF),高通滤波器(HPF)和带通滤波器电路。
As我们已经在这个滤波器部分看到,无源或有源电子滤波器用于仅在有限频率范围内需要信号幅度的电路中。使用 Sallen-Key滤波器设计的优势在于它们易于实现和理解。
Sallen和Key拓扑是一种基于单个非反相的有源滤波器设计运算放大器和两个电阻,从而创建一个压控电压源(VCVS)设计,具有滤波器特性,高输入阻抗,低输出阻抗和良好的稳定性,因此允许单独的Sallen键滤波器部分级联到一起产生更高阶的滤波器。
但在我们看一下 Sallen-key滤波器的设计和操作之前,让我们首先提醒自己一个电阻器 - 电容器的特性,当受到一系列输入频率时,RC网络或RC网络。
分压器
当两个(或更多)电阻器在一个直流电源电压上连接在一起时,不同的电压值将是在每个电阻器上产生,产生基本上称为分压器或压电器的电阻器分压器网络。
电阻分压器
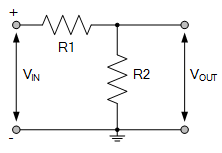
所示基本电路由两个串联电阻串联电压, V IN 。
欧姆定律告诉我们电阻上的电压降是电流的总和流经它的电阻值乘以电阻值V = I * R,所以如果两个电阻相等,那么两个电阻上的电压下降, R1 和 R2 也会在电阻 R2 之间产生或下降的电压代表输出电压, V OUT
span>由两个电阻和输入电压的比值给出。因此,这个简单的分压器网络的传递函数如下:
电阻分压器传递函数

但是如果我们将输入电压改为交流电源或信号并改变其频率范围,输出电压 V OUT 会发生什么。实际上没什么,因为电阻通常不受频率变化(排除线绕)的影响,因此它们的频率响应为零,允许AC,Irms 2 * R电压在电阻器上产生或下降与稳态直流电压相同。
RC分压器
如果我们将电阻器 R1 更改为电容器, C 如图所示,这将如何影响我们之前的传递函数。我们从有关电容器的教程中了解到,当连接到直流电源时,电容的行为就像开路一样。
RC分压器

因此,当稳态直流电源连接到 V IN 时,电容器将在5个时间常数(5T = 5RC)后充满电,在这段时间内,它不会从电源中吸取电流。因此没有电流流过电阻器 R 并且没有电压降产生,因此没有输出电压。换句话说,电容器一旦充电就会阻止稳态直流电压。
如果我们现在将输入电源改为交流正弦电压,这个简单的RC电路的特性会完全随着直流或恒定部分而变化。信号被阻止。所以现在我们正在分析频域中的RC电路,这是信号中依赖于时间的部分。
在交流电路中,电容具有容抗电容电抗
b>,X C但我们仍然可以用与电阻电路相同的方式分析RC电路,区别在于电容器的阻抗现在取决于频率。
对于交流电路和信号,容抗( X C ),是对交替的反对电流以欧姆为单位流过电容器。电容电抗是频率相关的,即在低频率(ƒ≅0)时电容表现得像开路并阻塞它们
在非常高的频率(ƒ≅∞)下,电容表现得像一个短路,并将信号直接传递给输出,因为 V OUT = V <子> IN 。然而,在这两个极端频率之间的某处,电容器具有由 X C 给出的阻抗。所以我们的上面的分压器传递函数变为:

因此频率的变化会导致的变化X C ,这会导致输出电压幅度的变化。考虑下面的电路。
RC滤波电路

图表显示了频率响应这个简单的1 st - 阶RC电路。在低频时,电压增益非常低,因为输入信号被电容器的电抗阻挡。在高频时,电压增益很高(单位),因为电抗会使电容器有效地成为这些高频的短路,因此 V OUT = V IN
然而,变频器的电抗等于电阻的电阻的频率点,即: X C = R ,这称为“临界频率”点,或更常称为截止频率,或转角频率ƒ C。
当 X C = R时发生截止频率用于计算此临界频率点的标准公式如下:
截止频率方程

截止频率ƒ C 定义电路在此示例中从衰减或阻塞以下所有频率的位置变化, ƒ C 并开始通过所有频率ab ove ƒ C 点。因此,该电路称为“高通滤波器”。
截止频率是输入到输出信号的比值为0.707,当转换为分贝时等于 - 3分贝。这通常被称为滤波器3dB下降点。
由于电容器的电抗与频率有关,即容抗( X C )与施加的频率成反比,我们可以修改上面的分压器方程,得到这个简单的RC高通滤波器电路的传递函数,如图所示。
RC滤波电路
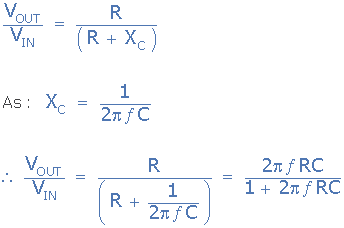
RC滤波器的一个主要缺点是输出幅度总是小于输入,所以它永远不会大于1 。此外,更多RC级或电路对输出的外部负载将对滤波器特性产生影响。解决此问题的一种方法是通过在基本RC配置中添加运算放大器将无源RC滤波器转换为“有源RC滤波器”。
通过添加运算放大器,基本RC滤波器可以是设计用于在其输出端提供所需的电压增益,从而将滤波器从衰减器改变为放大器。此外,由于运算放大器的高输入阻抗和低输出阻抗,可以防止滤波器的外部负载,从而可以在很宽的频率范围内轻松调节,而不会改变设计的频率响应。
考虑简单的有源下面的RC高通滤波器。
有源高通滤波器

RC滤波器电路的一部分响应与上述相同,即通过高频但阻挡低频,截止频率由R和C的值设定。运算放大器或简称运算放大器配置为非反相放大器,其电压增益由两个电阻的比率设定, R 1 和 R 2 。
然后非反相运算放大器的通带中的闭环电压增益 A V 为:
截止频率方程

RC滤波器示例No1
A简单的1 st 阶有源高通滤波器要求截止频率为500Hz,通带增益为9dB。假设使用标准的741运算放大器,计算所需的元件。
从上面我们已经看到截止频率ƒ C 被确定通过频率选择RC电路中的 R 和 C 的值。如果我们假设 R 的值为5kΩ(任何合理的值都可以),那么 C 的值计算如下:

C 的计算值为63.65nF,因此最接近的首选值为62nF。
通带区域中高通滤波器的增益为+ 9dB,相当于电压增益, A V 为2.83。假设反馈电阻的任意值, R 1 为15kΩ,这给出了电阻 R 1 的值:

R 2 的计算值>是8197Ω。最接近的优选值为8200Ω或8.2kΩ。然后,这为我们的有源高通滤波器示例提供了最终电路:
高通滤波器电路

我们已经看到,可以使用单个电阻和电容产生一个简单的一阶高通滤波器,产生一个截止频率ƒ C 输出幅度从输入幅度向下-3dB的点。通过向第一个RC滤波器级添加第二个RC滤波器级,我们可以将电路转换为二阶高通滤波器。
二阶RC滤波器
最简单的二阶RC滤波器由两个RC部分组成,如图所示。但是,为了使这种基本配置正常工作,两个RC级的输入和输出阻抗不应影响彼此的操作,即它们应该是非相互作用的。
高通滤波器电路
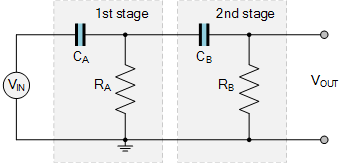
将一个RC滤波器级与另一个(相同或不同的RC值)级联,因为每个连续阶段都不能很好地工作加载前一个RC级,当添加更多RC级时,截止频率点进一步远离设计或要求的频率。
克服无源滤波器设计这个问题的一种方法是使用第二RC级的输入阻抗至少比第一RC级的输出阻抗大10倍。即 R B = 10 * R 1 和 C B = C A / 10 在截止频率处。
将元件值增加10倍的优点是得到的二阶滤波器产生更陡峭的滚降比级联RC级40dB /十倍。但是如果你想设计一个4 th 或6 th -order过滤器,那么计算十倍于前面组件的值可能是耗时且复杂的。
将RC过滤器级联在一起的一种简单方法,它们不相互作用或相互加载以创建更高阶的过滤器(各个过滤器部分不必相同),可以轻松调整和设计以提供所需的电压增益是使用 Sallen-key Filter 阶段。
Sallen和Key Filters
Sallen-Key是设计一阶(1 st -order)的最常见过滤器配置之一和二阶(2 nd - 阶)滤波器,因此用作创建更高阶滤波器的基本构建块。
Sallen-key的主要优点过滤器设计是:
简洁和理解他们的基本设计
使用非反相用于提高电压增益的放大器
一阶和二阶滤波器设计可以轻松级联在一起
低通和高通阶段可以一起级联
每个RC级可以有不同的电压增益
RC组件和放大器的复制
二阶Sallen-key平台比级联RC具有陡峭的40dB /十倍滚降
然而,基本Sallen-key滤波器存在一些限制设计的原因是电压增益 A V 和放大系数 Q 由于在Sallen中使用运算放大器而密切相关关键设计。几乎任何大于0.5的 Q 值都可以实现,因为使用非反相配置,电压增益 A V 将始终大于1,(单位)但必须小于3否则会变得不稳定。
最简单的Sallen-key滤波器设计形式是使用相等的电容和电阻值(但C和R不是必须相等),运算放大器配置为单位增益缓冲器,如图所示。请注意,电容 R A 不再接地,而是为放大器提供正反馈路径。
Sallen-key高通滤波器电路

被动组件 C A , R A , C B 和 R B 形式二阶频率选择电路。因此,在低频时,电容 C A 和 C B 显示为开路,因此输入信号被阻塞导致无输出。在较高频率下, C A 和 C B 在正弦输入信号中显示为短路,因此信号直接缓冲到输出。
但是,在截止频率点附近, C A 和 C B 与 R A 和 R B 的值相同,如上所述,通过 C B 产生的正反馈提供电压增益,并增加输出信号放大率, Q 。
由于我们现在有两组RC网络,Sallen-Key滤波器的截止频率的上述公式也被修改:
Sallen-key截止频率方程

如果两个串联电容 C A 且 C B 相等( C A = C B = C )和两个电阻器 R A 和 R B 也相等( R A = R B = R ),然后上面的等式简化为原始截止频率方程:
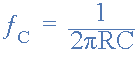
由于运算放大器配置为单位增益缓冲器,即 A = 1 ,截止频率ƒ C 和 Q 完全相互独立,从而实现更简单的滤波器设计。然后放大系数 Q 计算如下:
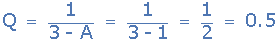
因此对于统一-gain缓冲器配置,滤波器电路的电压增益( A V )在截止频率点等于0.5或-6dB(过阻尼),我们希望看到这个,因为它是一个二阶滤波器响应,为0.7071 * 0.7071 = 0.5。那就是-3dB * -3dB = -6dB。
然而,由于 Q 的值决定了滤波器的响应特性,正确选择了运算放大器的两个反馈电阻, R 1 和 R 2 ,允许我们选择所需的通带增益 A 对于选定的放大系数, Q 。
请注意,对于Sallen-key滤波器拓扑,选择 A 的值非常接近最大值3将导致高 Q 值。高 Q 将使滤波器设计对反馈电阻 R 1 和 R 2的容差变化敏感 。例如,将电压增益设置为2.9(A = 2.9)将导致 Q 的值为10(1 /(3-2.9)),因此滤波器在周围变得非常敏感ƒ C 。
Sallen-key Filter Response

然后我们可以看到 Q 的值越低,Sallen和Key滤波器设计就越稳定。虽然 Q 的高值会使设计不稳定,但是增益非常高会产生负 Q 会导致振荡。
Sallen和Key Filter示例No2
设计具有以下特征的二阶高通 Sallen和Key Filter 电路:ƒ C = 200Hz 和 Q = 3
为了简化数学运算,我们假设两个串联电容 C A 和 C B 相等( C A = C B = C )并且两个电阻 R A 和 R B 相等( R A = R <子>乙 = R )
R 的计算值为7957Ω,因此最接近的首选值为8kΩ。
对于 Q = 3 ,增益计算如下:

如果 A = 2.667 ,那么 R 1 / R <子> 2 = 1.667 如图所示。

R 2的计算值 为5998Ω,因此最接近的首选值使用6000Ω或6kΩ。然后,这为我们的Sallen和Key高通滤波器示例提供了最终电路:
Sallen和Key High Pass滤波器

然后截止或转角频率为200Hz,通带增益为2.667,截止频率为8(2.667 * 3)时的最大电压增益= 3,我们可以在下面的Bode图中显示这个二阶高通Sallen和Key滤波器的特征。
Sallen和Key Filter Bode Plot

Sallen和Key Filter Summary
我们在本教程中已经看到Sallen-Key配置,也称为电压控制,电压源(VCVS)电路是最广泛使用的滤波器拓扑结构,主要是因为其设计中使用的运算放大器可配置为单位增益缓冲器或非反相放大器。
基本的Sallen-key滤波器配置可用于实现不同的滤波器响应,例如,Butterworth, Chebyshev,或贝塞尔正确选择RC滤波器网络。可以使用 R 和 C 的大多数实际值,记住对于特定的截止频率点, R 和的值R 成反比。也就是说, R 的值变小, C 变大,反之亦然。
Sallen-key是2 nd - 阶滤波器设计,可以与其他RC阶段级联,以创建更高阶的滤波器。多个滤波器级不需要相同,但可以各自具有不同的截止频率或增益特性。例如,将低通阶段和高通阶段组合在一起以创建Sallen和Key带通滤波器。
这里我们研究设计一个Sallen-key高通滤波器,但同样的规则同样适用于低通设计。电压增益 A V 决定其响应并由分压电阻设置, R 1 和 R 2 记住电压增益必须小于3否则,滤波器电路将变得不稳定。
-
煤矿用过滤器滤芯2011-03-13 3409
-
elektrogas过滤器成都总代理2018-07-12 1327
-
过滤组、过滤器编号介绍2021-08-20 1336
-
CN过滤器原理2010-02-25 1389
-
过滤器的作用2018-12-12 49804
-
解密高效空气过滤器的性能及要求2020-03-19 2354
-
负压吸引系统过滤器的详细介绍2022-04-16 2280
-
丝扣Y过滤器2022-08-13 4657
-
丝扣Y过滤器及过滤器测试原理简介2022-09-05 3074
-
丝扣Y形过滤器2022-10-24 4428
-
Y型过滤器2022-10-25 3531
-
汉克森过滤器系列介绍2023-03-01 1609
-
过滤器药液过滤器滤除率测试仪2023-03-09 1528
-
杀菌过滤器 灭菌过滤器 除菌过滤器2022-03-03 3679
-
springboot过滤器和拦截器哪个先执行2023-12-03 3309
全部0条评论

快来发表一下你的评论吧 !

