

带阻滤波器响应配置特性和电路案例及设计方程案例摘要
描述
一个称为陷波滤波器的阻带滤波器阻止和拒绝位于其两个截止频率点之间的频率通过该范围任一侧的所有频率
通过组合具有RC高通滤波器的基本RC低通滤波器我们可以形成一个简单的带通滤波器,它将通过两个截止频率点两侧的频率范围或频带。但我们也可以将这些低通和高通滤波器部分结合起来,产生另一种称为带阻滤波器的RC滤波器网络,它可以阻止或至少严重衰减这两个截止频率点内的频带。
带阻滤波器,(BSF)是另一种频率选择电路,其功能与我们之前看到的带通滤波器完全相反。带阻滤波器,也称为带阻滤波器,通过所有频率,但指定阻带内的频率大大衰减。
如果此阻带是在几赫兹的非常窄且高度衰减的情况下,带阻滤波器通常被称为陷波滤波器,因为它的频率响应表明具有高选择性的深陷波(陡峭的一侧)此外,就像带通滤波器一样,带阻(带阻或陷波)滤波器是一个二阶(两极)滤波器,具有两个切口 - 而不是一个扁平的更宽的波段。
关闭频率,通常称为-3dB或半功率点,在这两个-3dB点之间产生较宽的阻带带宽。
然后带阻滤波器的功能过于通过所有这些频率从零开始(DC)直到其第一个(下部)截止频率点ƒ L ,并将所有这些频率超过其第二个(上部)截止频率 ƒ<苏b> H ,但阻止或拒绝其间的所有频率。然后滤波器带宽BW定义为:(ƒ H - ƒ L )。
因此,对于宽带带阻滤波器,滤波器实际阻带在其衰减时位于其低-3dB点和高-3dB点之间,或拒绝这两个截止频率之间的任何频率。因此,理想带阻滤波器的频率响应曲线如下:
带阻滤波器响应

从上面的带通电路的幅度和相位曲线可以看出,量ƒ L ,ƒ H 和ƒ C 与用于描述带通滤波器行为的那些相同。这是因为带阻滤波器只是标准带通滤波器的倒置或称赞形式。实际上,用于带宽,通带,阻带和中心频率的定义与以前相同,我们可以使用相同的公式来计算带宽, BW ,中心频率,ƒ C 和品质因数, Q 。
理想的带阻滤波器在其阻带中具有无限衰减,在任一通带中均具有零衰减。两个通带和阻带之间的过渡将是垂直的(砖墙)。有几种方法我们可以设计一个“带阻滤波器”,它们都可以达到同样的目的。
一般来说,带通滤波器是通过将低通滤波器(LPF)与高通滤波器相结合而构成的。通过过滤器(HPF)。如图所示,通过将“低通”和“高通”滤波器部分组合在一起形成带阻滤波器。
典型带阻滤波器配置
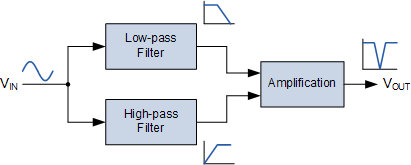
高通滤波器和低通滤波器的求和意味着它们的频率响应不会重叠,这与带通滤波器不同。这是因为它们的开始和结束频率处于不同的频率点。例如,假设我们有一个具有截止频率的一阶低通滤波器,与一阶高通并联的200Hz的ƒ L 滤波器的截止频率为ƒ H 为800Hz。由于两个滤波器有效并联连接,输入信号同时应用于两个滤波器,如上所示。
低于200Hz的所有输入频率都会通过低通滤波器无衰减地传递到输出端。同样,高于800Hz的所有输入频率都将通过高通滤波器无衰减地传递到输出。然而,输入信号频率介于200Hz和800Hz这两个频率截止点之间,即 f L 至 f H 。
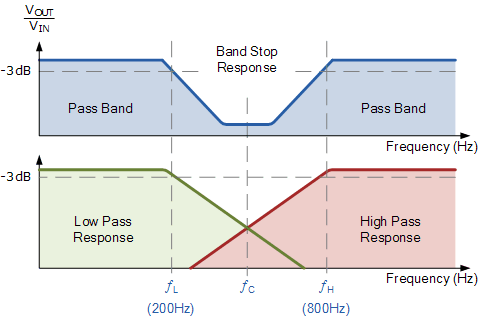
换句话说,频率为200Hz或更低且800Hz及以上的信号将不受影响但信号通过例如500Hz的频率将被拒绝,因为它太高而不能通过低通滤波器而太低而不能通过高通滤波器。我们可以在下面显示这个频率特性的影响。
带阻滤波器特性
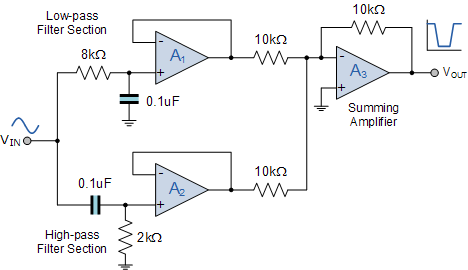
使用通过非反相电压跟随器彼此隔离的单个低通和高通滤波器电路,可轻松实现此滤波器特性的转换( Av = 1 )。然后使用连接为电压加法器(加法器)的第三运算放大器对这两个滤波器电路的输出求和。如图所示。
带阻滤波器电路
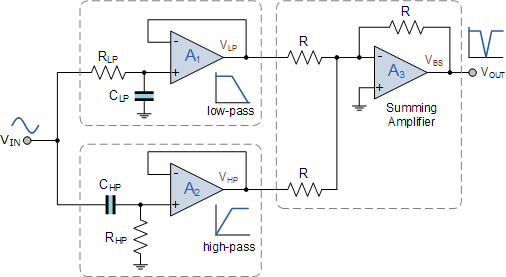
在带阻滤波器设计中使用运算放大器还允许我们将电压增益引入基本滤波器电路。通过添加输入和反馈电阻,可以轻松地将两个非反相电压跟随器转换为增益为 Av = 1 +Rƒ/ Rin 的基本同相放大器,如我们的非 - 反转运算放大器教程。
另外,如果我们要求带阻滤波器的-3dB截止点,例如1kHz和10kHz,以及介于-10dB之间的阻带增益,我们可以我们可以轻松设计出具有这些要求的低通滤波器和高通滤波器,并将它们级联在一起,形成我们的宽带带通滤波器设计。
现在我们了解了背后的原理带阻滤波器,让我们使用之前的截止频率值设计一个。
带阻滤波器示例No1
设计一个基本的宽带RC带阻滤波器的截止频率较低,频率为200Hz,截止频率较高,为800Hz。求出几何中心频率,-3dB带宽和电路Q.

带阻的上下截止频率点滤波器可以使用与低通滤波器和高通滤波器相同的公式,如图所示。
假设一个电容器,两个滤波器部分的 C 值为0.1uF,两个频率确定电阻的值 R L 和 R H 计算如下。
低通滤波器部分
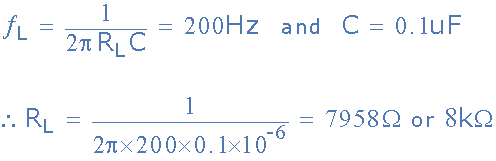
高通滤波器部分
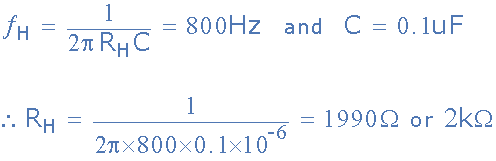
由此我们可以计算几何中心频率,ƒ C :
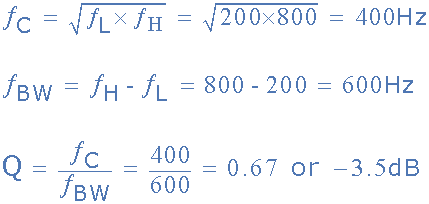
现在我们知道了两个滤波器级的元件值,我们可以将它们组合成一个单独的电压加法器电路来完成我们的滤波器设计。加法器输出的幅度和极性将在任何给定时间,即两个输入的代数和。
如果我们将运算放大器的反馈电阻和它的两个输入电阻设为相同的值,则说<跨度>10kΩ,然后反相求和电路将提供两个输入信号的数学正确和,电压增益为零。
然后我们的带阻(带阻)滤波器的最终电路例如:
带阻滤波器设计
我们已经看到,可以使用一阶或二阶低通和高通滤波器以及非反相求和运算放大器电路来制作简单的带阻滤波器,以抑制宽频带。但我们也可以设计和构建带阻滤波器,以产生更窄的频率响应,通过提高滤波器的选择性来消除特定频率。这种类型的滤波器设计称为“陷波滤波器”。
陷波滤波器
陷波滤波器是一种高选择性,高Q值的形式带阻滤波器,可用于抑制单个或非常小的频带而不是不同频率的整个带宽。例如,可能需要拒绝或衰减产生电噪声(如电源嗡嗡声)的特定频率,该电噪声已经从电感负载(如电机或镇流器照明)或谐波等的感应电路感应到电路中。
但除了滤波之外,音乐家还可以在音响设备中使用可变陷波滤波器,例如图形均衡器,合成器和电子分频器,以处理音乐声响应中的窄峰。然后我们可以看到陷波滤波器的使用方式与低通滤波器和高通滤波器的使用方式大致相同。
设计的陷波滤波器在其中心频率附近有一个非常窄且非常深的阻带。缺口的宽度由其选择性 Q 描述,与RLC电路中的谐振频率峰值完全相同。
最常见的陷波滤波器设计是双T陷波过滤网络。在它的基本形式中,双T,也称为并联三通,配置由两个T形截面形式的RC分支组成,它们使用三个电阻器和三个电容器,相对且相对的 R 如图所示,其设计的三通部分中的 C 元素,创造了更深的缺口。
基本的Twin-T陷波滤波器设计
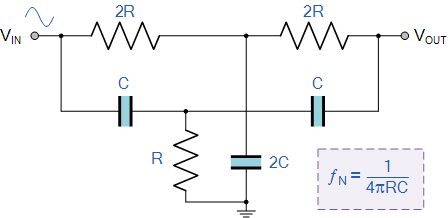
电阻 2R 和电容 2C 的上部T-pad配置形成低通滤波器设计的一部分,而电容 C 和电阻 R 的较低T-pad配置形成高通滤波器部分。这种基本的双T陷波滤波器设计提供最大衰减的频率称为“陷波频率”, f N ,其给出如下:
Twin-T陷波滤波器方程
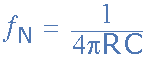
作为无源RC网络,这个基本双胞胎的缺点之一-T陷波滤波器的设计是,陷波频率以下的输出最大值( Vout )通常小于陷波频率以上的输出最大值,部分原因是两个串联电阻(<低通滤波器部分中的span> 2R ),其损耗大于高通部分中两个串联电容( C )的电抗。
除了陷波频率两侧的不均匀增益之外,该基本设计的另一个缺点是它具有0.25的固定 Q 值,大约为-12dB。这是因为在陷波频率下,两个串联电容的电抗等于两个串联电阻的电阻,导致每个支路中的电流异相180° o 。 / p>
我们可以通过使用连接到两个参考支路中心的正反馈来使陷波滤波器更具选择性来改善这一点。而不是将 R 和 2C 的连接点连接到地,(0v),而是将其连接到由输出信号供电的分压器网络的中心引脚,数量通过分压比设置的信号反馈确定 Q 的值,这反过来又在某种程度上决定了陷波的深度。
Single Op-放大器Twin-T陷波滤波器
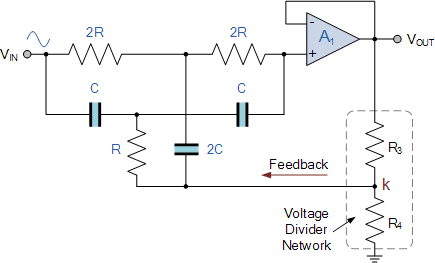
此处双T陷波滤波器部分的输出与单个非反相运算放大器缓冲器的分压器。分压器的输出反馈到 R 和 2C 的“接地”点。信号反馈量,称为反馈分数 k ,由电阻比设定,如下:
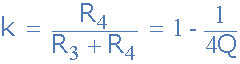
Q 的值由 R3 和 R4 电阻比确定,但如果我们想要使 Q 完全可调,我们可以用一个电位器替换这两个反馈电阻,并将其馈入另一个运算放大器缓冲器以增加负增益。此外,要获得给定频率下的最大陷波深度,可以消除电阻 R3 和 R4 ,并且 R 和的结点2C 直接连接到输出。
带阻滤波器示例No2
设计一个具有中心陷波频率的双运算放大器窄带RC陷波滤波器ƒ N 为1kHz,-3dB带宽为100 Hz。在您的设计中使用0.1uF电容,并以分贝计算预期的陷波深度。
给出的数据:ƒ N = 1000Hz , BW = 100Hz 和 C = 0.1uF 。
1。计算给定电容0.1uF的 R 值
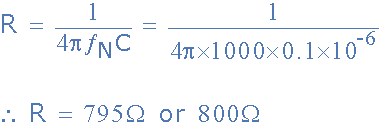
2。计算 Q的值
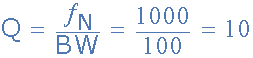
3。计算反馈分数的值 k
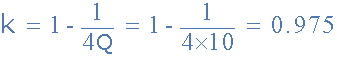
4。计算电阻 R3 和 R4
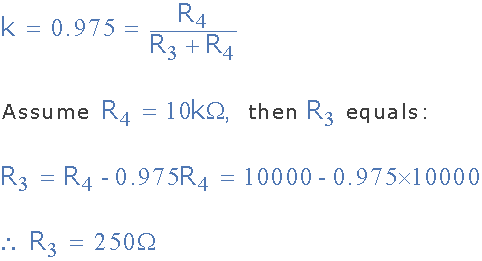
5。以分贝计算预期陷波深度, dB

陷波滤波器设计
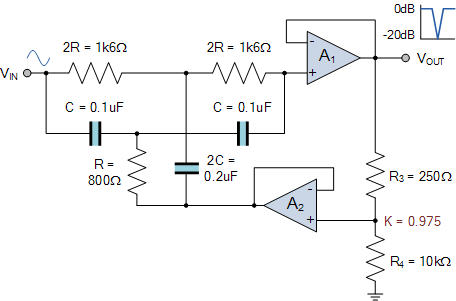
带阻滤波器摘要
我们在这里看到理想的带阻滤波器具有频率响应,该频率响应与带通滤波器。带阻滤波器阻止或“拒绝”位于其两个截止频率点之间的频率(ƒ L 和ƒ H )但是传递此范围两侧的所有频率。高于ƒ L 且低于ƒ H 的频率范围称为阻带。
带阻滤波器通过将高通的输出与低通滤波器的输出相加来实现这一点(特别是对于宽带设计),滤波器输出是差值。具有宽阻带的带阻滤波器设计也称为带阻滤波器,具有窄阻带的带阻滤波器设计称为陷波滤波器。无论哪种方式,带阻滤波器都是二阶滤波器。
陷波滤波器设计用于在单个频率附近提供高衰减,在所有其他频率上几乎没有衰减。陷波滤波器使用双T并联电阻 - 电容(RC)网络来获得深陷波。通过将一些输出反馈到两个三通的结点,可以获得更高的 Q 值。
使陷波滤波器更具选择性,并且可调节的值 Q ,我们可以将两个三通中的电阻和电容的连接点连接到连接到滤波器输出信号的分压器网络的中心点。正确设计的陷波滤波器可以在陷波频率下产生超过-60dB的衰减。
带阻滤波器在电子和通信电路中有很多用途,正如我们在这里看到的,它们可用于从系统中移除一段不需要的频率,允许其他频率以最小的损耗通过。陷波滤波器可以是高度选择性的,并且可以设计成抑制或衰减产生电噪声的特定频率或谐波含量,例如电路中的电源嗡嗡声。
-
陷波滤波器和带阻滤波器有什么联系,有什么区别2024-08-21 2460
-
带阻滤波器:原理、应用及性能分析?2023-12-11 2055
-
基于Matlab带阻滤波器电路设计2023-11-20 524
-
滤波器的特性 滤波器有哪些应用类型2023-02-24 5458
-
带阻滤波器和带通滤波器区别2023-02-15 8820
-
滤波器电路的理想幅频特性2020-06-24 4041
-
某新型带阻滤波器特性探究2017-11-09 1097
-
低功耗的带阻滤波器电路2009-12-07 1758
-
可变带阻滤波器电路图2009-06-25 725
-
带阻滤波器电路与幅频特性图2009-05-08 10026
-
Q值可调的带阻滤波器2009-04-15 849
-
带阻滤波器的设计2008-12-01 2386
-
无源带阻滤波器电路图,有源带阻滤波器原理图2008-09-24 28857
全部0条评论

快来发表一下你的评论吧 !

