二进制编码的十进制表示转换解码器

Binary Coded Decimal，或BCD，是将十进制数转换为二进制数的另一个过程

正如我们在教程的二进制数部分所看到的，使用了许多不同的二进制代码在数字和电子电路中，每个都有自己的特定用途。

由于我们自然生活在十进制（基数为10）的世界中，我们需要一些方法将这些十进制数转换为二进制数（base-2）计算机和数字电子设备理解的环境，以及二进制编码的十进制代码允许我们这样做。

我们之前已经看到，n位二进制代码是一组“n”位，假定为 2 n 1和0的不同组合。二进制编码十进制系统的优点是每个十进制数字由一组4个二进制数字或位表示，其方式与十六进制大致相同。因此，对于10位十进制数字（0到9），我们需要一个4位二进制代码。

但不要混淆，二进制编码的十进制不一样十六进制。而4位十六进制数有效至 F 16 表示二进制 1111 2 ，（十进制15） ，二进制编码的十进制数停在 9 二进制 1001 2 。这意味着虽然可以使用四个二进制数字表示16个数字（ 2 4 ），但在BCD编号系统中，六个二进制代码组合： 1010 （十进制10）， 1011 （十进制11）， 1100 （十进制12）， 1101 （十进制13）， 1110 （十进制14）和 1111 （十进制15）被归类为禁号，不能使用。

二进制编码小数的主要优点是它允许在decimal（base-10）和binary（base-2）表单之间轻松转换。但是，缺点是BCD代码是浪费的，因为不使用 1010 （十进制10）和 1111 （十进制15）之间的状态。然而，二进制编码的十进制有许多重要的应用，特别是使用数字显示。

在BCD编号系统中，十进制数被分成四位，用于数字中的每个十进制数字。每个十进制数字由其加权二进制值表示，执行数字的直接转换。因此，一个4位组表示每个显示的十进制数字，从 0000 表示零到 1001 表示九。

因此，例如，十进制的 357 10 （三百五十七）将以二进制编码的十进制表示为：

357 10 = 0011 0101 0111 （BCD）

然后我们可以看到BCD使用加权编码，因为每个4位组的二进制位表示最终值的给定权重。换句话说，BCD是加权代码，二进制编码十进制代码中使用的权重是 8 ， 4 ， 2 ， 1 ，通常称为8421代码，因为它形成相关十进制数字的4位二进制表示。

十进制数字的二进制编码十进制表示

h3>

Binary Power	2 3	2 2	2 1	2 0
二进制重量：	8	4	2	1

 

左边每个十进制数的十进制重量增加10倍。在BCD数字系统中，每个数字的二进制权重增加 2 如图所示。然后第一个数字的权重为 1 （ 2 0 ），第二个数字的权重为 2 （ 2 1 ），第三个是 4 的重量（ 2 2 ） ，第四个权重 8 （ 2 3 ）。

然后是十进制（denary）数字与加权二进制编码的十进制数字如下所示。

二进制编码十进制的真值表

然后我们可以看到8421 BCD代码只不过是每个二进制数字的权重，每个十进制（denary）数字表示为其四位纯二进制数。

十进制到BCD转换

正如我们上面所看到的，十进制到二进制编码十进制的转换非常类似于十六进制到二进制的转换。首先，将十进制数字分成加权数字，然后记下表示每个十进制数字的等效4位8421 BCD代码，如图所示。

二进制编码十进制示例No1

使用在上表中，将以下十进制（denary）数字转换为：85 10 ，572 10 和8579 10 到它们的8421 BCD等价物中。

85 10 = 1000 0101 （BCD）

572 10 = 0101 0111 0010 （BCD）

8579 10 = 1000 0101 0111 1001 （BCD）

请注意生成的二进制数后转换将是十进制数字的真正二进制转换。这是因为二进制代码转换为真正的二进制计数。

BCD到十进制转换

从二进制编码的十进制到十进制的转换与上面的完全相反。只需将二进制数分成四位数组，从最低有效位开始，然后写入每个4位组所代表的十进制数。如果需要生成完整的4位分组，最后添加额外的零。例如， 110101 2 将变为： 0011 0101 2 或 35 10 十进制。

二进制编码的十进制示例No2

转换以下二进制数：1001 2 ，1010 2 ，1000111 2 和10100111000.101 2 到它们的十进制等值中。

1001 2 = 1001 BCD = 9 10

1010 2 = 这会产生错误，因为它是十进制 10 10 且不是有效的BCD编号

1000111 2 = 0100 0111 BCD = 47 10

10100111000.101 2 = 0101 0011 0001.1010 BCD = 538.625 10

BCD到十进制或十进制到BCD的转换是一个相对简单的任务，但我们需要记住BCD数是十进制数而不是二进制数数字，即使它们是用比特表示的。十进制数的BCD表示很重要，因为大多数人使用的基于微处理器的系统需要在十进制系统中。

然而，虽然BCD易于编码和解码，但它不是存储数字的有效方式。在十进制数的标准8421 BCD编码中，表示给定十进制数所需的各个数据位的数量将始终大于等效二进制编码所需的位数。

例如，二进制从0到999的三位十进制数仅需要10位（ 1111100111 2 ），而在二进制编码的十进制中，相同的数字至少需要12 -bits（ 0011 1110 0111 BCD ）用于相同的表示。

此外，使用二进制编码的十进制数执行算术任务可能有点尴尬每个数字不能超过9.在BCD中添加两个十进制数字将产生一个可能的进位位1，需要将其添加到下一组4位。

如果二进制和添加的进位位等于或小于9（1001），相应的BCD数字是正确的。但是当二进制和大于9时，结果是无效的BCD数字。因此，最好将BCD数转换为纯二进制数，执行所需的加法，然后在显示结果之前将其转换回BCD。

然而，在微电子和计算机中使用BCD编码系统系统在二进制编码的十进制数据打算显示在一个或多个7段LED或LCD显示器上的情况下特别有用，并且有许多流行的集成电路可用于提供BCD输出或输出。

一个常见的IC是74LS90异步计数器/分频器，它包含独立的2分频和5分频计数器，可以一起使用以产生具有BCD输出的10分频计数器。另一个是74LS390，它是基本74LS90的双版本，也可以配置为产生BCD输出。

但最常用的BCD编码IC是74LS47和74LS48 BCD到7-段解码器/驱动器，它转换计数器的4位BCD码等，并将其转换为所需的显示代码，以驱动7段LED显示器的各个段。虽然两个IC功能相同，但74LS47具有用于驱动共阳极显示器的低电平有效输出，而74LS48具有用于驱动共阴极显示器的高电平有效输出。

二进制编码十进制解码器IC

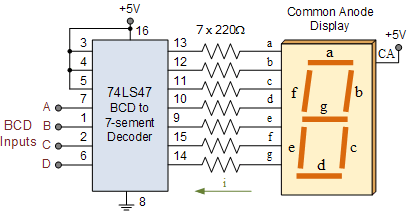
二进制编码的十进制摘要

我们在这里看到二进制编码的十进制或BCD只是十进制数字的4位二进制代码表示，每个十进制数字在整数和小数部分中替换为二进制等效。 BCD代码使用4位来表示0到9的10位十进制数字。

因此，例如，如果我们想要显示0到9（一位数）范围内的十进制数字，我们会需要4个数据位（半字节），0到99范围内的十进制数，（两位数）我们需要8位（一个字节），0到999范围内的十进制数，（三位数） ）我们需要12位，依此类推。使用单字节（8位）存储或显示两个BCD数字，允许字节保存00-99范围内的BCD编号，称为压缩BCD 。

标准二进制编码十进制代码通常称为加权8421 BCD代码，其中8,4,2和1表示从最高有效位（MSB）开始并向最低有效位开始的不同位的权重位（LSB）。 BCD码的各个位置的权重为： 2 3 = 8 ， 2 2 = 4 ， 2 1 = 2 ， 2 0 = 1 。

主要二进制编码十进制系统的优点在于，与纯二进制系统相比，它是一种快速有效的系统，可将十进制数转换为二进制数。但是BCD代码是浪费的，因为许多4位状态（10到16）没有使用，但十进制显示有重要的应用。

十进制数	BCD 8421代码
0	00000000
1	00000001
2	00000010
3	00000011
4	00000100
5	00000101
6	00000110
7	00000111
8	00001000
9	00001001
10（1 + 0）	00010000
11（1 + 1）	00010001
12（1 + 2）	00010010
...	...
20（2 + 0）	00100000
21（2 + 1）	00100001
22（2 + 2）	00100010
等，继续以四人为一组