

多款RLC电路分析说明
描述
串联RLC电路由交流电源串联的电阻,电容和电感组成
到目前为止,我们已经看到了三种基本无源元件:电阻,电感和电容在连接到正弦交流电源时具有非常不同的相位关系。
纯欧姆电阻器的电压波形与电流“同相”。在纯电感中,电压波形“导通”电流90° o ,给出表达式:ELI。在纯电容中,电压波形“滞后”电流90 o ,给出表达式:ICE。
这个相位差,Φ取决于电阻的无功值。正在使用的元件,希望现在我们知道,如果电路元件是电阻性的,电抗( X )为零,如果电路元件是电感元件则是正电阻,如果电容元件是电容元件则是负电阻,因此给出它们产生的阻抗:
元素阻抗
| 电路元素 | 阻力,(R) | Reactance,(X) | 阻抗,(Z) |
| 电阻 | <跨度> - [R | <跨度> 0 | <<<>>>> |
| 电感 | <跨度> 0 | <跨度>ωL | <<<>>>> |
| 电容器 | <跨度> 0 | <<<>>>> |
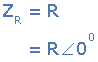 |
而不是分析eac h无源元件分开,我们可以将所有三个组合成一个串联的RLC电路。系列RLC电路的分析与双串联 R L 和 R C 的分析相同我们之前看过的子> 电路,除了这次我们需要考虑 X L 和 X C的幅度 找到整个电路的电抗。系列RLC电路被归类为二阶电路,因为它们包含两个储能元件,电感 L 和电容 C 。考虑下面的RLC电路。
系列RLC电路
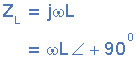
上面的RLC系列电路具有单个环路,流过环路的瞬时电流对于每个电路元件是相同的。由于电感和电容电抗的 X L 和 X C 是电源频率的函数,因此正弦响应因此,串联RLC电路的频率随频率而变化,ƒ。然后, R , L 和 C 元素的每个电路元件上的单个电压降将彼此“异相”为定义如下:
i (t) = I max sin(ωt)
纯电阻上的瞬时电压 V R 与电流“同相”
瞬时电压一个纯电感, V L “引导”电流90 o
纯电容器两端的瞬时电压, V C “滞后”电流90 o
因此, V L 和 V C 是180 o “异相”并相互对立。
对于上面的RLC系列电路,可以显示为:
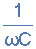
串联RLC电路中所有三个元件的源极电压幅度由三个中的三个组成单个分量电压, V R , V L 和 V C 目前所有三个组件共有。因此,矢量图将以当前矢量作为参考,三个电压矢量相对于该参考绘制,如下所示。
个别电压矢量
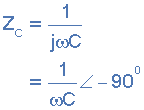
这意味着我们不能简单地将 V R , V L 和 V C 以查找电源电压所有三个分量中的 V S ,因为所有三个电压矢量指向关于电流矢量的不同方向。因此,我们必须找到电源电压, V S 作为向量组合在一起的三个分量电压的相量和。
Kirchhoff的环路和节点电路的电压定律(KVL)表明,在任何闭环周围,环路周围的电压降之和等于EMF的总和。然后将这个定律应用于这三个电压将为我们提供源电压的幅度, V S as。
系列RLC的瞬时电压电路
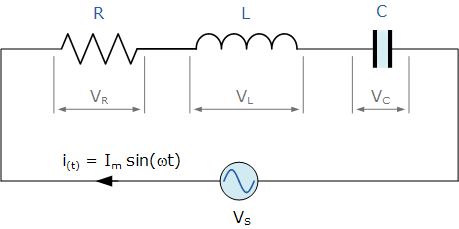
串联RLC电路的相量图是通过将上面三个单独的相量组合在一起并添加的这些电压矢量。由于流经电路的电流对于所有三个电路元件是公共的,我们可以将其用作参考矢量,其中三个电压矢量相对于它们以相应的角度绘制。
得到的矢量 V S 是通过将两个矢量相加得到的, V L 和 V C 然后将此总和添加到剩余的向量 V R 。在 V S 和 i 之间获得的最终角度将是电路相位角,如下所示。
相量图一系列RLC电路
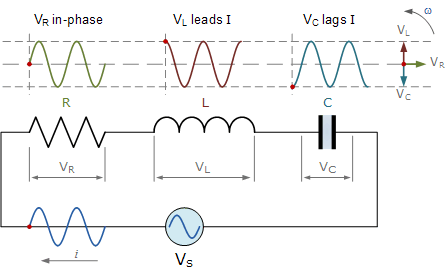
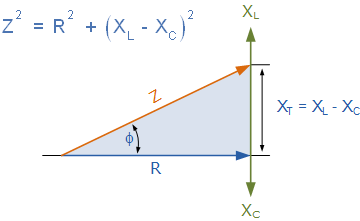
从上面右侧的相量图可以看出电压矢量产生一个矩形三角形,包括斜边 V S ,水平轴 V R 和垂直轴 V L -V C 希望你会注意到,这形成了我们最喜欢的电压三角,因此我们可以使用毕达哥拉斯的该电压三角形上的定理以数学方式获得 V S 的值,如图所示。
串联RLC电路的电压三角
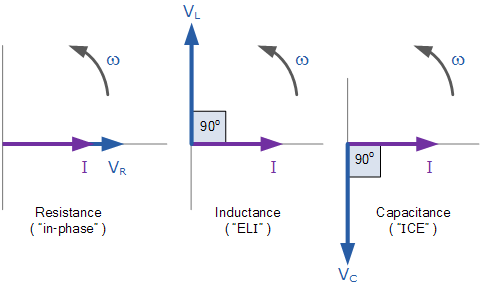
请注意,使用上述公式时,最终的无功电压必须始终为正值,即最小电压必须始终从最大电压中取出,我们不能为负值电压加到 V R 所以 V L -V C 是正确的>或 V <子> C -V <子>→ 。最大的最小值,否则 V S 的计算将是不正确的。
我们从上面知道电流具有相同的幅度和相位在一系列RLC电路的所有组件中。然后,每个元件两端的电压也可以根据流过的电流和每个元件的电压进行数学描述。
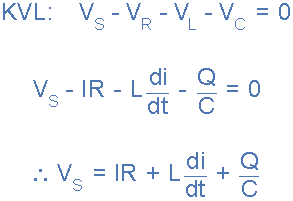
通过将这些值代入上面的毕达哥拉斯方程中的电压三角形将给出:
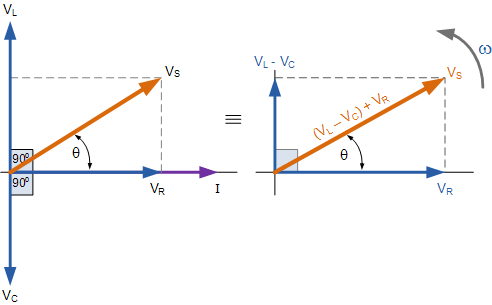
因此我们可以看到源电压的幅度与流过电路的电流幅度成正比。这个比例常数称为电路的阻抗,它最终取决于电阻以及电感和电容电抗。
然后在上面的RLC系列电路中,可以看出对电流的反对由三个部分组成, X L , X C 和 R 任何系列RLC电路的电抗 X T 定义为: X T = X → -X <子> C 或<跨度> X <子>Ť = X <子> C -X <子>→ 以较大者为准。因此,电路的总阻抗被认为是驱动电流通过它所需的电压源。
串联RLC电路的阻抗
当三个矢量电压输出时相互相位, X L , X C 和 R 必须与 R , X L 和 X 之间的关系相互“异相” C 是这三个组件的向量和。这将为我们提供RLC电路的总阻抗, Z 。这些电路阻抗可以用阻抗三角绘制和表示,如下所示。
串联RLC电路的阻抗三角
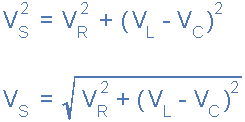
串联RLC电路的阻抗 Z 取决于角频率,ω和 X L 和 X C 如果容抗大于感抗, X C > X L 然后整个电路电抗是电容性的,给出一个超前相位角。
同样,如果感抗小于容性电抗, X L > X C 然后整个电路电抗是电感性的,给串联电路一个滞后的相位角。如果两个电抗是相同的并且 X L = X C 那么发生这种情况的角频率称为谐振频率并产生共振的影响我们将在另一篇教程中详细介绍。
然后,电流的大小取决于应用于串联RLC电路的频率。当阻抗 Z 达到最大值时,电流最小,同样,当 Z 达到最小值时,电流达到最大值。因此上面的阻抗公式可以重写为:
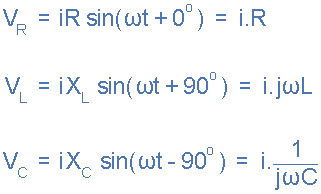
相角,θ 源电压 V S 和电流 i 与 Z <之间的角度相同阻抗三角形中的/ span>和 R 。取决于源电压是否超前或滞后电路电流,该相位角可以是正值或负值,并且可以从阻抗三角形的欧姆值数学计算为:
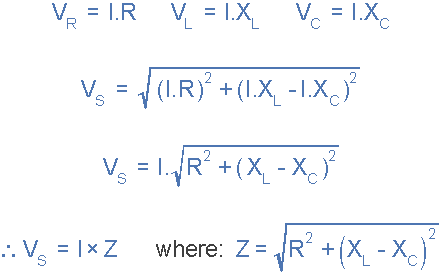
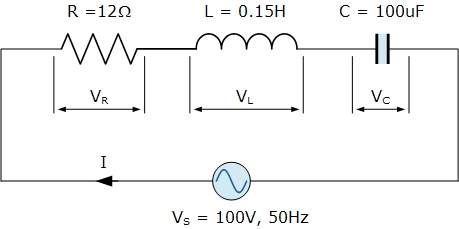
RLC系列电路示例No1
在100V,50Hz范围内串联一个RLC电路,其电阻为12Ω,电感为0.15H,电容为100uF供应。计算总电路阻抗,电路电流,功率因数并绘制电压相量图。
感应电抗, X L 。
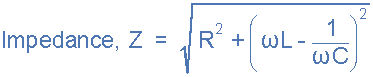
>
电容式电抗, X C 。
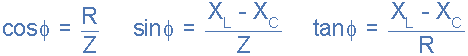
电路阻抗, Z 。
电路电流, I 。
 >
>
串联RLC电路的电压, V R , V L , V C 。
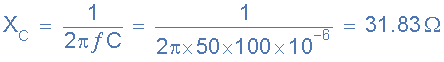
电路功率因数和相角,θ。
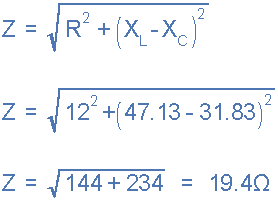
Phasor Diagram。
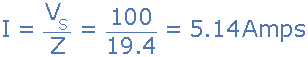
由于相位角θ计算为51.8 o 的正值,因此电路的总电抗必须是电感性的。由于我们已将电流矢量作为串联RLC电路中的参考矢量,因此电流“滞后”源电压51.8 o 因此我们可以说相位角是滞后的,如我们所证实的那样。助记符表达式“ELI”。
系列RLC电路摘要
系列RLC电路包含电阻,电感和电源电压 V S 是由三个分量组成的相量和, V R , V L 和 V C ,所有三个都是共同的。由于电流对所有三个元件都是通用的,因此在构造电压三角形时它被用作水平参考。
电路的阻抗是与电流的总阻抗。对于串联RLC电路,可以通过将电压三角形的每一边除以其电流 I 来绘制阻抗三角形。电阻元件两端的电压降等于 I * R ,两个电抗元件两端的电压 I * X = I * X L -I * X C ,而源电压等于 I * Z 。 V S 和 I 之间的角度为相角,θ。
当使用包含多个电阻的串联RLC电路时,电容或电感要么是纯的还是不纯的,它们可以全部加在一起形成单个元件。例如,所有阻力加在一起, R T =(R 1 + R 2 + R 3 ) ...等或所有电感的 L T =(L 1 + L 2 + L 3 ) ...等这样一个包含许多元素的电路可以很容易地减少到一个阻抗。
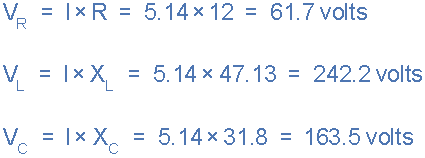
-
如何判断rlc串联电路达到谐振状态2024-03-09 6168
-
具体分析RLC谐振电路2023-06-08 30989
-
使用SPICE来进行简单RLC电路的时域分析的教程2022-11-30 1870
-
电源技术之RLC电路分析2022-05-11 4714
-
电源技术之RLC电路分析(一)2020-09-21 6774
-
如何使用SPICE软件进行RLC电路的时域分析2019-10-16 2369
-
RLC电路谐振特性的研究实验资料说明2018-12-11 2221
-
大规模RLC电路的计算机分析法_刘扬2017-03-19 991
-
电路设计--RLC串联电路2017-02-28 1156
-
RLC桥式整流滤波电路的频域分析及实验仿真2010-05-20 1060
-
应用拉普拉斯变换分析RLC电路2010-04-12 4885
-
RLC串联谐振电路的计算机仿真分析2010-03-30 1304
-
2003年第3期RLC电路特性分析程序2006-04-10 921
全部0条评论

快来发表一下你的评论吧 !

