三个布尔代数示例说明

布尔代数如何使用布尔代数定律减少数字门数的例子

布尔代数和布尔代数定律可用于识别数字逻辑设计中不必要的逻辑门减少功耗和成本所需的门数。

我们在本节中已经看到，数字逻辑功能可以定义并显示为布尔代数表达式或逻辑门真值表。所以这里有一些例子说明我们如何使用布尔代数来简化更大的数字逻辑电路。

布尔代数示例No1

构造一个真值表以下电路中 C ， D 和 Q 点的逻辑功能，并确定可用于替换整个电路的单个逻辑门。

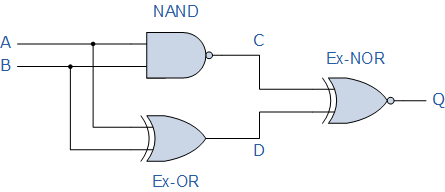
首先观察告诉我们该电路由2输入 NAND 门，2输入 EX-OR 门，最后输出端为2输入 EX-NOR 门。由于标记 A 和 B 的电路只有2个输入，因此输入只能有4种可能的组合（2 2 ）和它们是： 0-0 ， 0-1 ， 1-0 ，最后 1-1 。以表格形式绘制每个门的逻辑函数将为下面的整个逻辑电路提供以下真值表。

从上面的真值表中，列 C 表示由 NAND 门生成的输出函数，而列 D 表示输出函数来自 Ex-OR 门。这两个输出表达式都将成为输出端 Ex-NOR 门的输入条件。

从真值表中可以看出的输出当 A 或 B 中的任何一个输入处于逻辑 1 时，存在Q 。满足此条件的唯一真值表是 OR 门。因此，整个上述电路只能用一个2输入OR 门代替。

布尔代数示例No2

找到以下系统的布尔代数表达式。

系统由组成AND 门， NOR 门，最后是 OR 门。 AND 门的表达式为 A.B ， NOR 门的表达式为 A + B 。这两个表达式也是 OR 门的单独输入，定义为 A + B 。因此，最终输出表达式如下：

系统的输出为 Q =（AB） +（ A + B ），但符号 A + B 与De Morgan的符号 A 。 B 相同，然后替换 A 。 B 到输出表达式给出了 Q =（AB）+（ A 。 B ）的最终输出符号，这是 Exclusive-NOR 门的布尔表示法，如上一节所示。

输入	输出
A	B	C	D	Q
0	0	1	0	0
0	1	1	1	1
1	0	1	1	1
1	1	0	0	1

输入	中间体	输出
B	A	AB	A + B	Q
0	0	0	1	1
0	1	0	0	0
1	0	0	0	0
1	1	1	0	1

然后，上面的整个电路可以只用一个 Exclusive-NOR 门代替，实际上 Exclusive-NOR 门由这些单独的门组成函数。

布尔代数示例No3

查找以下系统的布尔代数表达式。

这个系统可能看起来比其他两个系统要复杂得多，但逻辑电路只包含简单的 AND ， OR 和 NOT 连接在一起的门。

与前面的布尔示例一样，我们可以通过依次写下每个逻辑门功能的布尔符号来简化电路为了给出 Q 输出的最终表达式。

当ALL门输入在逻辑电平“1”处为高电平时，3输入 AND 门的输出仅为逻辑“1”（ ABC ）。当一个或两个输入 B 或 C 处于逻辑电平“0”时，低 OR 门的输出仅为“1”。当输入 A 为“1”且输入 B 或时，2输入 AND 门的输出为“1” C 为“0”。当输入 ABC 等于“1”或 A 等于“1”并且两个输入时， Q 的输出仅为“1” B 或 C 等于“0”， A.（ B + C ）。

使用“de Morgan定理”输入 B 并输入 C 取消，以便在 Q 处产生输出，它们可以是逻辑“1”或逻辑“0”。然后，这只是输入 A 作为在 Q 输出所需的唯一输入，如下表所示。

输入	中间体	输出
C	B	A	ABC	B	C	B + C	A。（ B + C ）	Q
0	0	0	0	1	1	1	0	0
0	0	1	0	1	1	1	1	1
0	1	0	0	0	1	1	0	0
0	1	1	0	0	1	1	1	1
1	0	0	0	1	0	1	0	0
1	0	1	0	1	0	1	1	1
1	1	0	0	0	0	0	0	0
1	1	1	1	0	0	0	0	1

然后我们可以看到上面的整个逻辑电路只能被标记为“ A ”的单个输入所取代，从而将六个独立逻辑门的电路减少到只有一根电线，（或缓冲器） 。使用布尔代数的这种类型的电路分析可以非常强大并且可以快速识别数字逻辑设计中的任何不必要的逻辑门，从而减少所需的门数，电路的功耗以及成本