

基尔霍夫的电压定律及电路回路
描述
Kirchhoff的电压定律(KVL)是Kirchhoff的第二定律,它涉及闭路循环路径周围的能量守恒。
Gustav Kirchhoff的电压定律是第二定律他的基本定律我们可以用于电路分析。他的电压定律表明,对于闭环串联路径,电路中任何闭环周围的所有电压的代数和等于零。这是因为电路回路是闭合的导电路径,所以没有能量损失。
换句话说,环路周围所有电位差的代数和必须等于零:ΣV= 0 。请注意,术语“代数和”意味着要考虑环路周围的源极和电压降的极性和符号。
基尔霍夫的这个想法通常被称为能量守恒,当在闭环或电路周围移动时,您将最终返回到您在电路中开始的位置,因此返回到相同的初始电位,而环路周围没有电压损失。因此,环路周围的任何电压降必须等于沿途遇到的任何电压源。
因此,当将基尔霍夫电压定律应用于特定电路元件时,重要的是我们要特别注意代数符号,( + 和 - )电压在元素和电动势的电压下降,否则我们的计算可能是错误的。
但在我们看之前密切关注基尔霍夫电压定律(KVL),首先要了解单个元件(如电阻器)的电压降。
单电路元件
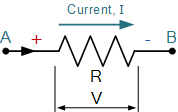
对于这个简单的例子,我们假设电流 I 与正电荷流方向相同,即传统电流。
这里,通过电阻器的电流从点 A 到 B ,即从正端子到负端子。因此,当我们沿着与电流相同的方向行进时,电阻元件上的电位会有下降,从而导致电压上的 -IR 电压降。 / p>
如果电流是从 B 点到 A 的相反方向,则会出现上升当我们从 - 电位移动到 + 电位时,电阻元件的电位会产生 + I * R 电压降。
因此,为了将Kirchhoff的电压定律正确地应用于电路,我们必须首先理解极性的方向,并且正如我们所看到的,电阻元件上的电压降的符号将取决于电流的方向。流过它。作为一般规则,当您沿着电动势源的方向移动时,您将在相同的电流方向上消耗电势并获得潜力。
闭合电路周围的电流方向可以是假设是顺时针或逆时针,可以选择任何一个。如果选择的方向与当前流的实际方向不同,结果仍然是正确有效的,但会导致代数答案有一个减号。
为了更好地理解这个想法,让看看单个电路回路,看Kirchhoff的电压律是否成立。
单回路循环
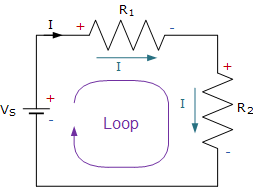
基尔霍夫电压定律表明,任何环路中电位差的代数和必须等于零,如:ΣV= 0。由于两个电阻 R 1 和 R 2 以串联方式连接在一起,它们都是一部分因此,相同的电流必须流经每个电阻器。
因此电阻上的电压降,R 1 = I * R 1 和电阻上的电压降,R 2 = I * R 2 由KVL给出:
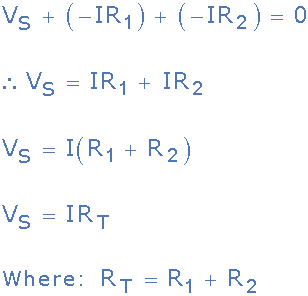
我们可以看到将Kirchhoff的电压定律应用于这个单闭环产生了串联电路中等效或总电阻的公式,我们可以对此进行扩展以找到电压降的值围绕循环。
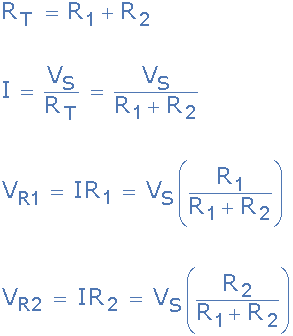
Kirchhoff的电压定律示例No1
三个电阻值:10欧姆,20欧姆和30欧姆分别串联连接12伏电池供电。计算:a)总电阻,b)电路电流,c)通过每个电阻的电流,d)每个电阻上的电压降,e)验证Kirchhoff的电压定律,KVL是否成立。
a)总阻力(R T )
R T = R 1 + R 2 + R 3 =10Ω+20Ω+30Ω=60Ω
然后总电路电阻R T 等于60Ω
b)电路电流(I)
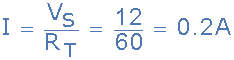
因此总电路电流I等于0.2安培或200mA
c)通过每个电阻的电流
电阻串联在一起,它们都是同一回路的一部分,因此每个都经历相同的电流。因此:
<跨度> I <子> R1 = I R2 = I R3 = I SERIES = 0.2安培
d)每个电阻上的电压降
V R1 = IxR 1 = 0.2x10 = 2伏
V R2 = IxR 2 = 0.2x20 = 4伏
V R3 = IxR 3 = 0.2x30 = 6伏
e)验证Kirchhoff的电压定律
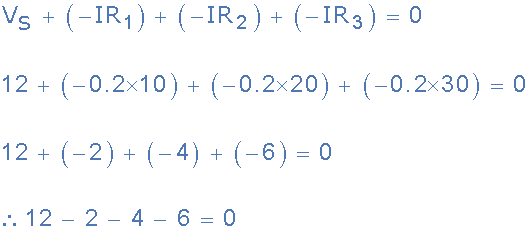
因此,基尔霍夫的电压定律适用于闭环周围的单个电压下降加起来。
基尔霍夫的电路回路
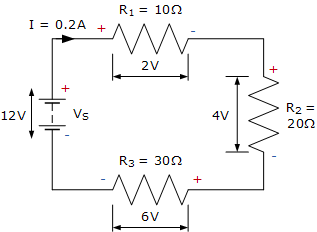
我们在这里看到基尔霍夫的电压定律,KVL是基尔霍夫的第二定律和状态所有电压的代数和下降,当你从一个固定点绕回一个闭合电路并返回到同一点,并考虑极性时,总是为零。那就是ΣV= 0
基尔霍夫第二定律背后的理论也被称为电压守恒定律,这对于我们处理串联电路特别有用,串联电路也可作为分压器,分压电路是许多串联电路的重要应用。
-
什么是基尔霍夫电压定律 什么是基尔霍夫电流定律2024-02-18 12429
-
基尔霍夫定律体现了什么守恒2024-01-10 2623
-
基尔霍夫定律适用于什么电路?2023-11-24 16367
-
什么是基尔霍夫电压定律2021-09-30 2994
-
基尔霍夫的电压定律和能量守恒分析2020-10-27 3501
-
基尔霍夫电路法分析2020-10-05 3574
-
基尔霍夫电流定律例题详解_基尔霍夫电压定律例题详解2017-08-15 257019
-
请问基尔霍夫定律的问题2017-05-17 4922
-
基尔霍夫定律及其应用2009-09-24 4841
-
基尔霍夫定律2009-07-27 12065
-
基尔霍夫定律与叠加原理2008-11-02 18813
-
基尔霍夫定律实验2008-09-24 39973
全部0条评论

快来发表一下你的评论吧 !

