星三角如何转型？

Star-Delta转换和Delta-Star转换允许我们将三相配置中连接在一起的阻抗从一种类型的连接转换为另一种类型

我们现在可以解决简单的并联系列或者桥式电阻网络使用基尔霍夫电路定律，网格电流分析或节点电压分析技术，但在平衡的三相电路中，我们可以使用不同的数学技术来简化电路分析，从而减少所涉及的数学量本身是一件好事。

标准三相电路或网络采用两种主要形式，其名称代表电阻的连接方式，Star连接网络它具有字母符号， Y （Y形）和Delta连接网络，其符号为三角形，Δ（delta） 。

如果在一种配置中连接3相，3线电源或甚至3相负载，它可以是ea通过使用星形三角洲转换或Delta Star转换过程，将其转换或改变为另一种类型的等效配置。

电阻网络由三个阻抗组成可以连接在一起形成 T 或“Tee”配置，但也可以重新绘制网络以形成星或Υ键入网络如下所示。

T型连接和等效星形网络

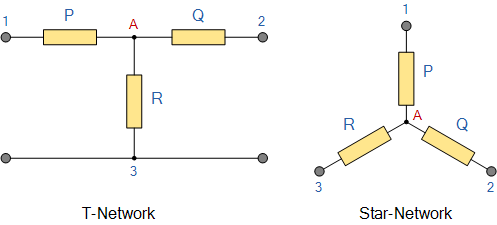
正如我们已经看到的，我们可以重新绘制上面的 T 电阻网络，以生成电气等效的Star或 Y 型网络。但我们也可以将 Pi 或π型电阻网络转换为电等效Delta或Δ型网络。如下所示。

Pi连接和等效Delta网络

现已确切定义什么是星和Delta连接的网络，可以将 Y 转换为等效的Δ电路，还可以使用转换过程将Δ转换为等效的 Y 电路。

此过程允许我们在各种电阻之间产生数学关系我们一个星三角变换以及Delta Star变换。

这些电路变换允许我们改变三个连接的电阻（或阻抗）对于星形或三角形连接电路，在端子 1-2,1-3 或 2-3 之间测量它们的等效值。然而，由此产生的网络仅相当于星形或三角形网络外部的电压和电流，因为内部电压和电流不同，但每个网络将消耗相同的功率并且彼此具有相同的功率因数。

Delta Star Transformation

要将delta网络转换为等效的星形网络，我们需要推导出一个转换公式，用于在各个终端之间将各种电阻相互等同。考虑下面的电路。

Delta到Star Network

比较终端之间的电阻 1 和 2 。

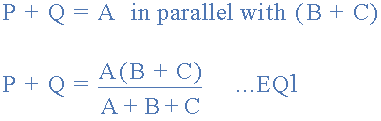
终端之间的电阻 2 和 3 。

终端 1 和之间的电阻3 。

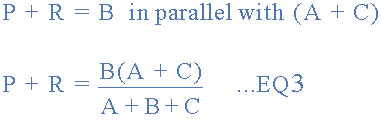
现在给出了三个方程式，并从等式2中得出方程式3：

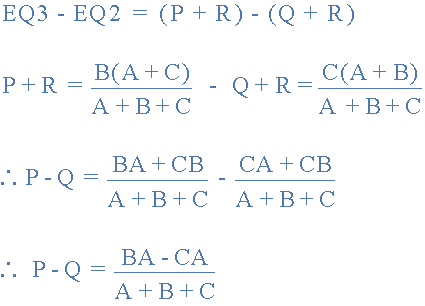
然后，重写等式1将给我们：

加在一起等式1和等式3的结果减去等式2给出：

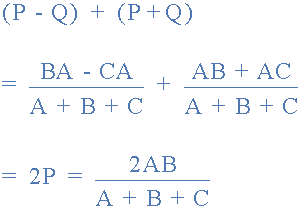
从中给出了电阻 P 的最终等式：

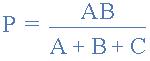
然后总结一下上面的数学，我们现在可以说星形网络中的电阻 P 可以找到等式1加（等式3减去等式2）或 Eq1 +（ Eq3 - Eq2）。

类似地，为了在星形网络中找到电阻 Q ，等式2加上等式1的结果减去等式3或 Eq2 +（Eq1 - Eq3）这使我们将 Q 转换为：

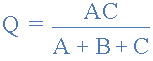
再次，在星形网络中找到电阻 R ，等式3加上等式2减去等式1或 Eq3 +（Eq2 - Eq1）的结果，这给了我们 R 的转换为：

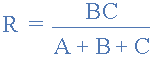
将三角洲网络转换为星形网络时，所有的分母都是转换公式是相同的： A + B + C ，它是所有delta电阻的总和。然后，为了将任何三角洲连接的网络转换为等效的星形网络，我们可以将上述转换方程概括为：

Delta to Star Transformations Equations

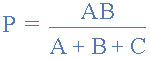
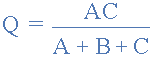
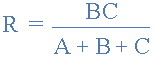
如果三角网络中的三个电阻器的值都相等，则等效星形网络中的合成电阻器将等于三角形电阻值的三分之一。这为星形网络中的每个电阻分支提供了以下值： R STAR = 1/3 * R DELTA ，这与说： （R DELTA ）/ 3

Delta - Star示例No1

将以下Delta电阻网络转换为等效的星形网络。

Star Delta转换

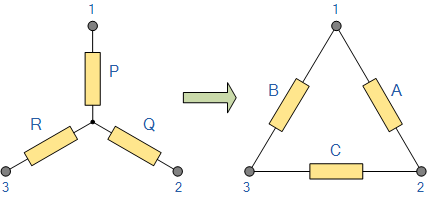
Star Delta转换与上述相反。我们已经看到，当从三角网络转换到等效星形网络时，连接到一个端子的电阻器是连接到同一端子的两个三角形电阻的乘积，例如电阻器 P 是产品连接到端子1的电阻器 A 和 B 。

通过重写先前的公式，我们还可以找到转换电阻星的转换公式网络到等效的三角洲网络，为我们提供了一种产生星形三角形变换的方法，如下所示。

星形到三角形的转换

三角形任何一侧的电阻值Δ网络是星形网络中所有双电阻组合的总和除以“直接相对的星形电阻” “找到了三角形电阻器。例如，电阻 A 的格式为：

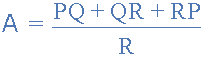
关于端子3和电阻 B 给出：

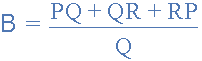
关于端子2，电阻 C 给定为：

关于终端1。

通过将每个等式除以分母的值，我们最终得到三个单独的转换可用于将任何三角形电阻网络转换为等效星形网络的公式，如下所示。

星三角形变换方程

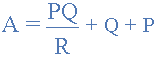
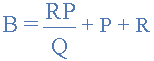
关于将星形电阻网络转换为等效三角网络的最后一点。如果星形网络中的所有电阻器的值都相等，则等效三角形网络中的合成电阻器将是星形电阻器的三倍，并且相等，给出： R DELTA = 3 * R STAR

Star - Delta示例No2

将以下Star Resistive Network转换为等效的Delta网络。

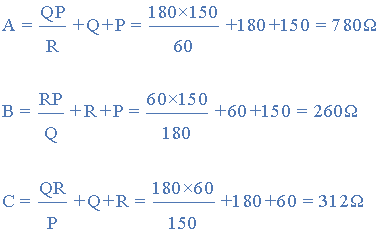
星际转型和Delta Star Transformation允许我们将一种类型的电路连接转换为另一种类型，以便我们轻松分析电路。这些变换技术可用于对包含电阻或阻抗的星形或三角形电路产生良好效果。