

电压电流采集技术——数据采集和电量参数计算
描述
电机作为一种重要的驱动设备,尤其三相电机,在日常生活以及工业之中有着极为广泛的运用,引起了越来越多的人的关注和重视。然而基于三相电机本身具有的特点,其使用环境复杂多样,在这样的情况下,使得在运转过程中,常常出现各种意想不到的问题,给正常的生产经营带来诸多的问题和困难,对设备的性能造成了不可逆的破坏,同时还极可能造成各种危险和事故。面对这样的情况,电机的故障诊断技术和方法得到了迅速发展。
目前,电机故障诊断的方法较多,如神经网络、专家学习、深度学习等。但基于电压电流的诊断是工程实施最方便的方法,而用于电机故障诊断的电压电流数据是需要电流电压的波形数据,这必然就涉及到电流电压的采集以及数据分析。
本文主要介绍电流电压数据采集和电量计算方面的主要技术方法。
电压电流波形采集
工业现场中的电流电压信号是模拟量数据,都是随时间连续变化的,称为连续信号。但对于计算机来说,处理这些连续的信号显然是无能为力,要使计算机能够识别、计算、处理这些连续信号就必须将其转化为离散信号,将连续信号转换为离散信号的过程就叫采样。因此,要分析电流电压的数据,需要模拟量的电流电压数据进行性采样。在模拟量采集领域,必然遵循采样定理,而最重要也是基本的采样定理便是香农采样定理。
1香农采样定理
香农采样定理,又称内奎斯特采样定理,是美国物理学家内奎斯特于1924年提出的一个理论。该理论是信息论,特别是通讯与信号处理学科中的一个重要的基本结论。
香农采样定理定义:
为了不失真地恢复模拟信号,采样频率应该不小于模拟频谱中最高频率的2倍,即:
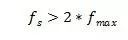
我们可以同构不同速率测量的正弦波来理解其原因
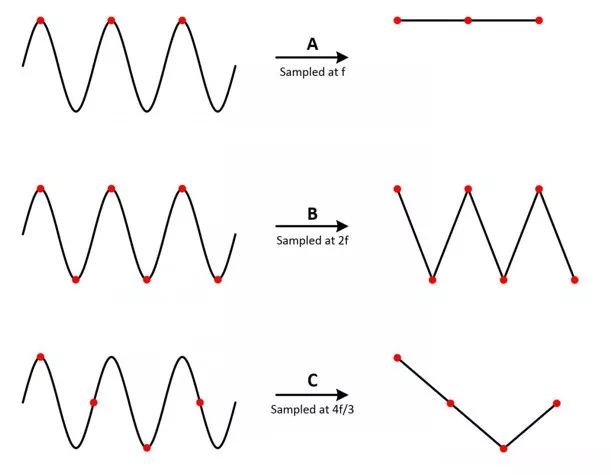
图1采样率过低的波形重构图
情况A,频率f的正弦波以同一频率采样,这些采样标记在原始信号的左侧,在右侧构建时,信号错误地显示为恒定直流电压。
情况B,采样率是信号频率的两倍。现在信号显示为三角波。这种情况下,f等于奈奎斯特频率,这也是特定采样频率下为了避免混叠而允许的最高频率分量。
情况C,采样率是4f/3。此时重构的波形无法准确的还原原波形信号。
可见,采样率过低会造成波形重构不准确。因此,为了无失真地恢复原波形信号,采样率fs必须大于被测信号感兴趣最高频率分量的两倍。通常希望采样率大于信号频率约五倍。
2UIM采样电路
公司研发的电压电流采集终端UIM实现了电机运行时电流电压数据的采集、转换和分析,具有采集精度高,传输数据量大,支持信号类型多,运行稳定等优点。目前已在造纸行业、煤机行业、电机制造业、水泥行业等场合得到了应用。
电压电流采集终端使用了模拟转换芯片ADS1258进行模拟信号的采集和转换。
电量参数计算
电机电量参数包含功率因数、有功功率、无功功率、电压RMS、电流RMS、电压不平衡、电流不平衡、负载率、频率、总谐波率等。
电量参数均是由电流电压的波形数据计算而来。其中电压RMS可根据实时监测的电压波形数据进行线电压和相电压的转换以及积分求得,同理电流RMS也可以用同样的方法得到;电压不平衡度、电流不平衡度、负载率、总谐波率的计算也比较简单;而有功功率和频率的计算稍微复杂,下面主要介绍有功功率和频率的计算方法。
1有功功率测量方法
在三相电路的功率测量中,主要测量方法有二瓦计法和三瓦记法两种方法。
二瓦计法的理论依据是基尔霍夫电流定律,适用于在三相回路中只有三个电流存在的场合,如:a、三相三线制接法,中线不引出(只能采用二瓦计法);b、三相三线制,中线引出但不与地线或实验电源相连的场合。
三瓦计法由于需要采用中性点作为电压的参考点,因此该方法适用的场合如:a、三相三线制,中性线引出,但中性线不与电源或地线连接的场合;b、三相四线制,由于无法判断三相负载是否平衡或是否中性线上有零序电流产生,只能采用三瓦计法。
可见,对于不同的接线方式场合,应选择合适的功率测量方式,才能得到准确的功率参数。目前,已经部署UIM的工业现场采用的电压互感器为三相三线制,并且没有引出中性线,从电压传感器出来的信号是表示三相电机的线电压,从电流互感器出来的信号是表示电机的三相电流信号。因此,采用的功率测量方法是二瓦计法。
二瓦计法的理论依据是基尔霍夫电流定律:在集总电路中,任何时刻,对任意节点,所有流入流出节点的之旅电流的代数和恒等于零。
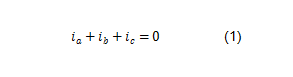
假设三相负载的中线为N,依据电压的定义:
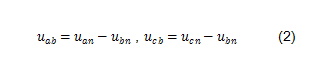
三相瞬时功率:
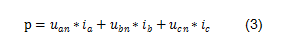
将式(1)和式(2)代入式(3),得
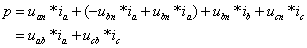
因此,有功功率等于瞬时功率在一个周期内求积分再求平均,得到:
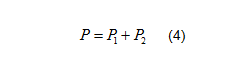
P为三相电路有功功率的总和,为在一个周期内的积分的平均值,为在一个周期内的平均值。在正弦稳态电路中:
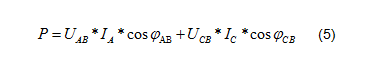
即: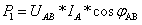
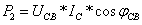 式中,
式中,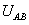
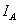
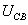
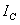 均为正弦电压电流的有效值;
均为正弦电压电流的有效值;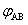 为
为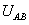 和
和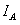 的相位差。
的相位差。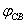 为
为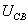 和
和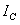 的相位差。
的相位差。
从变换的公式中可以看出,采用这种方法进行三相总功率测量时,只需要测量两个电压和两个电流,这就是二瓦计法的推导原理及由来。
2频率计算——FFT
工频50Hz下的电压电流波形中包含有若干频率的杂波,根据波形数据计算出电压电流的频率,目前常用的是快速傅里叶变换(FFT)。
快速傅里叶变换(fastFouriertransform)是1965年由J.W.库利和T.W.图基提出的,是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的,简称FFT。
FFT的基本思想是把原始的N点序列,依次分解成一系列的短序列。充分利用DFT计算式中指数因子所具有的对称性质和周期性质,进而求出这些短序列相应的DFT并进行适当组合,达到删除重复计算,减少乘法运算和简化结构的目的。特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。下面对FFT和DFT的计算量进行了简要对比分析。
有限长离散信号x(n),n=0,1,…,N-1的DFT定义为:
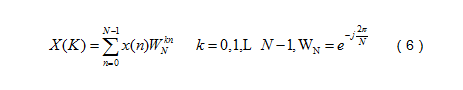
可以看出,DFT需要计算大约N2次乘法和N2次加法。当N较大时,这个计算量是很大的。利用WN的对称性和周期性,将N点DFT分解为两个N/2点的DFT,这样两个N/2点DFT总的计算量只是原来的一半,即(N/2)2+(N/2)2=N2/2,这样可以继续分解下去,将N/2再分解为N/4点DFT等。对于N=2m点的DFT都可以分解为2点的DFT,这样其计算量可以减少为(N/2)log2N次乘法和Nlog2N次加法。
下面简要介绍FFT的基本思路:

其中X1(k)和X2(k)分别为x1(n)和x2(n)的N/2点DFT。由于X1(k)和X2(k)均以N/2为周期,且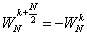 ,所以X(k)又可表示为:
,所以X(k)又可表示为:
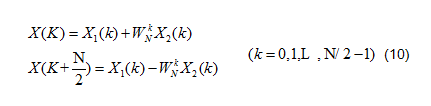
上式的运算可以用图2表示,根据其形状称之为蝶形运算。依此类推,经过m-1次分解,最后将N点DFT分解为N/2个两点DFT。
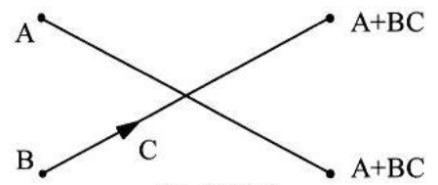
图2FFT的蝶行运算
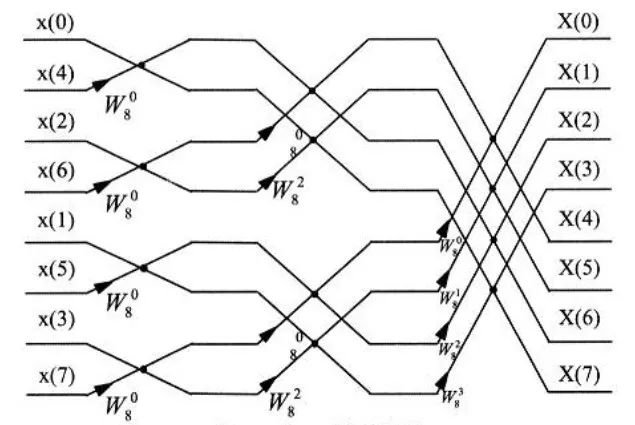
图38点FFT分解流程图
结束语
上面简单讲述了进行电压电流数据采集时使用到的原理,以及进行电量参数计算所用到的计算方法的基本思想,希望通过上述的阅读,能够对数据采集和电量参数计算有所基本了解,以便更好地交流或学习。
-
labview数据采集图解2008-08-03 42147
-
CRIO数据采集2014-04-14 4776
-
怎么用u***-204数据采集卡采集电压电流信号,并同步显示2014-10-20 3319
-
什么是数据采集?2016-01-28 4722
-
新手求教:NI数据采集卡如何采集压力传感器的电流信号?2017-04-14 20634
-
数据采集卡入门2019-01-10 7154
-
数据采集卡如何运用2019-01-17 4925
-
数据采集系统具有的功能是什么2021-09-10 2275
-
ADC基于stm32的电压电流采集2022-03-22 8112
-
数据采集方法有哪些2018-03-07 54414
-
如何使用STM32单片机实现数据采集系统2020-09-24 4155
-
数据采集模块的工作原理是什么2021-08-02 11416
-
物通博联数据采集网关支持电流电压模拟量数字量485数据采集2024-02-02 834
-
电力数据采集网关是什么2024-06-28 1618
-
plc边缘计算数据采集网关是什么2024-08-07 1051
全部0条评论

快来发表一下你的评论吧 !

