

数字电路知识之数制也称计数制
模拟技术
描述
数制,提起数制,也许我们不会有太多的感觉。我们习惯了十进制。也就是最平常的数字。但是我们在大一学习过C语言,或者C++,又了解了二进制,八进制,十六进制。
相信很多人当时就感觉,这些进制咋那么奇怪呢。现在,让我尝试着,解答一下这种奇怪。首先,以十进制为例。
(1) 计数符号: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
计数符号呢,我们在纸上写一下,然后呢,看着这些数字,或者说符号,他们都是一种表达数字的方式。在十以内,每个数字表示其本来的含义,也就是,1表示1,2表示2,我们的名字表示我们自己。当我们要表示一个大于十进制数的时候,计数符号会加入很多奇怪的东西。
比如十六进制加了A,B,C,D,E,F,这六个字母,看起来和数字毫无关系,但是呢,我们给它定义一下,A就是10,B就是11,C就是12,D就是13,E就是14,F就是15。看起来可能很迷糊,我看着也迷糊,咱先写下来。
A->10,B->11 甚至可以当成映射,函数。比如说,F(x),x可以取0-9,A-F。然后F(x)的值为0-15。选择一个自己的记忆方法,如果有其他方法也可以分享。
现在计数符号总结一下,就是个计数符号,表示数字的。数字啊,0-9表示0-9。其他的字母呢,或者其他的符号,规定这个字母啊还是符号啊是什么值。
(2) 进位规则: 逢十进一
这个很简单记忆,几进制,就逢几进一。这个好像没啥能说的,记一下吧。
(3) 十进制数按权展开式
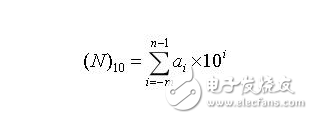
这个要说明。这个十进制数的高位后边的0个数+1,就是n。比如,我们看1000.00,他的高位就是千,也就是4。然后这n-1就是3。这个最低位呢,看的是小数位。这个小数位是百分位,这个m呢就是2。也可以数前边的0来判断m。
例: 1234.56=1×10^3 +2×10^2 + 3×10^1 + 4×10^0+5×10^-1 +6×10^-2,这个^表示次方的意思。
-
什么是进位计数制 PLC常用数制及转换方法介绍2023-08-20 1812
-
什么是进位计数制?为什么要进行数制间的转换?PLC数制转换方法2023-08-12 11742
-
PLC中常用数制及各进制的转换方法总结2022-10-24 6784
-
单片机中数制与数制的转换是怎样实现的2022-04-12 2981
-
进位计数制系统是什么?如何表示?2021-12-23 1058
-
干货 | PLC中常用数制及如何转换2019-06-24 5727
-
PLC常用数制及转换方法2019-05-06 3822
-
探析PLC常用数制及转换方法2019-01-21 3455
-
深度分析PLC常用数制及转换方法2019-01-18 3674
-
数字电路教程课件之数制和码制的详细资料说明2018-12-28 1255
-
浅析PLC常用的数制及其转换方式2018-10-31 3366
-
PLC常用数制的解析及相互转换的方法2017-12-25 5780
-
进位计数制及其转换方法过程详解2017-11-30 36911
-
数字电子电路技术--数制与码制2017-05-01 2335
全部0条评论

快来发表一下你的评论吧 !

