如何对系统建立数学模型

本次主要想写一下关于单相光伏并网逆变器的环路控制问题，即如何对系统建立数学模型， 以及选定环路调节器的参数（主要是逆变器电流环），如何减小并网电流的 THD。通常光伏逆变器的控制都是数字控制，所以本贴最后还会讲如何将选定的控制器参数转化为数字控制代码中的参数。

概述

单相光伏并网逆变器的拓扑结构通常为两级电路，前级 boost 升压电路＋后级的逆变并网 电路，这两级电路通常需要 4 个控制环，前级：boost 的电流内环（控制 boost 电感电流）+boost 电压外环（控制光伏电池板电压）；后级：inverter 电流环（控制逆变器电感电流）+bus 电压 环（中间母线电压）。电路结构如下：

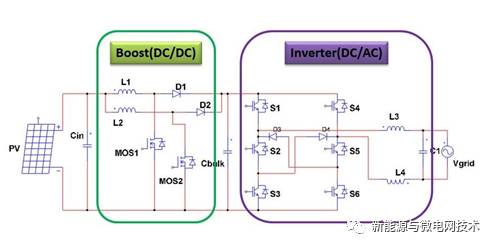
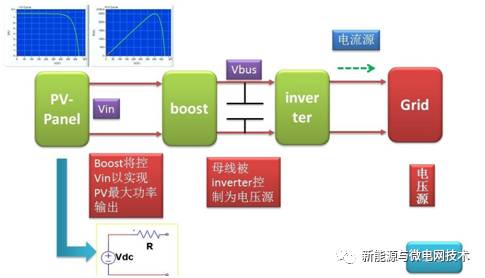
让我们对电路的各端口的源特性进行分析一下，因为并网逆变器输出端接的是电网，是一 个强电压源，所以逆变器的输出必须是一个电流源特性，因为地球人都知道，两个电压源不可 以并联。如下图：电池板的输出既不是一个电压源也不是一个电流源，而是相当于一个电压源 与一个电阻串联的端口特性，通过控制 boost 的输入电压（即电池板输出电压）可以使电池板 输出不同的功率；中间母线被一堆大电容搞成一个相对来说稳定的电压源，把电路的前后两级 从控制的级别解耦开；inverter 的输出需要被控制成一个电流源；

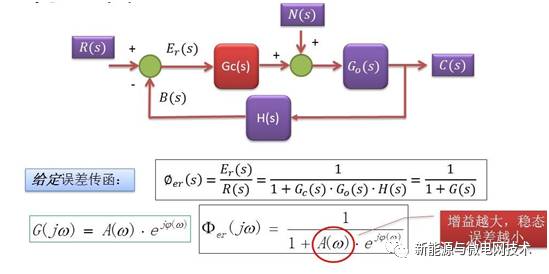
说到控制，直白的说就是让目标控制量尽可能的跟踪给定量，那么控制的稳态误差为 0（目 标量与给定量）的条件是啥：当然大家都知道：控制系统实现对某一频率信号控制的稳态误差 为 0 的条件是——系统开环 bode 图（或者控制器的 bode 图）在此频率点具有无限大增益。

上一张图给大家说明：将一个闭环系统的输入输出传递函数写出来后，可以得出，某个频 率点对应的增益越大，稳态误差越小。

前级 boost 电路的控制，无论内环还是外环，都是控制的直流量，并且控制目标为外环的 电压（即 PV 板的电压）。所以 boost 级的控制参数设计仅以开环 bode 图能够实现高增益（系 统稳定的前提下）为目标即可。因为有朋友问过我为什么前级 boost 要用双环，所以这里插入 一段解释一下：

实际上前级 boost 用双环有 3 个作用：

1）电流限幅。当光伏曲线为低电压大电流的时候，可以对电流环给定进行限幅以保证系 统安全工作在一个非最大功率点的位置。

第一点很好理解，对外环的输出（即内环的给定）限幅，就可以对电流进行限幅，保证其 不会超过额定电流稳定工作。

2）防止电感电流变化太快而造成器件损坏或者电感饱和。

3）电压环降阶，电压环由二阶振荡系统变为一阶系统。第 2 条和第 3 条可以一起解释。

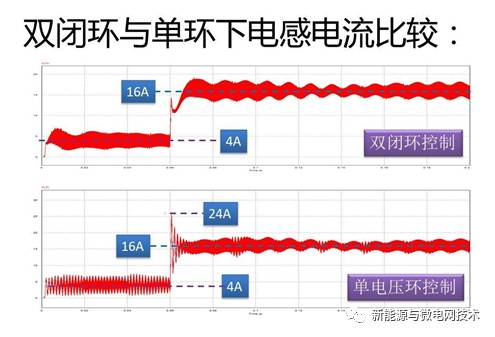
先来看一下单环和双环的仿真结果对比：下图中，在输入功率突然增加的时候，同样是从4A 突变到 16A，双闭环系统的电流振荡明显好很多，因此第 2 条就很好解释。

那么为什么会出先这个情况，就是第三条。单环系统的传递函数是一个二阶振荡环节，而 双闭环系统则是一个一阶系统。

我们从传递函数和 bode 图来看：

第一图是从占空比到电压的传递函数及 bode 图，即只有一个单电压环时候，其传递函数 有一对共轭极点，所以有一个振荡点。用 PI 调节器去控制，这个振荡怎么都会存在，表现在 波形上就是上图的情况。（bode 图中实线为幅频特性，坐标轴为左边；虚线为相频特性，坐 标轴为右边，下同。）

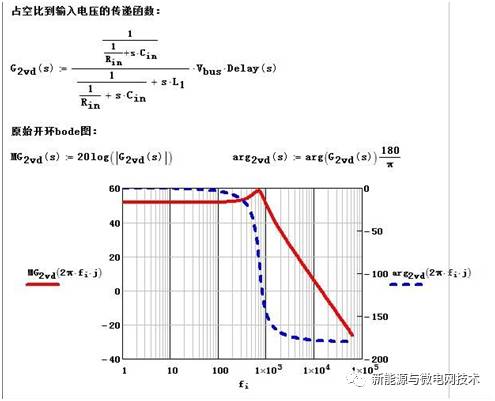
而加入电流内环以后，电流内环调好之后，整个电流内环的闭环会化解为一个比例环节（在 电流环带宽范围内），电压环就会降阶为一个一阶系统，不会存在振荡现象了。

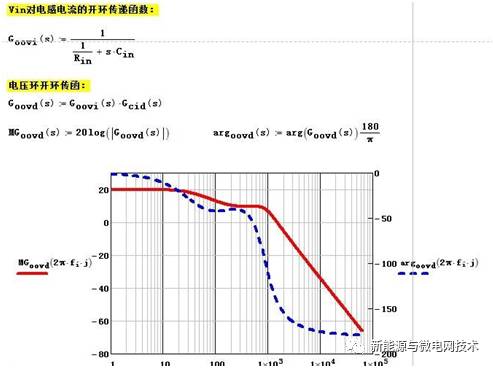
inverter 的环路控制

我们主要讨论后级 inverter 的控制，inverter 的电感电流为被控电流，间接的也是并网电 流的控制量（LC 滤波器情况，LCL 滤波器不在这里讨论），因此 inverter 电流内环的电流波形 质量的控制非常关键。

对了，我们之所以可以把前后级的控制分开讨论，是因为中间母线大电容在开关小信号级 上是相当于短路的，也就是前后级被母线大电容解耦。

inverter 电流环控制

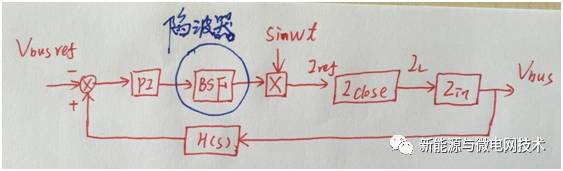
我们先给出 inverter 级的电路模型以及控制框图：

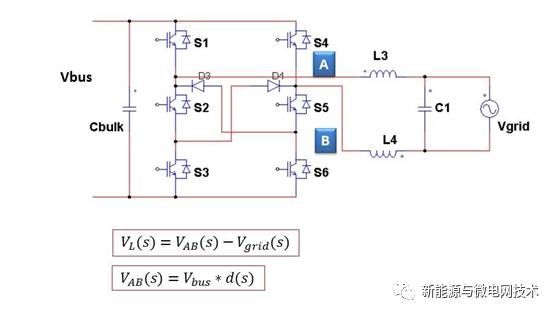
根据电路推演，可以得出电流内环以及 Vbus 电压外环的双环控制框图：

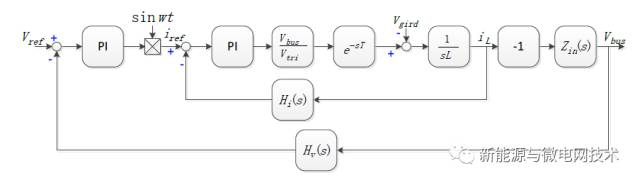
逆变器可以看做一个稳态工作点在变化的 buck 电路，所以建立小信号模型时候类似于 buck 电路，建模过程呢，简单说一下，首先将电网 Vg 看做一个扰动量，在建模时候不加考虑。先对储能元件（通常是电感和电容）列出微分方程，然后对微分方程中的变量（随着开关闭合 会变化的量）加入小信号扰动，然后化解方程，将不含微分因子项和微分因子乘积的项均去掉， 然后对剩下的部分做拉氏变换，就会得到小信号模型，将两个小信号模型方程（电容一个，电感一个）化解就会得到占空比到电感电流的传函或者占空比到电容电压的传函。那么单相并网 逆变器的占空比到电感电流的传函如下：

看起来很简单是不是，呵呵！

其 bode 图如下：相角为-180 度时候，幅值仍然大于 0 分贝，因此系统不稳定；系统起始 相角为-90，如果使用純积分控制，则起始相角会变成-180，且没有响应的零点来拉回相角， 因此电流环调节器必须是带有一个零点、一个积分（起始幅值斜率为-40db/dec，可以提高低 频部分的增益，减小低频部分稳态误差）的环节，那么 PI 调节器就是这样的控制器。

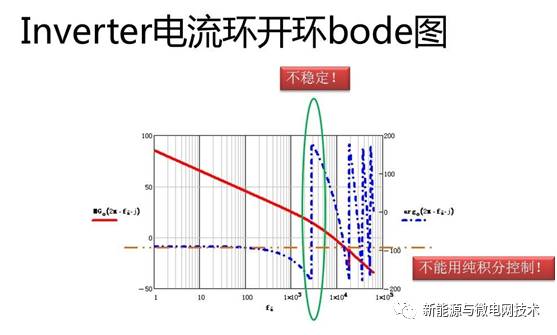
加入 PI 调节器后的开环 bode 图：在 mathcad 中动态调整 Kp、Ki 的值，保证在低频增 益足够高（穿越频率足够大）的情况下，使幅值穿越 0 分贝线时候相角值大于-180 度大约 20db 以上。这样系统即稳定又稳态误差又小。

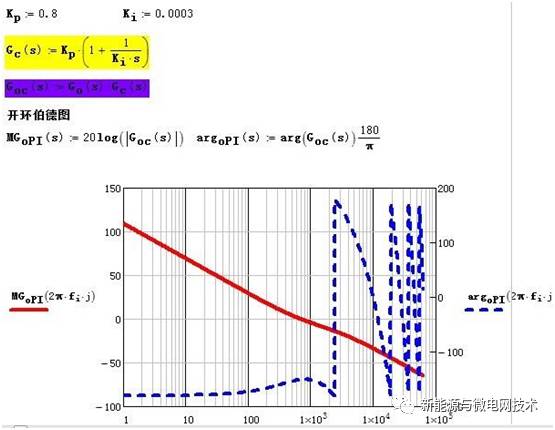
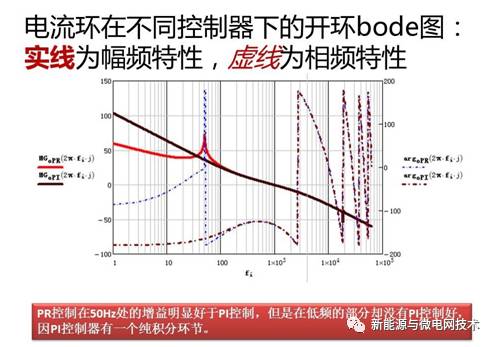
大家平时肯定也有经验，就是对交流信号控制的时候，总是不能完全跟踪，即输出与给定 是由静差的。这一点可以从 bode 图上看出来，在 50Hz 处，可以看到其增益是一个有限值， 根据我们前面所说，对某一频率信号实现无静差控制的条件是其开环增益在此频率点的增益为 无限大，比如一个带积分环节的传递函数，在 0HZ（即直流）处的增益就是无限大的。因此 PI 调节器可以对直流信号实现无静差控制。那么交流信号，通常频率为 50Hz，在此处的开环 增益往往不是无限大，因此通常调节器对交流信号往往是有差控制，这也是输出并网电流 THD 形成的一个原因。

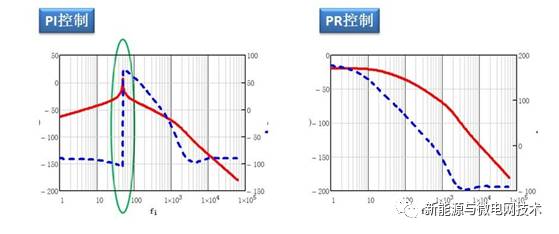
为了解决在 50Hz 处增益的问题，现在很多人使用比例谐振调节器（PR），这个调节器在 谐振频率处可以使增益达到一个比较高的点。我先放上传递函数和 bode 图：

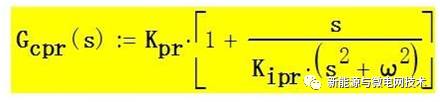
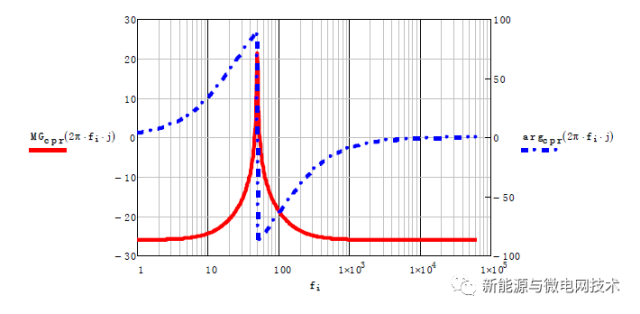
从 PR 调节器的 bode 图中可以可以看出，与 PI 调节器在频率越低出增益越大（直流处理 论增益无穷大）不同，PR 调节器幅频特性在 50Hz（谐振频率）处的增益很大，因为可以特 别改善 50Hz 频率的波形控制。

当然无图无真相，无实验无说服力，下面 PO 仿真波形 VS 实验波形：

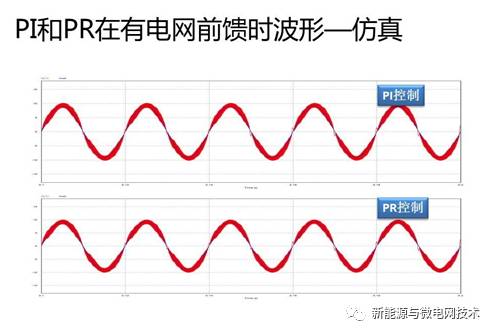
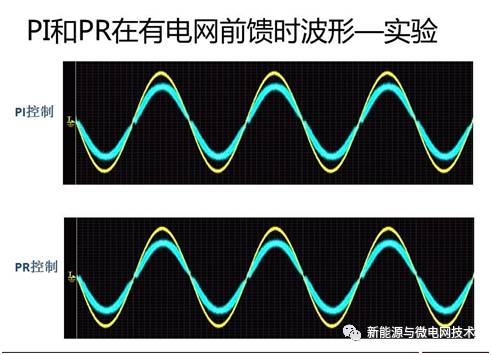
当然我们肉眼凡胎，看不出差别，下面上 THD 分析：其中 Ithd1 为对电流波形的 THD 测 量：结果显而易见

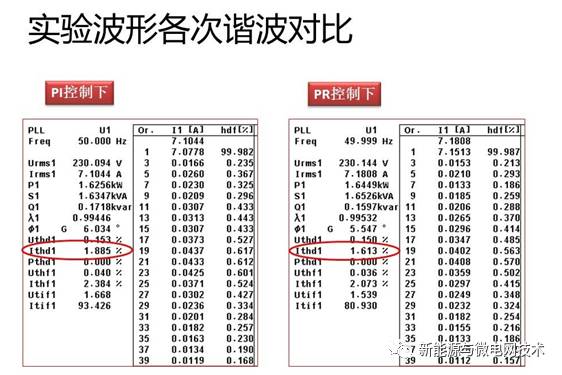
当然，有的同学说这不行，你得弄点让我们从波形上能看出来的东东证明，那好吧。我们看看在小功率的时候控制情况对比：（白底图为仿真对比，黑图为实验对比）

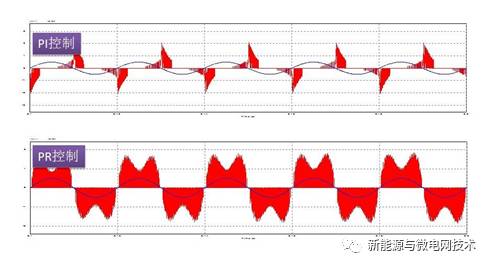
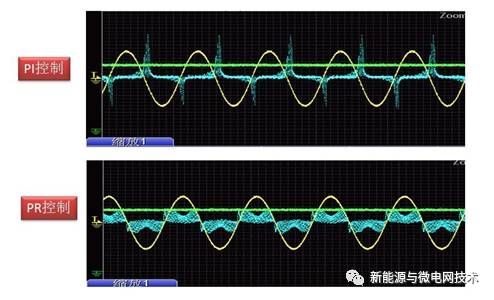
在 PI 调节器的控制下，波形的基波分量已经偏离给定正弦波太多，而 PR 调节器控制下， 电流的基波分量仍然跟随给定信号。

BUS 电压环设计 

在确定好内环的调节器参数之后，可以设计母线外环了，母线外环的设计需要注意一点，单相光伏并网逆变器与功率因数校正电路（PFC）有相似的地方，就是流入电网（PFC  电路是流出电网）的电流必须为正弦，因此母线环的设计就不能将带宽设计的太高。先把控制框图PO 上再说：

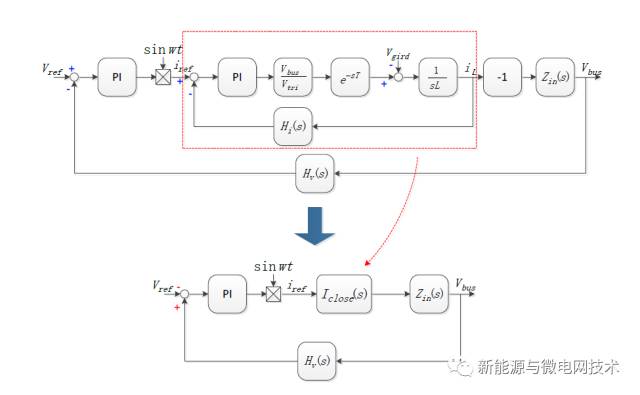
电流环设计好之后可以合并为一个环节。整个框图就会简化为图中下面的框图。首先明确一点，由于并网功率的脉动（50HZ 电压乘以 50Hz 电流，所以交流功率为 100Hz的脉动功率），导致中间母线上出现 100Hz 的纹波（即二次纹波），而这个二次纹波会影响到 并网电流的谐波，导致并网电流中出现严重的 3 次谐波，也是导致并网电流 THD 大的主要原 因。从控制框图可以中看出，bus 电压环的调节器输出再乘以单位正弦信号 sinwt 就是电流环 的参考输入，那么这个 bus 电压环调节器输出中如果含有 2 次纹波，那么电流环的参考输入 信号中就会含有 3 次谐波。这个 3 次谐波是电流环的调节器如何设计都去不掉的，因为它在 给定的参考信号里。

所以从并网电流的 THD 的角度来考虑，最理想的情况就是 bus 电压环的 PI 调节器输出 为一个平直的信号。而从控制框图中我们可以看到，BUS 的参考信号是给定的定值，没有问 题，但是 BUS 的采样反馈信号是含有 2 次纹波的，它们的差值也是含有 2 次纹波的，所以这 就需要 BUS 的调节器能够滤除差值信号中的 2 次纹波（调节器的实质就是一个滤波器），2 次 纹波通常是 100Hz，所以 BUS 的 PI 调节器的带宽不能高于 100Hz，为了滤除 100Hz，通常 设定在 50Hz 以下。那么这样 BUS 环的调节器带宽很低，增益必然也很低，所以 BUS 的动态 响应必然不会快，稳态误差有可能也会受到影响。

一般情况下，就只能面对这个现实了，呵呵，在追求输出电流 THD 的是时候就要牺牲母 线环路的带宽和增益，万事没有完美，大家懂的。

即便输出电流 3 次谐波与母线环带宽增益不可兼得，那也不可任之妄为，对不对！数字控 制嘛，只要中断时间还有，只要 ROM 还能放得下，那就要争取最后一丝希望，没羞没臊的干下去~~~ 

母线环不甘心那么点点带宽和增益，不然母线稳不住，大局 hold 不住，肿么办？不就是 个 2 次纹波么，单挑它！

前面说了 PR 调节器可以单独提高 50Hz 的增益，那么现在我们用个陷波器，单独滤除 100Hz 的增益。陷波器是个虾米玩意呢？实际就是个带阻滤波器，他的传递函数以及 bode 图如下：fc 为陷波器的中心频率，fb 为陷波的宽度。

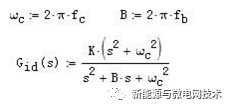
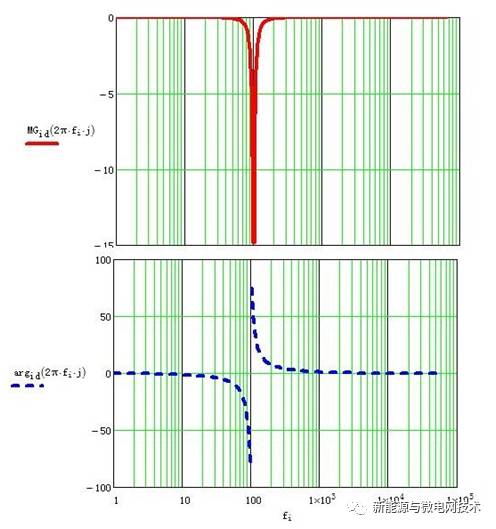
把这个环节加在 BUS 环的 PI 调节器之后，和 sinwt 相乘的信号之前。就可以把电流环给 定中的 3 次谐波大大减小。（因为 2 次纹波乘以 sinwt，出来就是 3 次谐波）。

本来这个也要有仿真波形和实验波形对比，但是我把实验的波形搞丢了，没找到，现在机 器也不在我手里啦，也不能现取波形了，但是我有仿真波形验证，呵呵！

首先来不加陷波器时候的电流波形以及其 THD 分析：红色为电感电流波形，蓝色为电流 参考信号波形；可以看出正弦波稍微有点“偏头”，这实际就是由于 3 次谐波稍大，右下角的可 以看到 THD 为 6.2%左右（感觉 THD 挺大是不，呵呵，因为仿真的 THD 分析是一直分析到 500kHz，大约 1 万次谐波，而实验中 THD 一般分析到 50 次左右。）

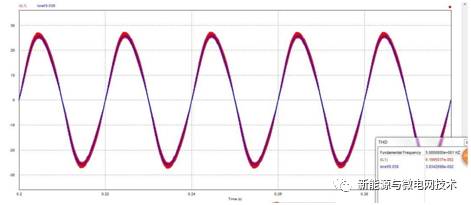
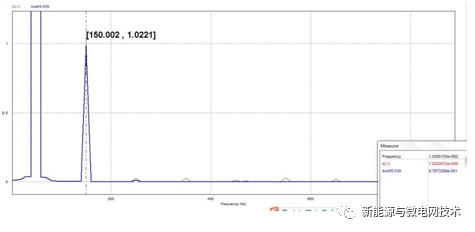
下面的波形是加入陷波器之后的仿真结果：波形“偏头”不明显了，从右下角可以看到 THD 为 4.7%左右

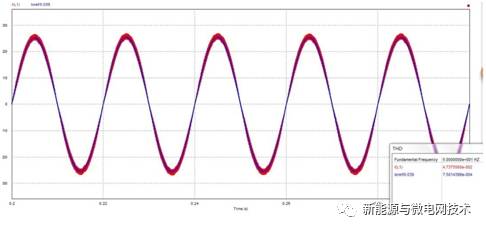
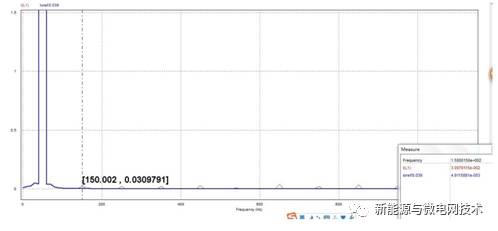
当然有的童鞋会说，我没用你所谓的陷波器，电流也没有这么偏头的厉害。我前面说过， 疯狂降低 BUS 环路的增益和带宽，是可以实现对电流环 3 次谐波的抑制的。

当然所有事情有得必有失，无论 PR 调节器还是陷波器，都对 DSP 的能力（精度和运算 速度）要求比较高。

电网前馈的问题 

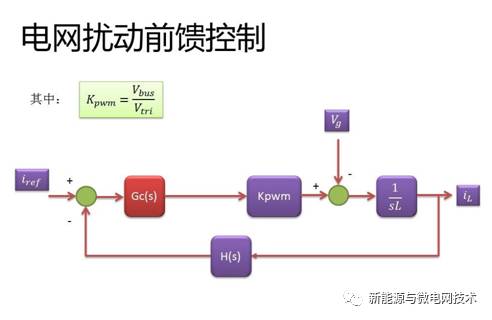
通常单相光伏并网逆变器的控制中会加入电网前馈控制，用来尽快抵消电网的扰动对电流环的影响。我们先来从控制的角度看一下电网扰动带来的误差影响：下面是电流环的控制框图，

其中电网 Vg 的影响位置如图所示：其中 Vg 就是框图中的 N(s)，误差 En(s)为参考信号与反 馈信号之差。

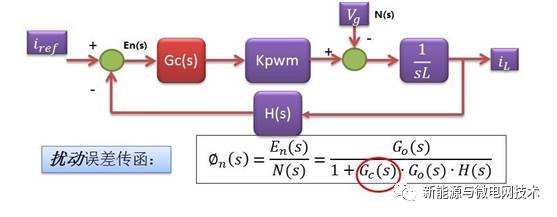
将参数代入后可以得到 220Vac 电网扰动下的误差 bode 图：在 50Hz 处，扰动增益较大。从上面的图中可以看到控制器 Gc 的增益可以影响误差信号，也就是说增大控制器 Gc 在增益 就可以减小误差。

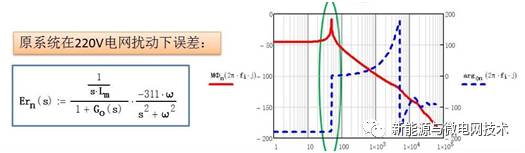
顺便从 bode 图上对比一下电流环 PI 控制器和 PR 控制器对扰动误差的影响：

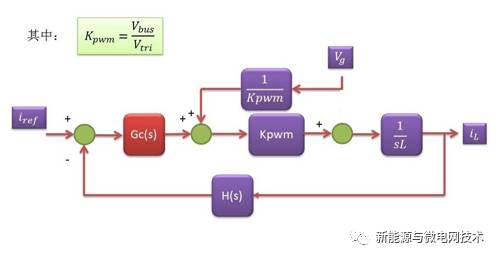
为了快速抑制电网扰动对电流环的影响，很好的办法就是将电网电网信号前馈。我们从控 制框图上来解释一下：第一个图所示为电网扰动的实际位置，根据方框图的变换法则，在第 2 个图的位置加入这个信号，就可以与原来的信号相抵消。这就是前馈的做法。在实际操作中就 是：电网*载波幅值/母线电压，将这个结果加在 PI 调节器的输出上面。

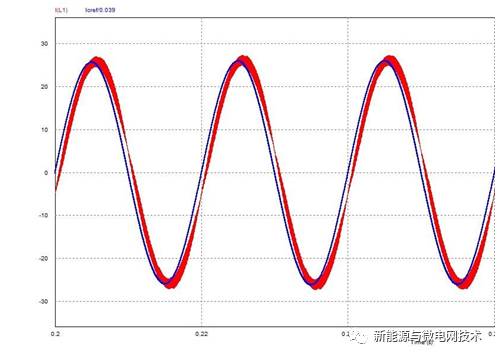
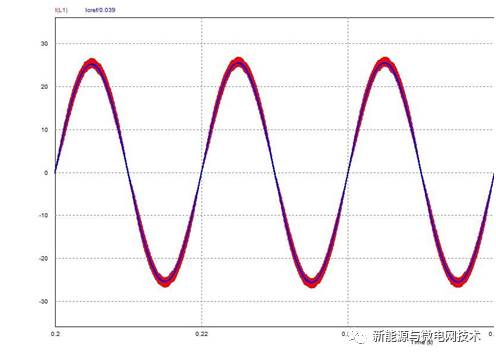
同样我们进行一下仿真验证，电流环统一用 PI 调节器控制：第 1 图为无电网前馈，第 2图为有电网前馈，效果显而易见。（蓝色为给定的电流参考信号，红色为电感电流信号）

控制器的离散化

在用 DSP 实现数字控制的时候，要把控制的部分写成代码才能实现，所以需要把控制器 或者滤波器写成数字控制器或者数字滤波器，也就是离散化。很多初学宝宝估计把控制书上的 离散化过程看了好多遍还是不知道在实际操作中怎么把一个传递函数变成程序代码。今天就把 自己做数字控制时候的转换方法给大家说一下。

首先要明确一点，任何调节器、滤波器离散化成为代码的时候都是固定的格式，就是如下， 根据不同的传递函数，其中有些系数有可能是相同的：

y(n) = k1*y(n-1) + k2*y(n-2) + ... + kN*y(n-N) + kN+1*e(n) + kN+2*e(n-1) + ... + kN+N*e(n-N)

其中 y(n)为调节器的最新输出，y(n-1)、y(n-2)为前一次、前 2 次的输出。

其中 e(n)为调节器的最新输入（参考-反馈的误差），e(n-1)、e(n-2)为前一次、前 2 次的 输入。

具体要取到多少旧值，取决于调节器或者滤波器传递函数 s 的最高次幂。

然后要在每次计算之后更新旧值,例如：

y(n-2) = y(n-1);

y(n-1) = y(n);

e(n-2) = e(n-1);

e(n-1) = e(n);

离散化的方法通常用的有 3 种：

1、差分变换法

2、零阶保持器法

3、双线性变换法

在这里我不讲这三种方法的原理，因为教科书上面都有。我只以 PI 调节器为例，分别说 明这三种方法怎么用。