

神经架构搜索详解
电子说
描述
近期谷歌大脑团队发布了一项新研究:只靠神经网络架构搜索出的网络,不训练,不调参,就能直接执行任务。
这样的网络叫做WANN,权重不可知神经网络。前一阵子在业内引起了不小轰动。
很多同学对其中的关键方法“神经网络架构搜索(NAS)“表现出了极大兴趣。那么什么是NAS呢?
谷歌CEO Sundar Pichai曾表示:“设计神经网络非常耗时,需要具有专门背景知识的人,并且,对专业知识的高要求限制了创业公司和小的社区使用它。
而使用“神经网络设计神经网络”的方法被称为神经结构搜索(NAS),通常使用强化学习或进化算法来设计新的神经网络结构。
关于NAS,原理是什么?初学者又该如何入门?
图灵君对下面这篇选自medium技术博客进行了编译,该文章全面介绍NAS的原理和三种不同方法,希望大家有所帮助。
以下是博文内容:
我们大多数人可能都对ResNet耳熟能详,它是ILSVRC 2015在图像分类、检测和本地化方面的赢家,也是MS COCO 2015检测和分割的赢家。ResNet是一个巨大的架构,遍布各种跳跃连接。当我使用这个ResNet作为自己机器学习项目的预训练网络时,我想的是“怎么会有人提出这样的体系结构呢?”'
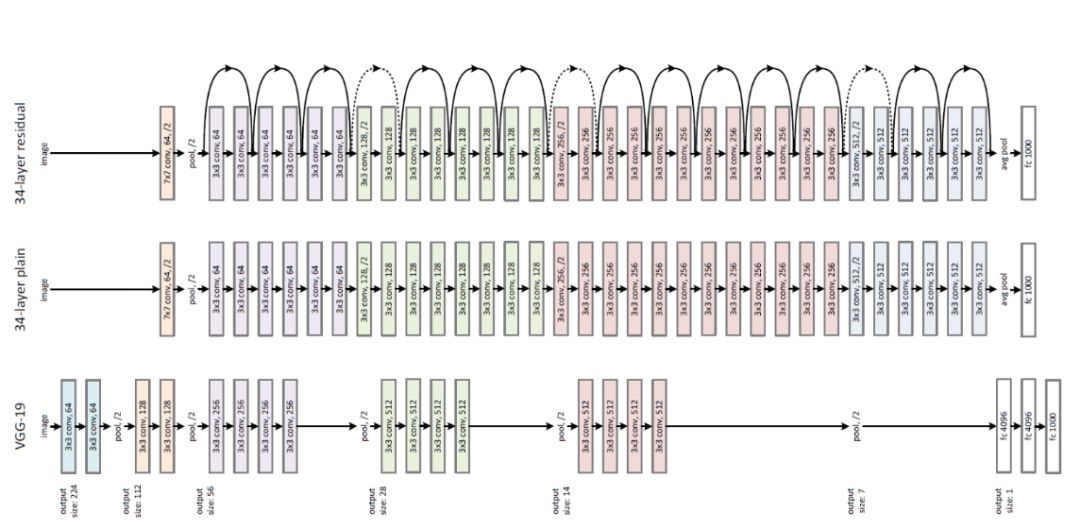
大型人类工程图像分类体系机构
不久之后,我了解到许多工程师和科学家用他们多年的经验构建了这种架构后。并且还有更多的直觉而不是完整的数学将告诉你“我们现在需要一个5x5过滤器以达到最佳精度”。我们有很好的图像分类任务架构,但像我这样的许多年轻学习者通常花费数小时的时间来修复体系结构,同时处理那些不是Image的数据集。我们当然希望别人能为我们做这件事。
因此神经架构搜索(NAS),自动化架构工程的过程就出现了。我们只需要为NAS系统提供数据集,它将为我们提供该数据集的最佳架构。NAS可以被视为AutoML的子域,并且与超参数优化具有明显的重叠。要了解NAS,我们需要深入研究它在做什么。它通过遵循最大化性能的搜索策略,从所有可能的架构中找到架构。下图总结了NAS算法。
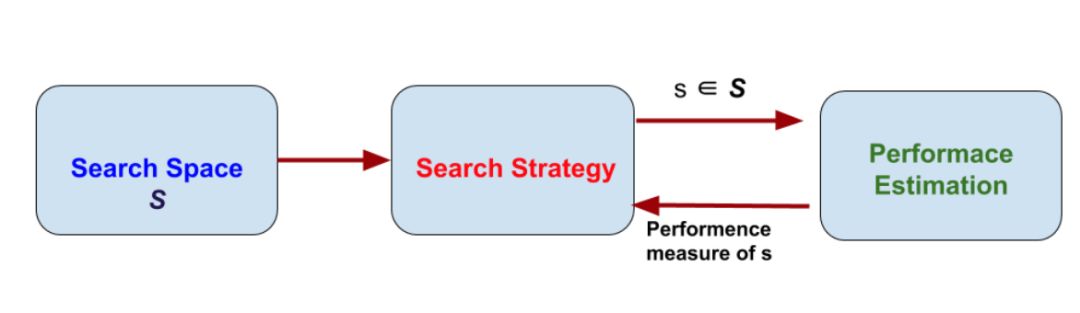
NAS方法的维度
它有3个独立的维度:搜索空间、搜索策略和性能评估。
搜索空间定义了NAS方法原则上可能发现的神经架构。它可以是链状结构,其中层(n-1)的输出作为层(n)的输入馈送。或者它可以是具有跳跃连接(多分支网络)的现代复杂架构。
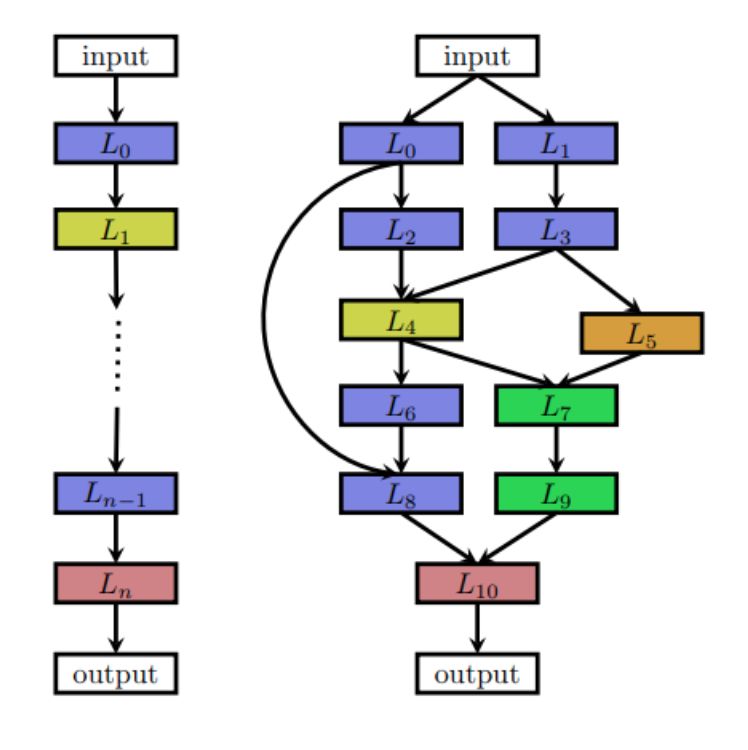
链状网络和多分支网络
有时人们确实想要使用具有重复主题或单元的手工制作的外部架构(宏观架构)。在这种情况下,外部结构是固定的,NAS仅搜索单元体系结构。这种类型的搜索称为微搜索或单元搜索。
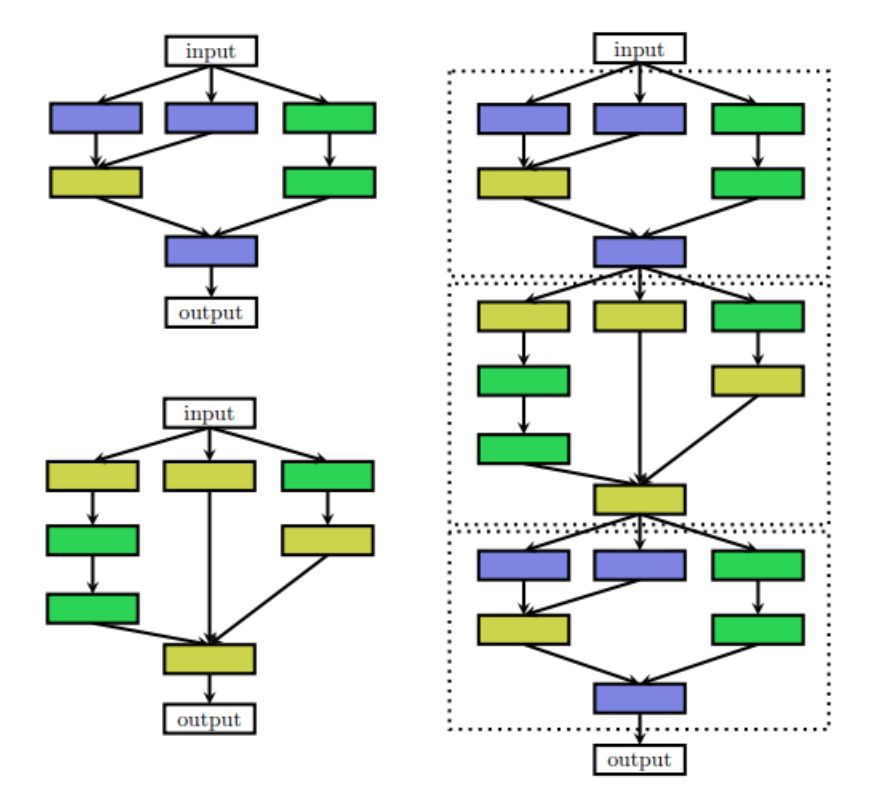
左:单元结构 右:单元放入手工制作的外部结构中
在许多NAS方法中,以分层方式搜索微观和宏观结构; 它由几个层次的主题组成。第一级由原始操作组成,第二级是不同的主题,通过有向无环图连接原始操作,第三级是编码如何连接二级图案的主题,依此类推。
为了解释搜索策略和性能估计,下面将讨论三种不同的NAS方法。
强化学习
我们了解强化学习; 其中根据θ参数化的一些策略执行某些操作。然后,代理从所采取的操作的奖励更新策略θ。在NAS的情况下,代理生成模型体系结构,子网络(动作)。然后在数据集上训练模型,并将模型对验证数据的性能作为奖励。
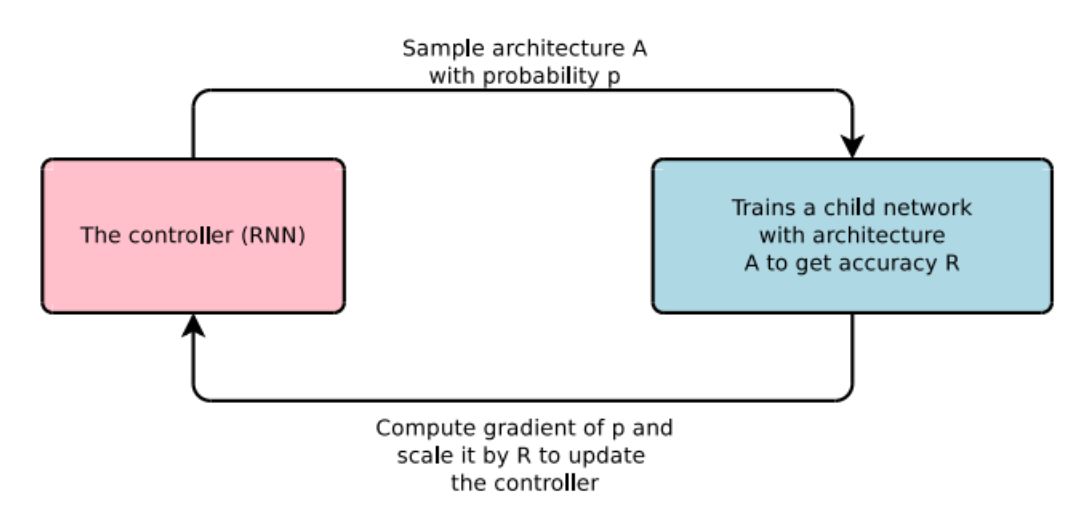
控制器扮演代理的角色,准确性被作为奖励
通常,递归神经网络(RNN)被视为控制器或代理。它产生字符串,模型是随机构建的字符串形式。
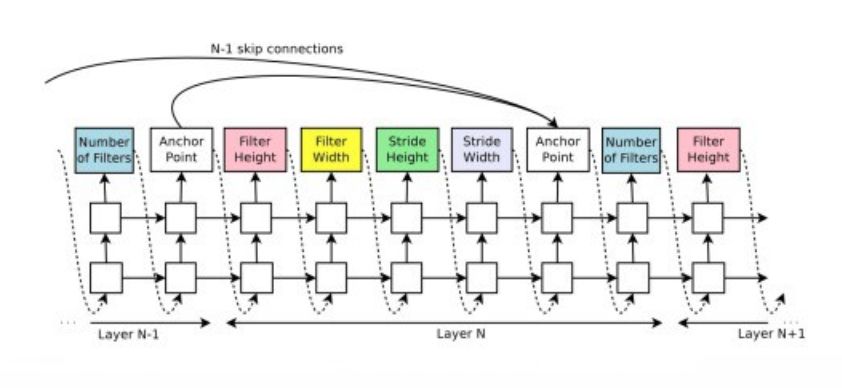
RNN用于创建模型的字符串示例
例如,在图5中,连续的RNN输出用于构建滤波器; 从过滤器高度开始到步宽。输出锚点用于指示跳跃连接。在第N层,锚点将包含N-1个基于内容的sigmoids,以指示需要连接的先前层。
通过策略梯度方法训练RNN以迭代地更新策略θ。这里省略了详细的计算,可以在原始论文的第3.2节中找到。
论文地址:
https://openreview.net/pdf?id=r1Ue8Hcxg
渐进式神经架构搜索(PNAS)
PNAS执行本教程的搜索空间部分中讨论的单元搜索。他们通过以预定义的方式添加单元来构建来自块的单元并构建完整网络。

单元以预定数量串联连接以形成网络。并且每个单元由几个块(原文中使用的5个)形成。

这些块由预定义的操作组成。

块的结构。组合函数只是逐元素相加
操作结果表明,图中所示为原论文所使用的图形,可以进行扩展。
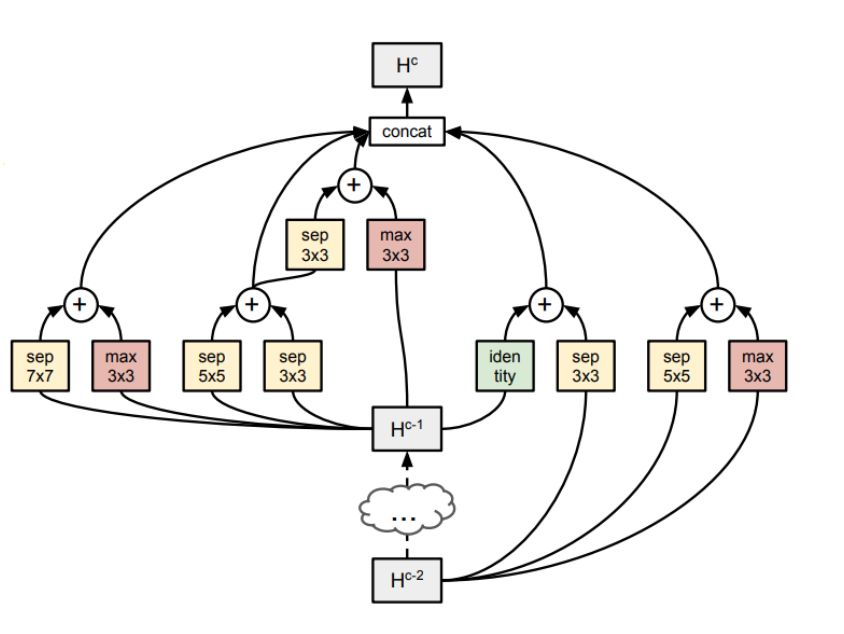
上图显示了完整的示例。即使在这种单元胞或微搜索中,也有10¹⁴个有效组合来检查以找到最佳单元结构。
因此,为了降低复杂性,首先仅构建仅具有1个块的单元。这很容易,因为通过上述操作,只有256个不同的单元是可能的。然后选择顶部K表现最佳的单元以扩展2个块单元,并重复最多5个块。
但是,对于一个合理的K,太多的2块候选来训练。作为这个问题的解决方案,我们训练了仅通过读取字符串(单元被编码成字符串)来预测最终性能的“廉价”代理模型。这种训练的数据是在单元构建、训练和验证时收集的。
例如,我们可以构造所有256个单块单元并测量它们的性能。并使用这些数据训练代理模型。然后使用此模型预测2个块单元的性能,而无需实际训练和测试它们。当然,代理模型应该能够处理可变大小的输入。
然后选择由模型预测的顶部K表现最佳的2个块单元。然后对这2个块单元进行实际训练,对“替代”模型进行微调,并将这些单元扩展为3个块并对其进行迭代
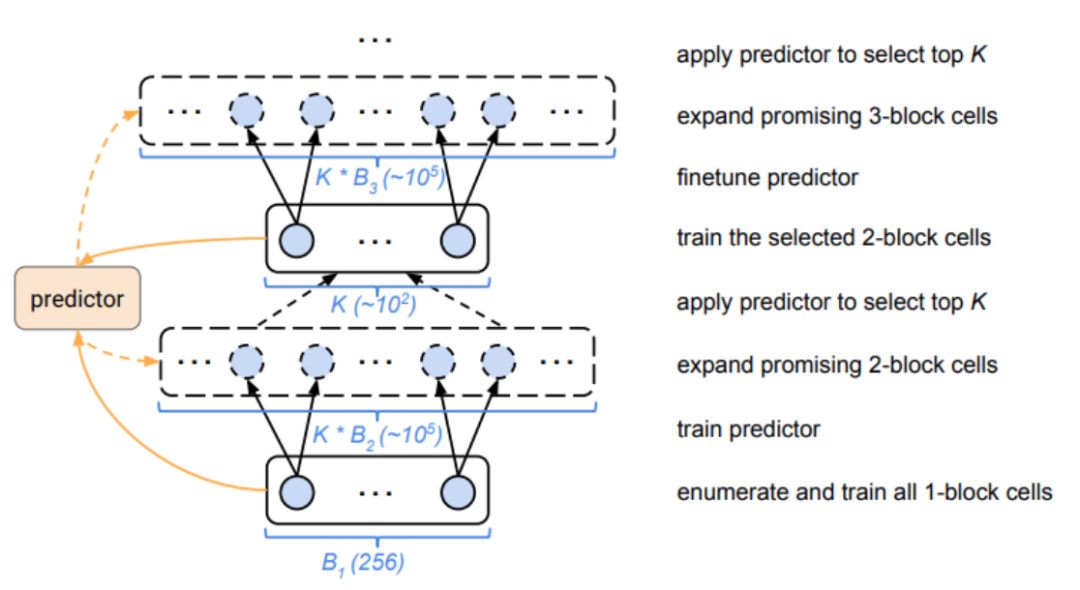
PNAS的步骤
差异化架构搜索(DARTS)
用于神经架构的搜索空间是离散的,即一种架构与另一种架构的不同之处至少在于该架构中有一层或一些参数,例如,5x5滤波器对7x7滤波器。在该方法中,采用连续松弛法进行离散搜索,以实现基于梯度的直接优化。
我们搜索的单元可以是有向无环图,其中每个节点x是潜在表示(例如卷积网络中的特征映射),并且每个有向边(i,j)与某些操作o(i,j)相关联( 卷积,最大池化等,转换x(i)并在节点x(j)处存储潜在表示。
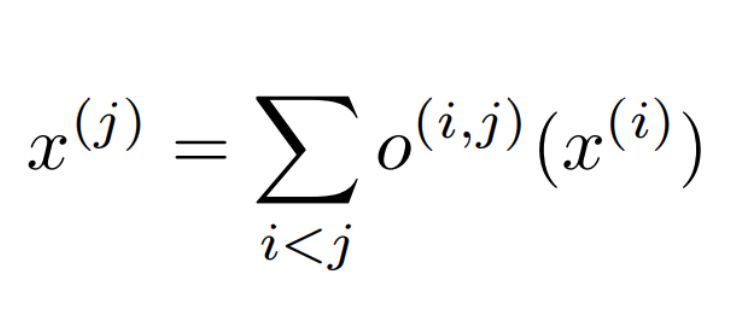
每个节点的输出可以通过上述的等式计算。以这样的方式枚举节点,即从节点x(i)到x(j)存在边(i,j),然后i
在连续松弛法中,不是在两个节点之间进行单个操作。使用每种可能操作的凸组合。为了在图中对此进行建模,保持两个节点之间的多个边缘,每个边缘对应于特定操作。并且每个边缘也具有权重α。
离散问题的连续松弛
现在O(i,j)节点x(i)和x(j)之间的操作是一组操作o(i,j)的凸组合,其中o(.)εS,其中S是所有的集合可能的操作。
O(i,j)的输出由上述方程计算。
L_train和L_val分别表示训练和验证损失。两种损失不仅由架构参数α确定,而且还由网络中的权重“w”确定。架构搜索的目标是找到最小化验证损失L_val(w *,α*)的α*,其中通过最小化训练损失来获得与架构相关联的权重'w *'。
w∗ = argmin L_train(w, α∗ ).
这意味着一个双层优化问题,α作为上层变量,w作为下层变量:
α * = argmin L_val(w ∗ (α), α)
s.t. w ∗ (α) = argmin L_train(w, α)
训练后,某些边的α变得比其他边大得多。为了得到这个连续模型的离散架构,在两个节点之间保留唯一具有最大权重的边。
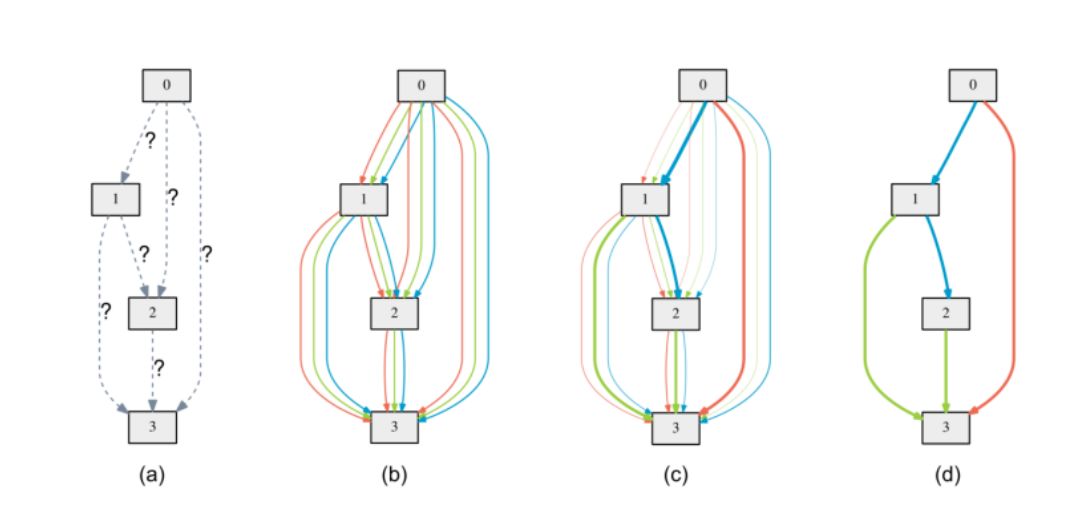
a)上的操作最初是未知的。b)通过在每个边上放置候选操作的混合来连续放松搜索空间c)在双层优化期间一些权重增加并且一些权重下降d)最终体系结构仅通过采用具有两个节点之间的最大权重的边来构建。
当找到单元时,这些单元然后用于构建更大的网络。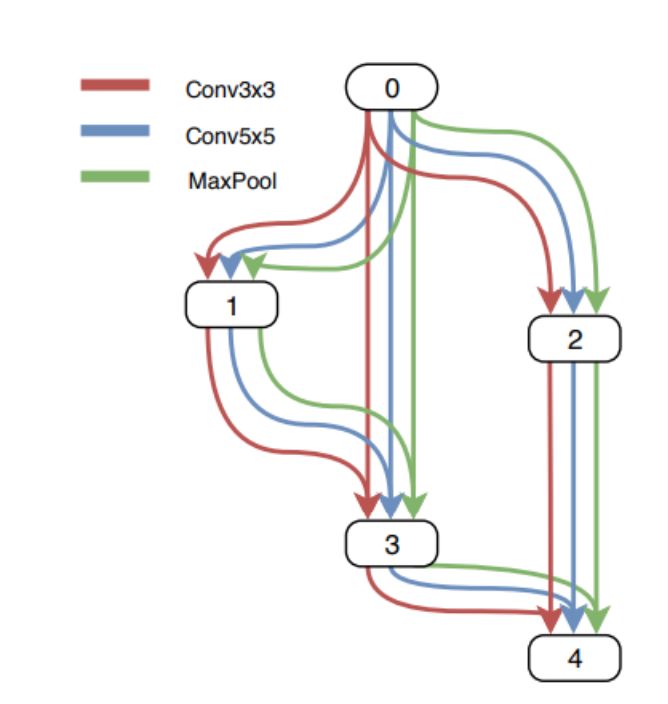

-
神经网络架构有哪些2024-07-01 2315
-
ARM Cortex-M系列芯片神经网络推理库CMSIS-NN详解2022-08-19 4623
-
以进化算法为搜索策略实现神经架构搜索的方法2021-03-22 1405
-
华人团队打造专为GAN量身定制架构搜索方案AutoGAN2020-11-30 1925
-
AutoML和神经架构搜索介绍2019-09-04 2904
-
MIT研发“神经架构搜索”算法,将AI优化的AI设计过程加速240倍或更多2019-04-15 4007
-
神经架构搜索的算法,可以使被AI优化过的AI设计过程加速240多倍2019-04-10 3443
-
一种利用强化学习来设计mobile CNN模型的自动神经结构搜索方法2018-08-07 4766
-
一种新的高效神经架构搜索方法,解决了当前网络变换方法的局限性2018-07-24 7920
-
什么是神经架构搜索?机器学习自动化真能普及大众吗?2018-07-19 6059
-
关于Instgram的搜索架构简要分析2017-10-10 723
-
OpenStack Swift架构详解2012-09-11 13140
-
单片机程序架构详解篇2012-08-17 6427
-
人肉搜索详解2009-08-06 3626
全部0条评论

快来发表一下你的评论吧 !

