基于FPGA的横向FIR滤波器设计详解

关于FIR滤波器的设计，大多数文献和资料都偏向于理论的介绍与阐述，使读者在学习完这类文献后只是明白了如何解决例题与习题，真正的动手设计FIR滤波器依然会觉得抽象很陌生，本文则是在理论的基础上详细阐述了如何基于Verilog HDL搭建的数字电路，来完成来完成FIR横向滤波器的设计。

横向FIR滤波器的设计

设经过AD采集得到的输入序列为x(n)，其通过单位冲激响应为h(n)的因果FIR滤波器后，输出y(n)在时域可表示为线性卷积和的形式：

其中N-1为FIR滤波器阶数（也称抽头数），可以明显的看出h(n)是长度为抽头数加一的有限长序列，不失一般性的设抽头数为3的FIR单位冲激响应h(n)为，

依卷积和画出信号流程图如下，

我们必须明确这里的自变量n表示的并非是连续时间，而是第N次AD采样。

首先根据流程图所示，我们需要设计一个关于x(n)的移位电路，其RTL视图如下，

如图所示的x(n)的移位功能在Verilog中可以通过如下代码实现，注意clk是与数据同步的AD的采样率时钟（AD当前数据建立后，采用一个脉冲标志可实现）。

input clk;input signed[8:0] x_in;output reg signed [8:0] xn;output reg signed [8:0] xn_1;output reg signed [8:0] xn_2;output reg signed [8:0] xn_3;always@(posedge clk)	begin		xn   <= x_in;	//x(n)		xn_1 <= xn;	//x(n-1)		xn_2 <= xn_1;	//x(n-2)		xn_3 <= xn_2;	//x(n-3)	end

 

其次，为了设计方便，需要将浮点数转换为定点运算，注意，N位的数据完成N*N乘法后，其结果的长度为2N位，为了配合乘法运算，我们需要采用18位补码表示有符号数据（MSB为符号位），并对浮点数进行8位的量化处理（乘以256转换为定点数运算，运算结果除以256可得到相应的浮点数），那么上述的系统的冲激响应h(n)可表示为（这里不可避免的引入了量化误差），

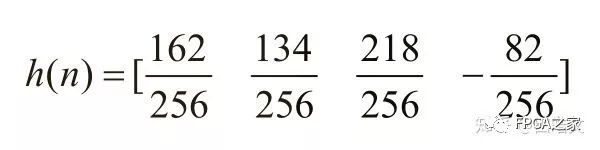
对应的18位补码有符号十进制数为，

电路RTL视图如下，

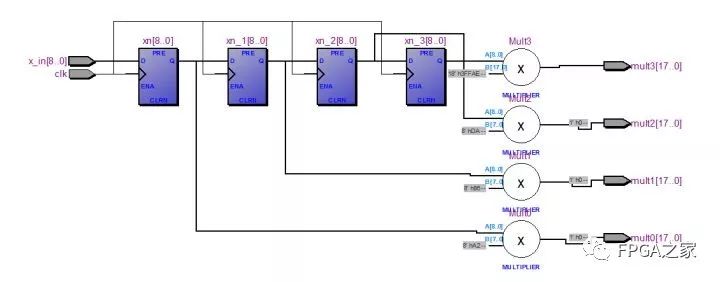
如图所示的x(n)移位后对应的乘法功能在Verilog中可以通过如下代码实现。

input clk;input signed[8:0] x_in;output signed [17:0] mult0;output signed [17:0] mult1;output signed [17:0] mult2;output signed [17:0] mult3;reg signed [8:0] xn;reg signed [8:0] xn_1;reg signed [8:0] xn_2;reg signed [8:0] xn_3;always@(posedge clk)	begin		xn   <= x_in;		//x(n)		xn_1 <= xn;		//x(n-1)		xn_2 <= xn_1;		//x(n-2)		xn_3 <= xn_2;		//x(n-3)		endassign mult0 = xn * 18'd162;	//x(n)  *h(0)assign mult1 = xn_1 * 18'd134;	//x(n-1)*h(1)assign mult2 = xn_2 * 18'd218;	//x(n-2)*h(2)assign mult3 = xn_3 * 18'd262062;//x(n-3)*h(3)

 

最后，采用一级加法电路完成整个求卷积和的过程，需要注意的是，有符号的加法操作，需要对符合位进行保护，完成加法后数据的长度应设为2*N+log2(Tap+1)-1(其中Tap表示抽头数)，则本文需要的加法寄存器的长度为为19位（2*9+log(4)-1），并且取其高11位作为y(n)输出（该操作等于除以256）其电路RTL视图如下，

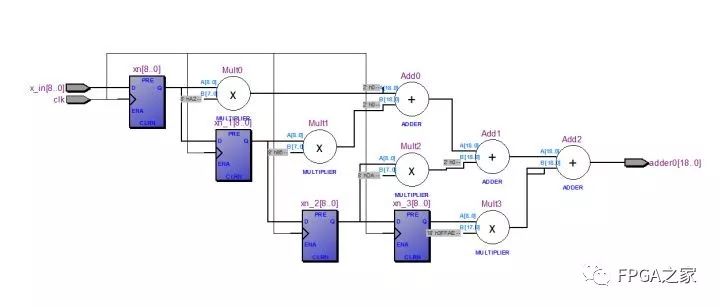
该结构的总体Verilog代码如下。

module fir(	input clk,	input signed[8:0] x_in,	output signed [10:0] y_out);reg signed [8:0] xn;reg signed [8:0] xn_1;reg signed [8:0] xn_2;reg signed [8:0] xn_3;wire signed [17:0] mult0;wire signed [17:0] mult1;wire signed [17:0] mult2;wire signed [17:0] mult3;wire signed [18:0] adder0;always@(posedge clk)	begin		xn   <= x_in;		//x(n)		xn_1 <= xn;			//x(n-1)		xn_2 <= xn_1;		//x(n-2)		xn_3 <= xn_2;		//x(n-3)		endassign mult0 = xn * 18'd162;		//x(n)  *h(0)assign mult1 = xn_1 * 18'd134;	//x(n-1)*h(1)assign mult2 = xn_2 * 18'd218;	//x(n-2)*h(2)assign mult3 = xn_3 * 18'd262062;//x(n-3)*h(3)	assign adder0 = mult0 + mult1 + mult2 + mult3; //adder0(n)=x(n)*h(0)+x(n-1)*h(1)+x(n-2)*h(2)+x(n-3)*h(3)assign y_out = adder0[18:8];	//y(n)=adder0(n)/256endmodule

 

基于ModelSim求系统冲激响应与矩形脉冲响应

列写testbench如下，

`timescale 1ns/1ns`define ad_clk 20module fir_tb;	reg						clk;	reg signed[8:0] 		x_in;	wire signed [10:0] 	y_out;		fir fir(		.clk(clk),		.x_in(x_in),		.y_out(y_out)	);	initial clk = 1;	always#(`ad_clk/2) clk = ~clk;		initial		begin			x_in = 9'd0;			#(`ad_clk*20);			#3;			x_in = 9'd100;			#(`ad_clk);			x_in = 9'd0;			#(`ad_clk*20);			x_in = 9'd100;			#(`ad_clk);			x_in = 9'd100;			#(`ad_clk);			x_in = 9'd100;			#(`ad_clk);			x_in = 9'd100;			#(`ad_clk);			x_in = 9'd100;			#(`ad_clk);			x_in = 9'd0;			#(`ad_clk*20);				$stop;			endendmodule

 

仿真求得对应的响应为

显然，当输入为x(n)=100δ(n)时,输出为y(n)=100h(n)（存在着量化误差），输入为x(n)=100[u(n)-u(n-5)]时，输出y(n)=[63δ(n) 115δ(n-1) 200δ(n-2) 168δ(n-3) 168δ(n-4) 105δ(n-5) 53δ(n-6) -33δ(n-7)]。