在kaggle的竞赛中，参赛者取得top0.3%的经验和技巧

导读：刚开始接触数据竞赛时，我们可能会被一些高大上的技术吓到。各界大佬云集，各种技术令人眼花缭乱，新手们就像蜉蝣一般渺小无助。今天本文就分享一下在 kaggle 的竞赛中，参赛者取得 top0.3% 的经验和技巧。让我们开始吧！

Top 0.3% 模型概览

赛题和目标

数据集中的每一行都描述了某一匹马的特征

在已知这些特征的条件下，预测每匹马的销售价格

预测价格对数和真实价格对数的RMSE（均方根误差）作为模型的评估指标。将RMSE转化为对数尺度，能够保证廉价马匹和高价马匹的预测误差，对模型分数的影响较为一致。

模型训练过程中的重要细节

交叉验证：使用12-折交叉验证

模型：在每次交叉验证中，同时训练七个模型（ridge, svr, gradient boosting, random forest, xgboost, lightgbm regressors）

Stacking 方法：使用 xgboot 训练了元 StackingCVRegressor 学习器

模型融合：所有训练的模型都会在不同程度上过拟合，因此，为了做出最终的预测，将这些模型进行了融合，得到了鲁棒性更强的预测结果

模型性能

从下图可以看出，融合后的模型性能最好，RMSE 仅为 0.075，该融合模型用于最终预测。

In[1]：

from IPython.display import ImageImage("../input/kernel-files/model_training_advanced_regression.png")

Output[1]：

现在让我们正式开始吧！

In[2]：

# Essentialsimport numpy as npimport pandas as pdimport datetimeimport random

# Plotsimport seaborn as snsimport matplotlib.pyplot as plt# Modelsfrom sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, AdaBoostRegressor, BaggingRegressorfrom sklearn.kernel_ridge import KernelRidgefrom sklearn.linear_model import Ridge, RidgeCVfrom sklearn.linear_model import ElasticNet, ElasticNetCVfrom sklearn.svm import SVRfrom mlxtend.regressor import StackingCVRegressorimport lightgbm as lgbfrom lightgbm import LGBMRegressorfrom xgboost import XGBRegressor# Statsfrom scipy.stats import skew, normfrom scipy.special import boxcox1pfrom scipy.stats import boxcox_normmax# Miscfrom sklearn.model_selection import GridSearchCVfrom sklearn.model_selection import KFold, cross_val_scorefrom sklearn.metrics import mean_squared_errorfrom sklearn.preprocessing import OneHotEncoderfrom sklearn.preprocessing import LabelEncoderfrom sklearn.pipeline import make_pipelinefrom sklearn.preprocessing import scalefrom sklearn.preprocessing import StandardScalerfrom sklearn.preprocessing import RobustScalerfrom sklearn.decomposition import PCApd.set_option('display.max_columns', None)# Ignore useless warningsimport warningswarnings.filterwarnings(action="ignore")pd.options.display.max_seq_items = 8000pd.options.display.max_rows = 8000import osprint(os.listdir("../input/kernel-fi

Output[2]：

['model_training_advanced_regression.png']

In[3]：

# Read in the dataset as a dataframetrain = pd.read_csv('../input/house-prices-advanced-regression-techniques/train.csv')test = pd.read_csv('../input/house-prices-advanced-regression-techniques/test.csv')train.shape, test.shape

Output[3]：

((1460, 81), (1459, 80))

EDA

目标

数据集中的每一行都描述了某一匹马的特征

在已知这些特征的条件下，预测每匹马的销售价格

对原始数据进行可视化

In[4]：

# Preview the data we're working withtrain.head()

Output[5]：

SalePrice：目标值的特性探究

In[5]：

sns.set_style("white")sns.set_color_codes(palette='deep')f, ax = plt.subplots(figsize=(8, 7))#Check the new distributionsns.distplot(train['SalePrice'], color="b");ax.xaxis.grid(False)ax.set(ylabel="Frequency")ax.set(xlabel="SalePrice")ax.set(title="SalePrice distribution")sns.despine(trim=True, left=True)plt.show()

In[6]：

# Skew and kurtprint("Skewness: %f" % train['SalePrice'].skew())print("Kurtosis: %f" % train['SalePrice'].kurt())

Skewness: 1.882876

Kurtosis: 6.536282

可用的特征：深入探索

数据可视化

In[7]：

# Finding numeric featuresnumeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']numeric = []for i in train.columns: if train[i].dtype in numeric_dtypes: if i in ['TotalSF', 'Total_Bathrooms','Total_porch_sf','haspool','hasgarage','hasbsmt','hasfireplace']: pass else: numeric.append(i)# visualising some more outliers in the data valuesfig, axs = plt.subplots(ncols=2, nrows=0, figsize=(12, 120))plt.subplots_adjust(right=2)plt.subplots_adjust(top=2)sns.color_palette("husl", 8)for i, feature in enumerate(list(train[numeric]), 1): if(feature=='MiscVal'): break plt.subplot(len(list(numeric)), 3, i) sns.scatterplot(x=feature, y='SalePrice', hue='SalePrice', palette='Blues', data=train) plt.xlabel('{}'.format(feature), size=15,labelpad=12.5) plt.ylabel('SalePrice', size=15, labelpad=12.5) for j in range(2): plt.tick_params(axis='x', labelsize=12) plt.tick_params(axis='y', labelsize=12) plt.legend(loc='best', prop={'size': 10})plt.show()

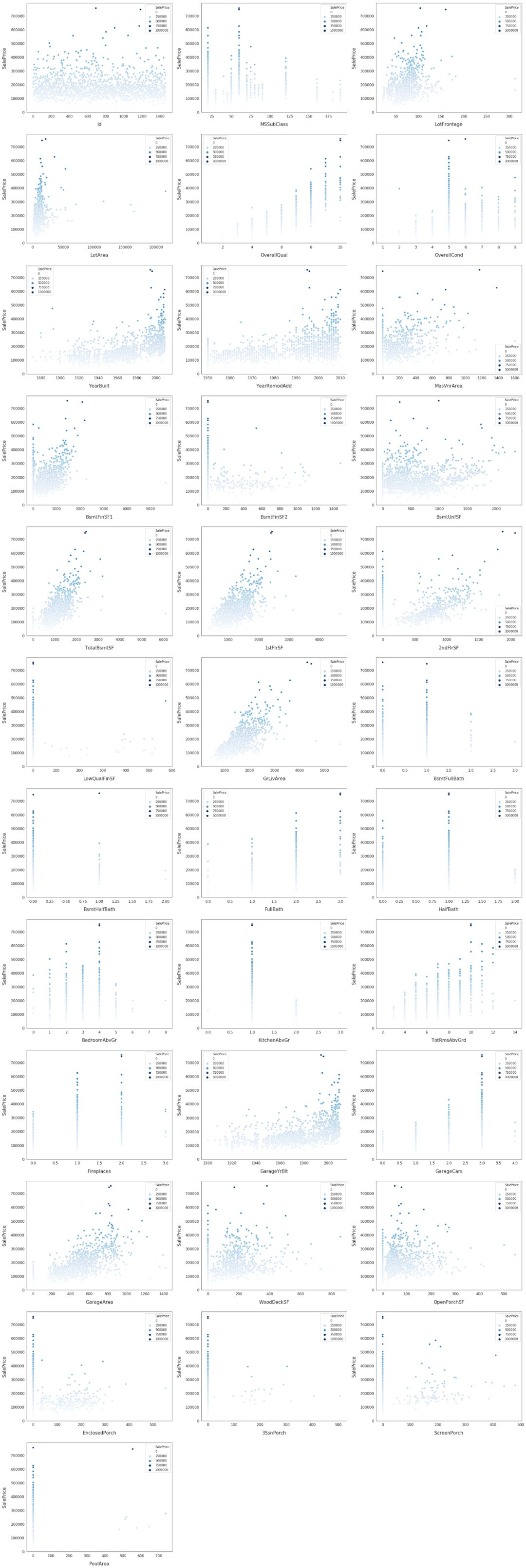
探索这些特征以及 SalePrice 的相关性

In[8]：

corr = train.corr()plt.subplots(figsize=(15,12))sns.heatmap(corr, vmax=0.9, cmap="Blues", square=True)

Output[8]：

       

选取部分特征，可视化它们和 SalePrice 的相关性

Input[9]：

data = pd.concat([train['SalePrice'], train['OverallQual']], axis=1)f, ax = plt.subplots(figsize=(8, 6))fig = sns.boxplot(x=train['OverallQual'], y="SalePrice", data=data)fig.axis(ymin=0, ymax=800000);

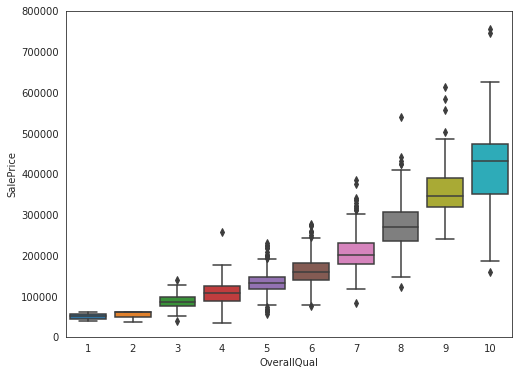
Input[10]：

data = pd.concat([train['SalePrice'], train['YearBuilt']], axis=1)f, ax = plt.subplots(figsize=(16, 8))fig = sns.boxplot(x=train['YearBuilt'], y="SalePrice", data=data)fig.axis(ymin=0, ymax=800000);plt.xticks(rotation=45);

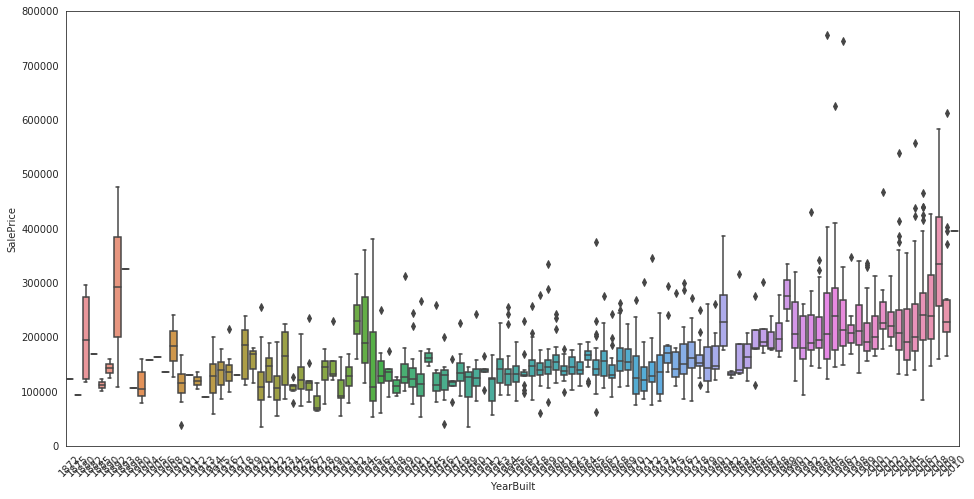
Input[11]：

data = pd.concat([train['SalePrice'], train['TotalBsmtSF']], axis=1)data.plot.scatter(x='TotalBsmtSF', y='SalePrice', alpha=0

.3, ylim=(0,800000));

Input[12]：

data = pd.concat([train['SalePrice'], train['LotArea']], axis=1)data.plot.scatter(x='LotArea', y='SalePrice', alpha=0.3, y

lim=(0,800000));

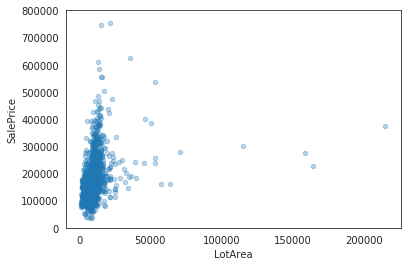
Input[13]：

data = pd.concat([train['SalePrice'], train['GrLivArea']], axis=1)data.plot.scatter(x='GrLivArea', y='SalePrice', alpha=0.3,

ylim=(0,800000));

Input[14]：

# Remove the Ids from train and test, as they are unique for each row and hence not useful for the modeltrain_ID = train['Id']test_ID = test['Id']train.drop(['Id'], axis=1, inplace=True)test.drop(['Id'], axis=1, inplace=True)train.shape, test.shape

Output[14]：

((1460, 80), (1459, 79))

可视化 salePrice 的分布

Input[15]：

sns.set_style("white")sns.set_color_codes(palette='deep')f, ax = plt.subplots(figsize=(8, 7))#Check the new distributionsns.distplot(train['SalePrice'], color="b");ax.xaxis.grid(False)ax.set(ylabel="Frequency")ax.set(xlabel="SalePrice")ax.set(title="SalePrice distribution")sns.despine(trim=True, left=True)plt.show()

从上图中可以看出，SalePrice 有点向右边倾斜，由于大多数机器学习模型对非正态分布的数据的效果不佳，因此，我们对数据进行变换，修正这种倾斜：log(1+x) 

Input[16]：

# log(1+x) transformtrain["SalePrice"] = np.log1p(train["SalePrice"])

对 SalePrice 重新进行可视化

Input[17]：

sns.set_style("white")sns.set_color_codes(palette='deep')f, ax = plt.subplots(figsize=(8, 7))#Check the new distributionsns.distplot(train['SalePrice'] , fit=norm, color="b");# Get the fitted parameters used by the function(mu, sigma) = norm.fit(train['SalePrice'])print( ' mu = {:.2f} and sigma = {:.2f} '.format(mu, sigma))#Now plot the distributionplt.legend(['Normal dist. ($mu=$ {:.2f} and $sigma=$ {:.2f} )'.format(mu, sigma)], loc='best')ax.xaxis.grid(False)ax.set(ylabel="Frequency")ax.set(xlabel="SalePrice")ax.set(title="SalePrice distribution")sns.despine(trim=True, left=True)plt.show

mu = 12.02 and sigma = 0.40

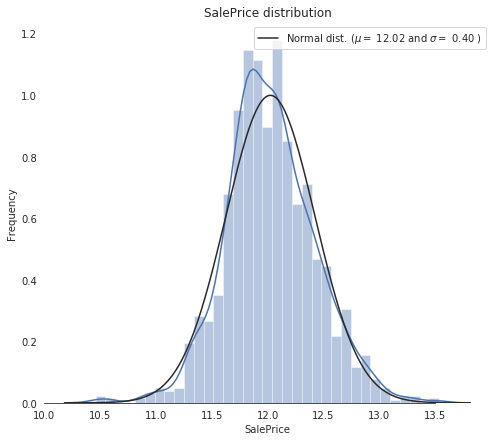
从图中可以看到，当前的 SalePrice 已经变成了正态分布

Input[18]：

# Remove outlierstrain.drop(train[(train['OverallQual']<5) & (train['SalePrice']>200000)].index, inplace=True)train.drop(train[(train['GrLivArea']>4500) & (train['SalePrice']<300000)].index, inplace=True)train.reset_index(drop=True, inplace=True)

Input[19]：

# Split features and labelstrain_labels = train['SalePrice'].reset_index(drop=True)train_features = train.drop(['SalePrice'], axis=1)test_features = test# Combine train and test features in order to apply the feature transformation pipeline to the entire datasetall_features = pd.concat([train_features, test_features]).reset_index(drop=True)all_features.shape

Input[19]：

(2917, 79)

填充缺失值

Input[20]：

# determine the threshold for missing valuesdef percent_missing(df): data = pd.DataFrame(df) df_cols = list(pd.DataFrame(data)) dict_x = {} for i in range(0, len(df_cols)): dict_x.update({df_cols[i]: round(data[df_cols[i]].isnull().mean()*100,2)}) return dict_xmissing = percent_missing(all_features)df_miss = sorted(missing.items(), key=lambda x: x[1], reverse=True)print('Percent of missing data')df_miss[0:10]

Percent of missing data

Output[20]：

[('PoolQC', 99.69),

('MiscFeature', 96.4),

('Alley', 93.21),

('Fence', 80.43),

('FireplaceQu', 48.68),

('LotFrontage', 16.66),

('GarageYrBlt', 5.45),

('GarageFinish', 5.45),

('GarageQual', 5.45),

('GarageCond', 5.45)]

Input[21]：

# Visualize missing valuessns.set_style("white")f, ax = plt.subplots(figsize=(8, 7))sns.set_color_codes(palette='deep')missing = round(train.isnull().mean()*100,2)missing = missing[missing > 0]missing.sort_values(inplace=True)missing.plot.bar(color="b")# Tweak the visual presentationax.xaxis.grid(False)ax.set(ylabel="Percent of missing values")ax.set(xlabel="Features")ax.set(title="Percent missing data by feature")sns.despine(trim=True, left=True)

接下来，我们将分别对每一列填充缺失值

Input[22]：

# Some of the non-numeric predictors are stored as numbers; convert them into stringsall_features['MSSubClass'] = all_features['MSSubClass'].apply(str)all_features['YrSold'] = all_features['YrSold'].astype(str)all_features['MoSold'] = all_features['MoSold'].astype(str)

Input[23]：

def handle_missing(features): # the data description states that NA refers to typical ('Typ') values features['Functional'] = features['Functional'].fillna('Typ') # Replace the missing values in each of the columns below with their mode features['Electrical'] = features['Electrical'].fillna("SBrkr") features['KitchenQual'] = features['KitchenQual'].fillna("TA") features['Exterior1st'] = features['Exterior1st'].fillna(features['Exterior1st'].mode()[0]) features['Exterior2nd'] = features['Exterior2nd'].fillna(features['Exterior2nd'].mode()[0]) features['SaleType'] = features['SaleType'].fillna(features['SaleType'].mode()[0]) features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0])) # the data description stats that NA refers to "No Pool" features["PoolQC"] = features["PoolQC"].fillna("None") # Replacing the missing values with 0, since no garage = no cars in garage for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'): features[col] = features[col].fillna(0) # Replacing the missing values with None for col in ['GarageType', 'GarageFinish', 'GarageQual', 'GarageCond']: features[col] = features[col].fillna('None') # NaN values for these categorical basement features, means there's no basement for col in ('BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2'): features[col] = features[col].fillna('None') # Group the by neighborhoods, and fill in missing value by the median LotFrontage of the neighborhood features['LotFrontage'] = features.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median())) # We have no particular intuition around how to fill in the rest of the categorical features # So we replace their missing values with None objects = [] for i in features.columns: if features[i].dtype == object: objects.append(i) features.update(features[objects].fillna('None')) # And we do the same thing for numerical features, but this time with 0s numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64'] numeric = [] for i in features.columns: if features[i].dtype in numeric_dtypes: numeric.append(i) features.update(features[numeric].fillna(0)) return featuresall_features = handle_missing(all_features

Input[24]：

# Let's make sure we handled all the missing valuesmissing = percent_missing(all_features)df_miss = sorted(missing.items(), key=lambda x: x[1], reverse=True)print('Percent of missing data')df_miss[0:10]

Output[14]：

Percent of missing data

[('MSSubClass', 0.0),

('MSZoning', 0.0),

('LotFrontage', 0.0),

('LotArea', 0.0),

('Street', 0.0),

('Alley', 0.0),

('LotShape', 0.0),

('LandContour', 0.0),

('Utilities', 0.0),

('LotConfig', 0.0)]

从上面的结果可以看到，所有缺失值已经填充完毕

调整分布倾斜的特征

Input[25]：

# Fetch all numeric featuresnumeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']numeric = []for i in all_features.columns: if all_features[i].dtype in numeric_dtypes: numeric.append(i)

Input[26]：

# Create box plots for all numeric featuressns.set_style("white")f, ax = plt.subplots(figsize=(8, 7))ax.set_xscale("log")ax = sns.boxplot(data=all_features[numeric] , orient="h", palette="Set1")ax.xaxis.grid(False)ax.set(ylabel="Feature names")ax.set(xlabel="Numeric values")ax.set(title="Numeric Distribution of Features")sns.despine(trim=True, left=True)

Input[27]：

# Find skewed numerical featuresskew_features = all_features[numeric].apply(lambda x: skew(x)).sort_values(ascending=False)high_skew = skew_features[skew_features > 0.5]skew_index = high_skew.indexprint("There are {} numerical features with Skew > 0.5 :".format(high_skew.shape[0]))skewness = pd.DataFrame({'Skew' :high_skew})skew_features.head(10

Output[27]：

There are 25 numerical features with Skew > 0.5 :

MiscVal          21.939672

PoolArea         17.688664

LotArea          13.109495

LowQualFinSF     12.084539

3SsnPorch        11.372080

KitchenAbvGr      4.300550

BsmtFinSF2        4.144503

EnclosedPorch     4.002344

ScreenPorch       3.945101

BsmtHalfBath      3.929996

dtype: float64

使用 scipy 的函数 boxcox1来进行 Box-Cox 转换，将数据正态化

Input[28]：# Normalize skewed featuresfor i in skew_index: all_features[i] = boxcox1p(all_features[i],     boxcox_normmax(all_features[i] + 1))

Input[29]：

# Let's make sure we handled all the skewed valuessns.set_style("white")f, ax = plt.subplots(figsize=(8, 7))ax.set_xscale("log")ax = sns.boxplot(data=all_features[skew_index] , orient="h", palette="Set1")ax.xaxis.grid(False)ax.set(ylabel="Feature names")ax.set(xlabel="Numeric values")ax.set(title="Numeric Distribution of Features")sns.despine(trim=True, left=True)

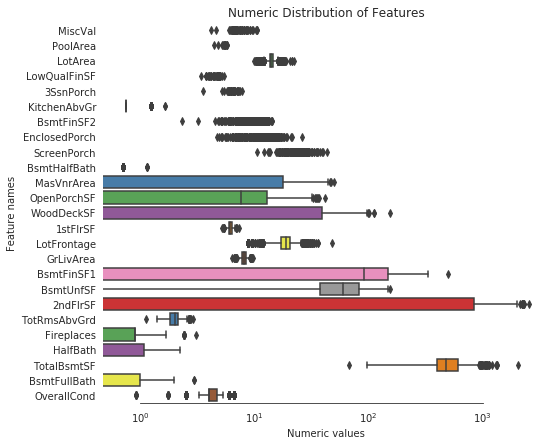
从上图可以看到，所有特征都看上去呈正态分布了。

创建一些有用的特征

机器学习模型对复杂模型的认知较差，因此我们需要用我们的直觉来构建有效的特征，从而帮助模型更加有效的学习。

all_features['BsmtFinType1_Unf'] = 1*(all_features['BsmtFinType1'] == 'Unf')all_features['HasWoodDeck'] = (all_features['WoodDeckSF'] == 0) * 1all_features['HasOpenPorch'] = (all_features['OpenPorchSF'] == 0) * 1all_features['HasEnclosedPorch'] = (all_features['EnclosedPorch'] == 0) * 1all_features['Has3SsnPorch'] = (all_features['3SsnPorch'] == 0) * 1all_features['HasScreenPorch'] = (all_features['ScreenPorch'] == 0) * 1all_features['YearsSinceRemodel'] = all_features['YrSold'].astype(int) - all_features['YearRemodAdd'].astype(int)all_features['Total_Home_Quality'] = all_features['OverallQual'] + all_features['OverallCond']all_features = all_features.drop(['Utilities', 'Street', 'PoolQC',], axis=1)all_features['TotalSF'] = all_features['TotalBsmtSF'] + all_features['1stFlrSF'] + all_features['2ndFlrSF']all_features['YrBltAndRemod'] = all_features['YearBuilt'] + all_features['YearRemodAdd']all_features['Total_sqr_footage'] = (all_features['BsmtFinSF1'] + all_features['BsmtFinSF2'] + all_features['1stFlrSF'] + all_features['2ndFlrSF'])all_features['Total_Bathrooms'] = (all_features['FullBath'] + (0.5 * all_features['HalfBath']) + all_features['BsmtFullBath'] + (0.5 * all_features['BsmtHalfBath']))all_features['Total_porch_sf'] = (all_features['OpenPorchSF'] + all_features['3SsnPorch'] + all_features['EnclosedPorch'] + all_features['ScreenPorch'] + all_features['WoodDeckSF'])all_features['TotalBsmtSF'] = all_features['TotalBsmtSF'].apply(lambda x: np.exp(6) if x <= 0.0 else x)all_features['2ndFlrSF'] = all_features['2ndFlrSF'].apply(lambda x: np.exp(6.5) if x <= 0.0 else x)all_features['GarageArea'] = all_features['GarageArea'].apply(lambda x: np.exp(6) if x <= 0.0 else x)all_features['GarageCars'] = all_features['GarageCars'].apply(lambda x: 0 if x <= 0.0 else x)all_features['LotFrontage'] = all_features['LotFrontage'].apply(lambda x: np.exp(4.2) if x <= 0.0 else x)all_features['MasVnrArea'] = all_features['MasVnrArea'].apply(lambda x: np.exp(4) if x <= 0.0 else x)all_features['BsmtFinSF1'] = all_features['BsmtFinSF1'].apply(lambda x: np.exp(6.5) if x <= 0.0 else x)all_features['haspool'] = all_features['PoolArea'].apply(lambda x: 1 if x > 0 else 0)all_features['has2ndfloor'] = all_features['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)all_features['hasgarage'] = all_features['GarageArea'].apply(lambda x: 1 if x > 0 else 0)all_features['hasbsmt'] = all_features['TotalBsmtSF'].apply(lambda x: 1 if x > 0 else 0)all_features['hasfireplace'] = all_features['Fireplaces'].apply(lambda x: 1 if x > 0 else 0

特征转换

通过对特征取对数或者平方，可以创造更多的特征，这些操作有利于发掘潜在的有用特征。

def logs(res, ls): m = res.shape[1] for l in ls: res = res.assign(newcol=pd.Series(np.log(1.01+res[l])).values) res.columns.values[m] = l + '_log' m += 1 return reslog_features = ['LotFrontage','LotArea','MasVnrArea','BsmtFinSF1','BsmtFinSF2','BsmtUnfSF', 'TotalBsmtSF','1stFlrSF','2ndFlrSF','LowQualFinSF','GrLivArea', 'BsmtFullBath','BsmtHalfBath','FullBath','HalfBath','BedroomAbvGr','KitchenAbvGr', 'TotRmsAbvGrd','Fireplaces','GarageCars','GarageArea','WoodDeckSF','OpenPorchSF', 'EnclosedPorch','3SsnPorch','ScreenPorch','PoolArea','MiscVal','YearRemodAdd','TotalSF']all_features = logs(all_features, log_features

def squares(res, ls): m = res.shape[1] for l in ls: res = res.assign(newcol=pd.Series(res[l]*res[l]).values) res.columns.values[m] = l + '_sq' m += 1 return ressquared_features = ['YearRemodAdd', 'LotFrontage_log', 'TotalBsmtSF_log', '1stFlrSF_log', '2ndFlrSF_log', 'GrLivArea_log', 'GarageCars_log', 'GarageArea_log']all_features = squares(all_features, squared_features)

对集合特征进行编码

对集合特征进行数值编码，使得机器学习模型能够处理这些特征。

all_features = pd.get_dummies(all_features).reset_index(drop=True)all_features.shape

(2917, 379)

all_features.head()

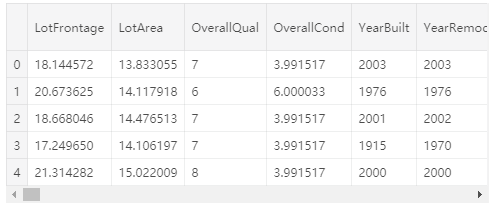
all_features.shape

(2917, 379)

# Remove any duplicated column namesall_features = all_features.loc[:,~all_features.columns. duplicated()]

重新创建训练集和测试集

X = all_features.iloc[:len(train_labels), :]X_test = all_features.iloc[len(train_labels):, :]X.shape, train_labels.shape, X_test.shape

((1458, 378), (1458,), (1459, 378))

对训练集中的部分特征进行可视化

# Finding numeric featuresnumeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']numeric = []for i in X.columns: if X[i].dtype in numeric_dtypes: if i in ['TotalSF', 'Total_Bathrooms','Total_porch_sf','haspool','hasgarage','hasbsmt','hasfireplace']: pass else: numeric.append(i)# visualising some more outliers in the data valuesfig, axs = plt.subplots(ncols=2, nrows=0, figsize=(12, 150))plt.subplots_adjust(right=2)plt.subplots_adjust(top=2)sns.color_palette("husl", 8)for i, feature in enumerate(list(X[numeric]), 1): if(feature=='MiscVal'): break plt.subplot(len(list(numeric)), 3, i) sns.scatterplot(x=feature, y='SalePrice', hue='SalePrice', palette='Blues', data=train) plt.xlabel('{}'.format(feature), size=15,labelpad=12.5) plt.ylabel('SalePrice', size=15, labelpad=12.5) for j in range(2): plt.tick_params(axis='x', labelsize=12) plt.tick_params(axis='y', labelsize=12) plt.legend(loc='best', prop={'size': 10})plt.show()

模型训练

模型训练过程中的重要细节

交叉验证：使用12-折交叉验证

模型：在每次交叉验证中，同时训练七个模型（ridge, svr, gradient boosting, random forest, xgboost, lightgbm regressors）

Stacking 方法：使用xgboot训练了元 StackingCVRegressor 学习器

模型融合：所有训练的模型都会在不同程度上过拟合，因此，为了做出最终的预测，将这些模型进行了融合，得到了鲁棒性更强的预测结果

初始化交叉验证，定义误差评估指标

# Setup cross validation foldskf = KFold(n_splits=12, random_state=42, shuffle=True)

# Define error metricsdef rmsle(y, y_pred): return np.sqrt(mean_squared_error(y, y_pred))def cv_rmse(model, X=X): rmse = np.sqrt(-cross_val_score(model, X, train_labels, scoring="neg_mean_squared_error", cv=kf)) return (rmse)

建立模型

# Light Gradient Boosting Regressorlightgbm = LGBMRegressor(objective='regression', num_leaves=6, learning_rate=0.01, n_estimators=7000, max_bin=200, bagging_fraction=0.8, bagging_freq=4, bagging_seed=8, feature_fraction=0.2, feature_fraction_seed=8, min_sum_hessian_in_leaf = 11, verbose=-1, random_state=42)# XGBoost Regressorxgboost = XGBRegressor(learning_rate=0.01, n_estimators=6000, max_depth=4, min_child_weight=0, gamma=0.6, subsample=0.7, colsample_bytree=0.7, objective='reg:linear', nthread=-1, scale_pos_weight=1, seed=27, reg_alpha=0.00006, random_state=42)# Ridge Regressorridge_alphas = [1e-15, 1e-10, 1e-8, 9e-4, 7e-4, 5e-4, 3e-4, 1e-4, 1e-3, 5e-2, 1e-2, 0.1, 0.3, 1, 3, 5, 10, 15, 18, 20, 30, 50, 75, 100]ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=ridge_alphas, cv=kf))# Support Vector Regressorsvr = make_pipeline(RobustScaler(), SVR(C= 20, epsilon= 0.008, gamma=0.0003))# Gradient Boosting Regressorgbr = GradientBoostingRegressor(n_estimators=6000, learning_rate=0.01, max_depth=4, max_features='sqrt', min_samples_leaf=15, min_samples_split=10, loss='huber', random_state=42)# Random Forest Regressorrf = RandomForestRegressor(n_estimators=1200, max_depth=15, min_samples_split=5, min_samples_leaf=5, max_features=None, oob_score=True, random_state=42)# Stack up all the models above, optimized using xgbooststack_gen = StackingCVRegressor(regressors=(xgboost, lightgbm, svr, ridge, gbr, rf), meta_regressor=xgboost, use_features_in_secondary=True)

训练模型

计算每个模型的交叉验证的得分

scores = {}score = cv_rmse(lightgbm)print("lightgbm: {:.4f} ({:.4f})".format(score.mean(), score.std()))scores['lgb'] = (score.mean(), score.std())

lightgbm: 0.1159 (0.0167)

score = cv_rmse(xgboost)print("xgboost: {:.4f} ({:.4f})".format(score.mean(), score.std()))scores['xgb'] = (score.mean(), score.std())

xgboost: 0.1364 (0.0175)

score = cv_rmse(svr)print("SVR: {:.4f} ({:.4f})".format(score.mean(), score.std()))scores['svr'] = (score.mean(), score.std())

SVR: 0.1094 (0.0200)

score = cv_rmse(ridge)print("ridge: {:.4f} ({:.4f})".format(score.mean(), score.std()))scores['ridge'] = (score.mean(), score.std())

ridge: 0.1101 (0.0161)

score = cv_rmse(rf)print("rf: {:.4f} ({:.4f})".format(score.mean(), score.std()))scores['rf'] = (score.mean(), score.std())

rf: 0.1366 (0.0188

score = cv_rmse(gbr)print("gbr: {:.4f} ({:.4f})".format(score.mean(), score.std()))scores['gbr'] = (score.mean(), score.std())

gbr: 0.1121 (0.0164)

拟合模型

print('stack_gen')stack_gen_model = stack_gen.fit(np.array(X), np.array(train_labels))

stack_gen

print('lightgbm')lgb_model_full_data = lightgbm.fit(X, train_labels)

lightgbm

print('xgboost')xgb_model_full_data = xgboost.fit(X, train_labels)

xgboost

print('Svr')svr_model_full_data = svr.fit(X, train_labels)

Svr

print('Ridge')ridge_model_full_data = ridge.fit(X, train_labels)

Ridge

print('RandomForest')rf_model_full_data = rf.fit(X, train_labels)

RandomForest

print('GradientBoosting')gbr_model_full_data = gbr.fit(X, train_labels)

GradientBoosting

融合各个模型，并进行最终预测

# Blend models in order to make the final predictions more robust to overfittingdef blended_predictions(X): return ((0.1 * ridge_model_full_data.predict(X)) + (0.2 * svr_model_full_data.predict(X)) + (0.1 * gbr_model_full_data.predict(X)) + (0.1 * xgb_model_full_data.predict(X)) + (0.1 * lgb_model_full_data.predict(X)) + (0.05 * rf_model_full_data.predict(X)) + (0.35 * stack_gen_model.predict(np.array(X))))

# Get final precitions from the blended modelblended_score = rmsle(train_labels, blended_predictions(X))scores['blended'] = (blended_score, 0)print('RMSLE score on train data:')print(blended_score)

RMSLE score on train data:

0.07537440195302639

各模型性能比较

# Plot the predictions for each modelsns.set_style("white")fig = plt.figure(figsize=(24, 12))ax = sns.pointplot(x=list(scores.keys()), y=[score for score, _ in scores.values()], markers=['o'], linestyles=['-'])for i, score in enumerate(scores.values()): ax.text(i, score[0] + 0.002, '{:.6f}'.format(score[0]), horizontalalignment='left', size='large', color='black', weight='semibold')plt.ylabel('Score (RMSE)', size=20, labelpad=12.5)plt.xlabel('Model', size=20, labelpad=12.5)plt.tick_params(axis='x', labelsize=13.5)plt.tick_params(axis='y', labelsize=12.5)plt.title('Scores of Models', size=20)plt.sho

从上图可以看出，融合后的模型性能最好，RMSE 仅为 0.075，该融合模型用于最终预测。

提交预测结果

# Read in sample_submission dataframesubmission = pd.read_csv("../input/house-prices-advanced-regression-techniques/sample_submission.csv")submission.shape

(1459, 2)

# Append predictions from blended modelssubmission.iloc[:,1] = np.floor(np.expm1(blended_predictions(X_test)))# Fix outleir predictionsq1 = submission['SalePrice'].quantile(0.0045)q2 = submission['SalePrice'].quantile(0.99)submission['SalePrice'] = submission['SalePrice'].apply(lambda x: x if x > q1 else x*0.77)submission['SalePrice'] = submission['SalePrice'].apply(lambda x: x if x < q2 else x*1.1)submission.to_csv("submission_regression1.csv", index=False)

# Scale predictionssubmission['SalePrice'] *= 1.001619submission.to_csv("submission_regression2.csv", index=False)