

射极跟随器电路分析
运算放大器电路
描述
射极跟随器也就是共集电极放大电路,是一种广泛应用的电路。其主要作用是将交流电流放大,以提高整个放大电路的带负载能力。实际电路中,一般用作输出级或隔离级。
其特点为输入阻抗高,输出阻抗低,因而从信号源索取的电流小而且带负载能力强,所以常用于多级放大电路的输入级和输出级;也可用它连接两电路,减少电路间直接相连所带来的影响,起缓冲作用。
射极跟随器电路分析
共发射极放大电路,经推导可得Av=R3/R1,与BJT直流放大系数HFE无关,而是由R3与R1之比来决定的,严格来说是有关系的,但在工程上常可忽略不计。
Figure01
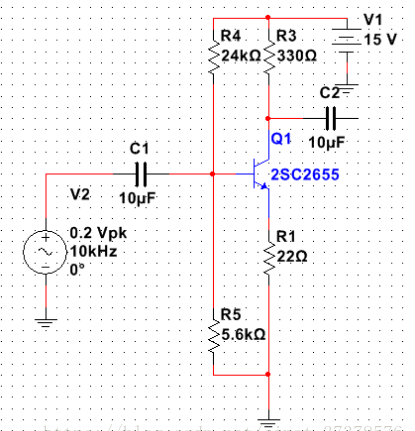
二. 输出阻抗高,为什么共射放大电路的输出阻抗高呢?我们可以实际测量得出,测量的方法如下:(为了便于理解,把figure01简化为figure02,Ro表示输出阻抗,RL为待接负载)
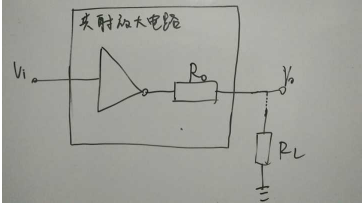
①当共射放大电路输出不接负载时,相当于所接负载RL= ∞,测得此时V0 等于V01=R3/R1*V2=15*0.4=6VPP(V2的峰峰值为0.4V,当RL= ∞时,直接测三极管C极的信号即为这里的V01)
②当接上负载取RL=330Ω 时,可测得输出V02=3VPP=1/2VO1由此可得接上负载后,由于接上负载与共射放大电路的输出阻抗分压作用,导致输出变为1/2V0,即减半,经计算,V02=RL/(RL+Ro)*V01=1/2V01,
⇒RL=Ro=330Ω
⇒Ro=R3=330Ω
⇒共射放大电路的输出阻抗等于集电极电阻R3,这个输出阻抗是很大的,假设后面直接接一个8Ω的扬声器则扬声器两端的电压只有V=8/(330+8)*V01=71MV,信号不仅没有得到放大反而减小,这显然不是我们要的结果,所以这就是接下来我们要介绍的射极跟随器,它的作用就是接在共射放大电路与负载(扬声器)之间,起到阻抗转换的作用,使阻抗降低如到0Ω,从而驱动扬声器发声。
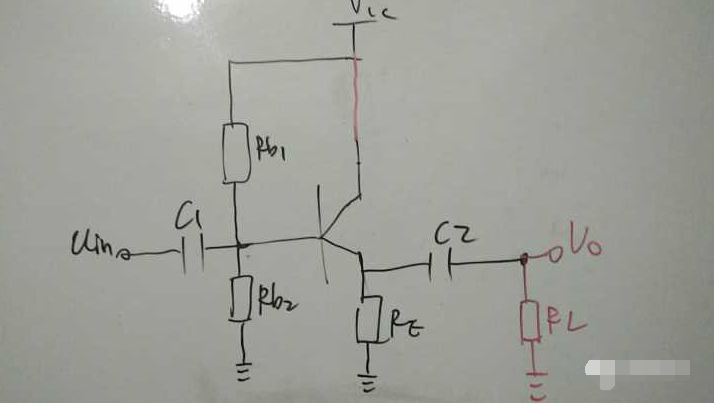
那现在我们先试着搭建射极跟随器的电路,在拿到这个命题时,我们首先应该提前思考这两个问题:
①既然射极跟随器也就是共集电极放大电路,它首先是放大电路,不管是放大电流还是放大电压,既然要起到放大作用,我们首先要给它提供一个使该电路能稳定的工作在放大区的条件,也就是前面教程讲到的提供一个稳定的静态工作点,也就是提供一个偏置电路,以及一个射极反馈电路,使该放大电路的直流特性稳定,不易受温度的影响。
② 既然是射极跟随器,那信号肯定应该从射极取出,因为若从集电极取出的话,那就是共发射极放大电路了,在此加上一个输出时加一个隔直电容,输入仍是基极通过一个耦合电容进行信号输入,最后应该考虑的一点就是集电极应该怎么接了,其实主要纠结点在于是否中间要接一个电阻RC,再接到VCC,来与基极,射极构成发射结正偏,极电结反偏的放大电路。那我们可以讨论一下有没有必要接这个集电极电阻。
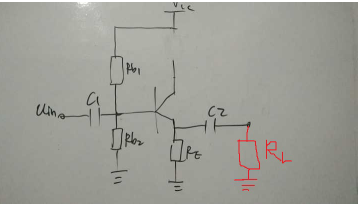
我们前面讲到基极与射极之间存在的一个正偏的PN结,它的直流压差是固定的VBE≈0.6V,而交流阻抗为0,也就是基极输入的交流信号直接短接到射极进行输出,没有任何交流衰减,也就是假设Vb的交流信号为0.4sinwt,那么射极输出的信号也为0.4sinwt,峰峰值不变,而它的直流特性又是VB比VE大0.6V(VB=VE+0.6),根据叠加原理,输入输出信号既有既有直流成分又有交流成分,分别写出基极的信号组成和射极的信号组成
Vb=VB+0.4sinwt.。。.。。.①
Ve=VE+0.4sinwt.。。.。。.②
又VB=VE+0.6待入①中得:
Vb=VE+0.6+0.4sinwt.。。.。。.③
Ve=VE+0.4sinwt.。。.。。.④
我们可以画出③④的波形,figure04可以看出Ve可由Vb往下平移0.6V得到,由③-④得Ve=Vb-0.6V
⇒发射极电位仅由基极Vb来决定而与RE的值、以及Rc的值无关;
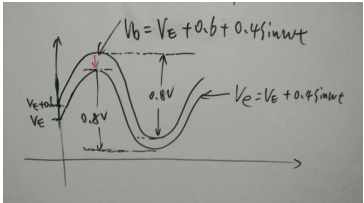
所以我们可以去掉Rc,使集电极直接接VCC,当然如果接上一个Rc电阻的话,电路也能正常工作,但也意味着在该电阻式有额外的功率损耗,因此一般都把Rc省掉。
又因为接在射极跟随器的负载电阻RL,从交流的角度看,是并联接在发射极电阻RE上的,所以改变RL的值与改变RE的值是一样的,如图
figure05
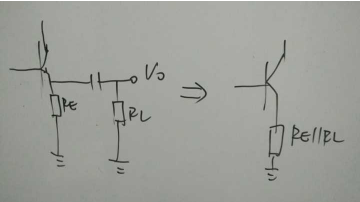
∴Ve交流成分的输出信号V0也与RE的值无关,也就是说即使改变负载电阻的值,输出电压V0=Vi,即可得射极跟随器输出阻抗Ro≈0,为了说明问题我们可以做个实验来验证:
假设我们认为射极跟随器输出阻抗Ro不为0,随便取个值如Ro=8Ω,让负载RL=8Ω,则输出Vo将因为负载分压而减半Vo=RL/(RL+Ro)*Vi=1/2*Vi,而此时我们实际测到的Vo=RL/(RL+Ro)*Vi=1*Vi
⇒RL/(RL+Ro)=1
⇒Ro=0;
与假设矛盾,即假设不成立,
⇒Ro=0;
既然R0=0,也就是说,理论上射极跟随器接的负载为不管为多大时,其输出都跟随输入的值V0=Vi,而不会像前面讲的共发射极放大电路那样被负载拉下来的现象,起到了阻抗变换的作用。
-
射极跟随器的结构和特性2024-10-15 5830
-
射极跟随器的原理 射极跟随器电路图及波形2023-09-11 12109
-
射极跟随电路的参数设计2023-04-21 2256
-
射极跟随器电路设计2023-04-17 14723
-
射极跟随器电路图及波形分析2022-11-11 7696
-
射极跟随器的工作原理及瞬态特性分析2022-10-21 4321
-
射极跟随器的作用是什么2020-06-26 11902
-
射极跟随器有什么性能和特点2018-03-23 81462
-
将射极跟随器接入非门的输入电路2010-03-29 1459
-
射极(源)跟随器,射极(源)跟随器原理是什么2010-03-09 25351
-
射极跟随器原理及应用2010-01-14 2107
-
射极跟随器2009-05-23 5689
-
射极跟随器电路2006-04-15 18222
全部0条评论

快来发表一下你的评论吧 !

